|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Криптографические хэш-функции
Функция сжатия
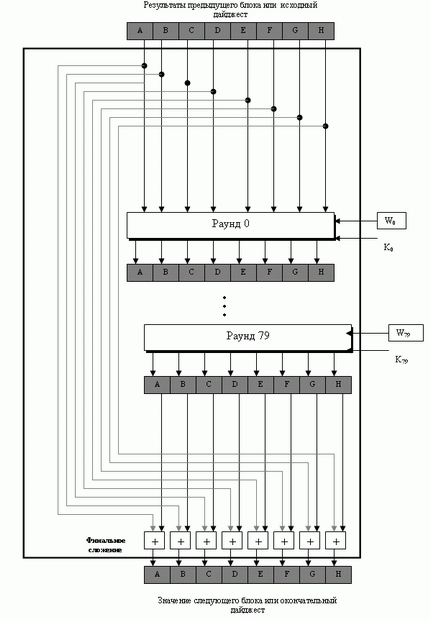
SHA-512 создает 512 битов дайджест-сообщения (восемь слов на 64 бита) из сообщения, которое состоит из множества блоков, где каждый блок содержит 1024 бита. Обработка каждого блока данных в SHA-512 включает 80 раундов. рис. 2.10 показывает общую схему сжатия функции. В каждом раунде содержание восьми предыдущих буферов - это одно слово из расширенного блока ( Wi ), и одна константа на 64 бита ( Ki ), смешанные вместе. Они обработаны затем, чтобы создать новое множество из восьми буферов. В начале обработки значения восьми буферов сохранены как восемь временных переменных. В конце обработки (после того как сделан шаг 79) эти значения добавляются к значениям, созданным на шаге 79. Мы вызываем эту последнюю операцию финальным сложением, как это показано на рисунке.
Структура каждого раунда
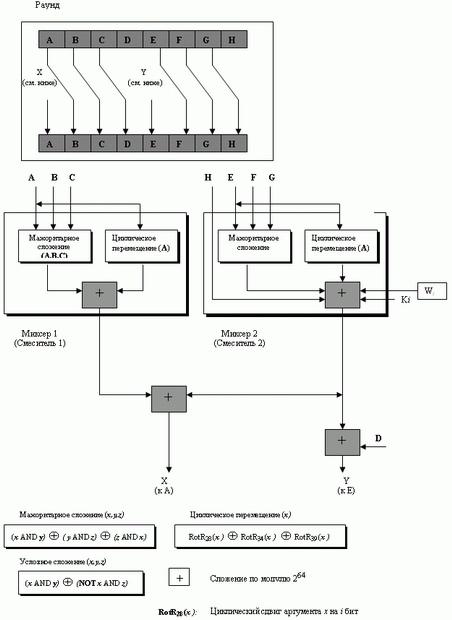
В каждом раунде создаются восемь новых, по сравнению с предыдущим раундом, значений буферов по 64 бита. На рис. 2.11 мы видим, что шесть буферов - точные копии предыдущего раунда, как это показано ниже:
A -> B B -> C C -> D E -> F F -> G G -> H
Два новых буфера, A и E, получают соответствующие значения от некоторых сложных функций, которые включают в себя некоторые значения предыдущих буферов, соответствующее слово для этого раунда (Wi) и константу для этого раунда (Ki). Рис. 2.11 показывает структуру каждого раунда.
Здесь есть два смесителя, три функции и несколько операторов. Каждый смеситель обрабатывает две функции. Описание функций и операторов приведено ниже.
- То, что мы называем мажоритарной функцией, является поразрядной функцией. Она использует три соответствующих бита в трех буферах ( A, B и C ) и вычисляет
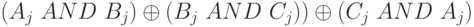
Результат - это значение, которое имеет большинство из трех бит. Если два или три бита равны единице (1) , то результат имеет значение бит 1; иначе он равен 0.
Функция, которую мы называем условной функцией ( Conditional ) - также поразрядная функция. Она использует три бита, которые содержатся в трех буферах ( E, F и G ), и вычисляет
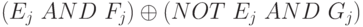
Результат подчиняется логике "Если E, то F ; иначе G ".
- Функция "циклическое перемещение" (Rotate) обрабатывает три значения одного и того же буфера ( A или E ) и применяет операцию ИСКЛЮЧАЮЩЕЕ ИЛИ с результатом мажоритарной функции.
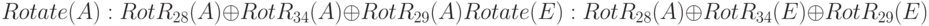
- Функция "циклическое перемещение вправо" (RotRi (x) ) - та же самая, которую мы использовали в процессе расширения слова.
- Оператор сложения, применяемый в процессе, - сложение по модулю 264. Он означает результат сложения двух или больше буферов, содержащих всегда слово на 64 бита.
- Есть 80 констант, K0 к K79, каждая по 64 бита, как показано в табл. 2.3 в шестнадцатеричной форме (четыре в каждой строке таблицы). Аналогично начальным значениям для восьми буферов, эти значения вычислены из первых 80 простых чисел ( 2, 3..., 409 ).
Каждое значение - дробная часть кубического корня из соответствующего простого числа после преобразования этого числа к двоичной форме, сохраняются только первые 64 бита. Например, 80-е простое число - ( 409 ). Кубический корень (409) 1/3 = 7,42291412044. Преобразовывая это число к двоичному виду только с 64 битами в дробной части, мы получаем
(111,0110 1100 0100 0100...0111) 2 -> (7,6C44198C4A475817).
SHA-512 сохраняет дробную часть, (6C44198C4A475817)16, как целое число без знака.
Пример 2.7
Мы применяем мажоритарную функцию к значениям буферов A, B и C. Если крайние левые шестнадцатеричные цифры этих буферов - 0x7, 0xA и 0xE соответственно, то какая цифра будет крайней левой частью результата?
Решение
Цифры в двоичной форме - 0111, 1010 и 1110.
- Первые биты - 0, 1 и 1. Мажоритарная функция равна 1. Мы можем доказать это, используя определение мажоритарной функции:
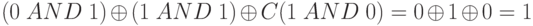
- Вторые биты - 1, 0 и 1. Мажоритарная функция равна 1 .
- Третьи биты - 1, 1 и 1. Мажоритарная функция равна 1.
- Четвертые биты - 1, 0 и 0. Мажоритарная функция равна 0. Результат - 1110, или 0xE в шестнадцатеричной форме.
Пример 2.8
Мы применяем условную функцию ( Conditional ) для буферов E, F и G. Если крайние левые шестнадцатеричные цифры этих буферов - 0x9, 0xE и 0xF соответственно, то какая цифра будет крайней левой частью результата?
Решение
Цифры в двоичной форме - 1001, 1110 и 1111.
- Первые биты - 1,1 и 1. Следовательно, E1 = 1, результат - F1, который равен 1. Чтобы доказать результат, мы можем также использовать определение функции Condition:
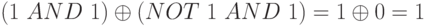
- Вторые биты - 0, 0 и 1. Следовательно, E2 - 0, результат - F3, который равен 1.
- Третьи биты образовывают дугу 0, 1 и 1. Следовательно, E3 - 0, результат - G3, который равен 1.
- Четвертые биты - 1, 0 и 1. Следовательно, E4 - 1, результат - F4, который равен 0. Результат - 1110, или 0x1 в шестнадцатеричной форме.
Анализ
С дайджестом сообщения 512 битов от SHA-512 ожидалось, что он будет более стойким ко всем типам атак, включая атаки коллизии. Он должен был быть лучшим проектом этой версии: более эффективным и более безопасным, чем предыдущие. Однако необходимы были серьезные исследования и испытания, для того чтобы это подтвердить.