Эконометрические методы управления качеством и сертификации продукции

Планы статистического контроля и правила принятия решений. Под планом статистического контроля понимают алгоритм, т.е. правила действий, на входе при этом-генеральная совокупность (партия продукции), а на выходе-одно из двух решений: "принять партию" либо "забраковать партию". Рассмотрим несколько примеров.

Одноступенчатые планы контроля 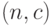: отобрать выборку объема ; если число дефектных единиц в выборке не превосходит , то партию принять, в противном случае забраковать. Число называется приемочным.

Частные случаи: план 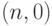-партию принять тогда и только тогда, когда все единицы в выборке являются годными; план 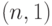- партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется.

Двухступенчатый план контроля 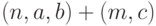: отобрать первую выборку объема ; если число дефектных единиц в первой выборке не превосходит 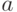, то партию принять; если число дефектных единиц в первой выборке больше или равно , то партию забраковать; во всех остальных случаях, т.е. когда больше , но меньше , следует взять вторую выборку объема ; если число дефектных единиц во второй выборке не превосходит , то партию принять, в противном случае забраковать.

Рассмотрим в качестве примера план 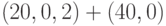. Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют.

В реальной нормативно-технической документации - договорах на поставку, стандартах, технических условиях, инструкциях по экологическому контролю и т.д. - не всегда четко сформулированы планы статистического контроля и правила принятия решений. Например, при описании двухступенчатого плана контроля вместо задания приемочного числа с может стоять загадочная фраза "результат контроля второй выборки считается окончательным". Остается гадать, как принимать решение по второй выборке. Менеджер, администратор (государственный служащий), эколог или экономист, занимающийся вопросами экологического контроля или контроля качества, должен первым делам добиваться кристальной ясности в формулировках правил принятия решений, иначе ошибочные и необоснованные решения, а потому и убытки неизбежны.

Оперативная характеристика плана статистического контроля. Каковы свойства плана статистического контроля? Они, как правило, определяются с помощью функции 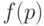, связывающей вероятность дефектности единицы контроля с вероятностью 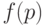положительной оценки экологической обстановки (приемки партии) по результатам контроля. При этом вероятность того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют, , то партия всегда принимается, т.е. . Если все единицы дефектные, , то партия наверняка бракуется, 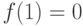. Между этими крайними значениями 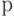функция 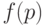монотонно убывает.

Вычислим оперативную характеристику плана 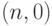. Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица-годная, равна 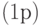, то оперативная характеристика имеет вид

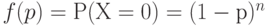( 5)

Для плана 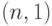оперативная характеристика, как легко видеть, такова:

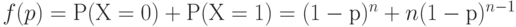( 6)

Оперативные характеристики для конкретных планов статистического контроля не всегда имеют такой простой вид, как в случае формул (5) и (6). Рассмотрим в качестве примера план 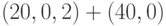. Сначала найдем вероятность того, что партия будет принята по результатам контроля первой партии. Согласно формуле (5) имеем:

Вероятность того, что понадобится контроль второй выборки, равна

При этом вероятность того, что по результатам её контроля партия будет принята, равна

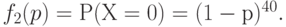
Следовательно, вероятность того, что партия будет принята со второй попытки, т.е. что при контроле первой выборки обнаружится ровно одна дефектная единица, а затем при контроле второй-ни одной, равна

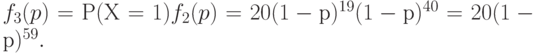
Следовательно, вероятность принятия партии с первой или со второй попытки равна

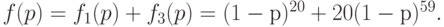
При практическом применении методов статистического приемочного контроля для нахождения оперативных характеристик планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы.

Риск поставщика и риск потребителя, приемочный и браковочный уровни дефектности. С оперативной характеристикой связаны важные понятия приемочного и браковочного уровней дефектности, а также понятия "риск поставщика" и "риск потребителя". Чтобы ввести эти понятия, на оперативной характеристике выделяют две характерные точки, делящие входные уровни дефектности на три зоны- А, Б и В. В зоне А все почти всегда хорошо, а именно - почти всегда экологическая обстановка признается благополучной, почти все партии принимаются. В зоне В, наоборот, почти всегда все плохо, а именно - почти всегда экологический контроль констатирует экологические нарушения, почти все партии бракуются. Зона. Б - буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа-риск поставщика (производителя, предприятия) и риск потребителя (заказчика, системы экологического контроля) , при этом границы между зонами задают два уровня дефектности - приемочный 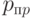и браковочный , определяемые из уравнений

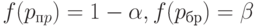( 7)

Таким образом, если входной уровень дефектности не превосходит 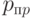, то вероятность забракования партии мала, т.е. не превосходит . Приемочный уровень дефектности выделяет зону значений входного уровня дефектности, в которой нарушения экологической безопасности почти всегда не отмечаются, партии почти всегда принимаются, т.е. соблюдаются интересы проверяемого предприятия (в экологии), поставщика (при контроле качества). Это - зона комфортности для поставщика. Если он обеспечивает работу (уровень дефектности) в этой зоне, то его никто не потревожит.

Если же входной уровень дефектности больше браковочного уровня дефектности , то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне 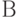соблюдаются интересы потребителей - брак к ним не попадает.

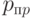При выборе плана контроля часто начинают с выбора приемочного и браковочного уровней дефектности. При этом выбор конкретного значения приемочного уровня дефектности отражает интересы поставщика, а выбор конкретного значения браковочного уровня дефектности - интересы потребителя. Можно доказать, что для любых положительных чисел и , и любых входных уровней дефектности и , причем 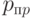меньше , найдется план контроля 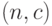такой, что его оперативная характеристика 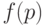удовлетворяет неравенствам

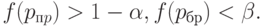
При практических расчетах обычно принимают 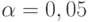(т.е. 5%) и 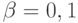(т.е. 10%).

Вычислим приемочный и браковочный уровни дефектности для плана . Из формул (5) и (7) вытекает, что

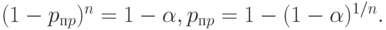
Поскольку риск поставщика мал, то из известного соотношения математического анализа

вытекает приближенная формула

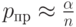
Для браковочного уровня дефектности имеем

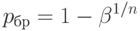
При практическом применении методов статистического приемочного контроля для нахождения приемочных и браковочных уровней дефектности планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы, имеющиеся в нормативно-технической документации или научно-технических публикациях.

Предел среднего выходного уровня дефектности. Обсудим судьбу забракованной партии продукции. В зависимости от ситуации эта судьба может быть разной. Партия может быть утилизирована. Например, забракованная партия гвоздей может быть направлена на переплавку. У партии может быть понижена сортность, и она может быть продана по более низкой цене (при этом результаты выборочного контроля будут использованы не для проверки того, что выдержан заданный уровень качества, а для оценки реального уровня качества). Наконец, партия продукции может быть подвергнута сплошному контролю (для этого обычно привлекают инженеров из всех заводских служб). При сплошном контроле все дефектные изделия обнаруживаются и либо исправляются на месте, либо извлекаются из партии. В результате в партии остаются только годные изделия. Такая процедура называется "контроль с разбраковкой".

При среднем входном уровне дефектности 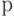и применении контроля с разбраковкой с вероятностью 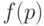партия принимается (и уровень дефектности в ней по-прежнему равен р) и с вероятностью 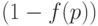бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен

Средний выходной уровень дефектности равен 0 при и , положителен на интервале (0;1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД):

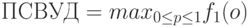
Пример. Рассмотрим план . Для него 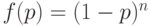и 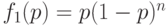. Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:

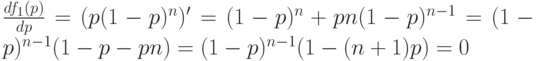
В полученном уравнении корень соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при

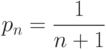
Следовательно,

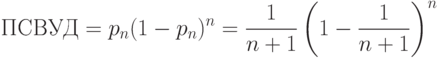( 8)

По выражению (8) могут быть проведены конкретные расчеты. Однако оно довольно громоздко. Его можно упростить, используя один замечательный предел из курса математического анализа, а именно:

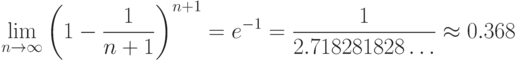( 9)

Сравнивая соотношения (8) и (9), видим, что

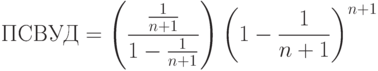
Первая скобка равна 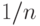, а вторая согласно соотношению (9) приближается к 0,368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу

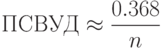
Для более сложных планов ПСВУД рассчитывают с помощью более или менее сложных компьютерных программ.

При рассмотрении основ статистического контроля в настоящем пункте расчетные формулы удалось получить лишь для простейших планов, в основном для планов вида 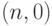. Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при 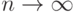, то можно справиться и с одноступенчатыми планами вида .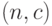