|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Основы эконометрических методов
Асимптотическое распределение прогностической функции. Из формул (5) и (6) следует, что
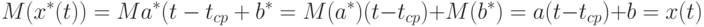
т.е. рассматриваемая оценка прогностической функции является несмещенной. Поэтому
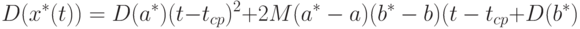
При этом, поскольку погрешности независимы в совокупности и 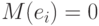 , то
, то
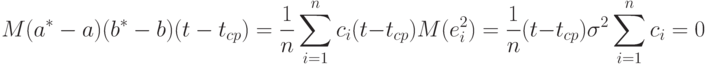
Таким образом,
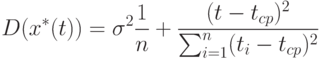
Итак, оценка 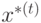 является несмещенной и асимптотически нормальной. Для ее практического использования необходимо уметь оценивать остаточную дисперсию
является несмещенной и асимптотически нормальной. Для ее практического использования необходимо уметь оценивать остаточную дисперсию 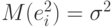
Оценивание остаточной дисперсии. В точках 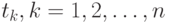 , имеются исходные значения зависимой переменной
, имеются исходные значения зависимой переменной 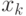 и восстановленные значения
и восстановленные значения 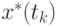 . Рассмотрим остаточную сумму квадратов
. Рассмотрим остаточную сумму квадратов
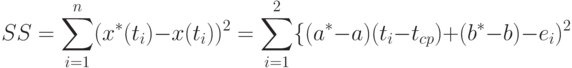
В соответствии с формулами (5) и (6)
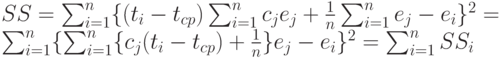
Найдем математическое ожидание каждого из слагаемых:
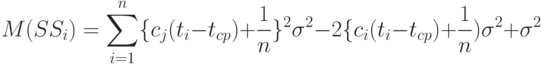
Из сделанных ранее предположений вытекает, что при 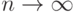 имеем
имеем 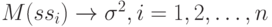 следовательно, по закону больших чисел статистика
следовательно, по закону больших чисел статистика  является состоятельной оценкой остаточной дисперсии
является состоятельной оценкой остаточной дисперсии 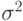 .
.
Получением состоятельной оценкой остаточной дисперсии завершается последовательность задач, связанных с рассматриваемым простейшим вариантом метода наименьших квадратов. Не представляет труда выписывание верхней и нижней границ для прогностической функции:
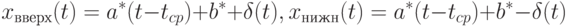
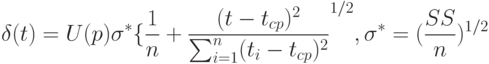
Здесь  - доверительная вероятность,
- доверительная вероятность, 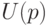 , как и в главе 4 - квантиль нормального распределения порядка
, как и в главе 4 - квантиль нормального распределения порядка 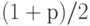 , т.е.
, т.е.
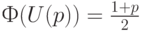
При 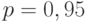 (наиболее применяемое значение) имеем
(наиболее применяемое значение) имеем  . Для других доверительных вероятностей соответствующие значения квантилей можно найти в статистических таблицах .
. Для других доверительных вероятностей соответствующие значения квантилей можно найти в статистических таблицах .
Сравнение параметрического и непараметрического подходов. Во многих литературных источниках рассматривается параметрическая вероятностная модель метода наименьших квадратов. В ней предполагается, что погрешности имеют нормальное распределение. Это предположение позволяет математически строго получить ряд выводов. Так, распределения статистик вычисляются точно, а не в асимптотике, соответственно вместо квантилей нормального распределения используются квантили распределения Стьюдента, а остаточная сумма квадратов  делится не на
делится не на  , а на
, а на 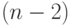 . Ясно, что при росте объема данных различия стираются.
. Ясно, что при росте объема данных различия стираются.
Рассмотренный выше непараметрический подход не использует нереалистическое предположение о нормальности погрешностей. Распределения, встречающиеся в задачах менеджмента, как правило, не являются нормальными. Платой за отказ от нормальности является асимптотический характер результатов. В случае простейшей модели метода наименьших квадратов оба подхода дают практически совпадающие рекомендации. Это не всегда так, не всегда два подхода бают близкие результаты. Например, в задаче обнаружения выбросов методы, опирающиеся на нормальное распределение, нельзя считать обоснованными, и обнаружено это было с помощью непараметрического подхода.
Общие принципы. Кратко сформулируем несколько общих принципов построения, описания и использования эконометрических методов анализа данных. Во-первых, должны быть четко сформулированы исходные предпосылки, т.е. полностью описана используемая вероятностно-статистическая модель. Во-вторых, не следует принимать предпосылки, которые редко выполняются на практике. В-третьих, алгоритмы расчетов должны быть корректны с точки зрения математико-статистической теории. В-четвертых, алгоритмы должны давать полезные для практики выводы.
Применительно к задаче восстановления зависимостей это означает, что целесообразно применять непараметрический подход, что и сделано выше.
Пример оценивания по методу наименьших квадратов. Пусть даны  пар чисел
пар чисел 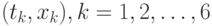 , представленных во втором и третьем столбцах табл.13.1. В соответствии с формулами (2) и (4) выше для вычисления оценок метода наименьших квадратов достаточно найти суммы выражений, представленных в четвертом и пятом столбцах табл.13.1.
, представленных во втором и третьем столбцах табл.13.1. В соответствии с формулами (2) и (4) выше для вычисления оценок метода наименьших квадратов достаточно найти суммы выражений, представленных в четвертом и пятом столбцах табл.13.1.
 |
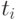 |
 |
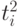 |
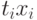 |
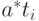 |
 |
 |
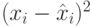 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 12 | 1 | 12 | 3,14 | 12,17 | -0,17 | 0,03 |
| 2 | 3 | 20 | 9 | 60 | 9,42 | 18,45 | 1,55 | 2,40 |
| 3 | 4 | 20 | 16 | 80 | 12,56 | 21,59 | -1,59 | 2,53 |
| 4 | 7 | 32 | 49 | 224 | 21,98 | 31,01 | 0,99 | 0,98 |
| 5 | 9 | 35 | 81 | 315 | 28,26 | 37,29 | -2,29 | 5,24 |
| 6 | 10 | 42 | 100 | 420 | 31,40 | 40,43 | 1,57 | 2,46 |
 |
34 | 161 | 256 | 1111 | 0,06 | 13,64 | ||
 |
5,67 | 26,83 | 42,67 | 185,17 |
В соответствии с формулой (2) 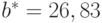 , а согласно формуле (4)
, а согласно формуле (4)
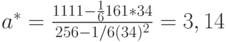
Следовательно, прогностическая формула имеет вид
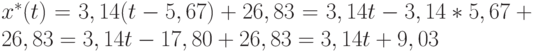
Следующий этап анализа данных - оценка точности приближения функции методом наименьших квадратов. Сначала рассматриваются т.н. восстановленные значения

Это те значения, которые полученная в результате расчетов прогностическая функция принимает в тех точках, в которых известны истинные значения зависимой переменной 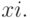

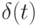 имеет вид
имеет вид