|
Reference = add reference, в висуал студия 2010 не могу найти в вкладке Solution Explorer, Microsoft.Xna.Framework. Его нету. |
Визуализация примитивов
Практическое упражнение №2.3
Напишите приложение, рисующее обыкновенный деревянный забор, покрашенный (рисунок 2.28). Готовое приложение находится в ![]() example.zip в каталоге Ch02\Ex14.
example.zip в каталоге Ch02\Ex14.
2.6.2. Веер треугольников (PrimitiveType.TriangleFan)
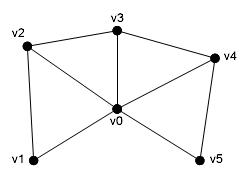
Следующий тип примитивов, PrimitiveType.TriangleFan, используется для рисования вееров треугольников. Первые три вершины (0-я, 1-я и 2-я) задают первый треугольник. Второй треугольник задается 0-й, 2-й и 3-й вершинами, третий – 0-й, 3-й и 4-й вершинами и т.д. (рисунок 2.29). Данный тип примитивов идеально подходит для рисования эллипсов, окружностей, секторов окружностей и аналогичных фигур.
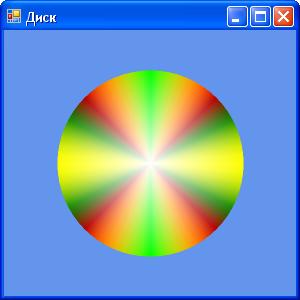
Чтобы опробовать этот тип примитива на практике, мы модифицируем пример Ex09, заставив его рисовать на экране закрашенный круг вместо окружности (рисунки 2.31). Для этого придется внести три небольших изменения в обработчики событий Load и Paint:
- Увеличить размер массива вершин на одну вершину.
- Вставить в начало массива вершину с координатами центра окружности
- Изменить тип примитива с LineList на TriangleFan
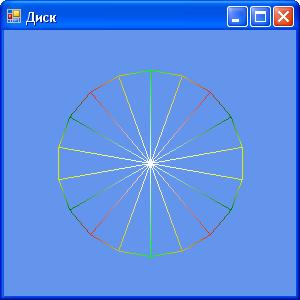
Так же мы добавим в программу возможность переключения между каркасным и закрашенным режимами отображения треугольников при помощи клавиши пробел ( Space ). Эта функциональность, позволяющая просматривать топологию сцены, неоценима при отладке приложения (рисунок 2.31).
Основные фрагменты исходного кода полученного приложения ( Ex15 ) приведены в листинге 2.25.
// Количество сегментов в круге
const int slices = 64;
// Режим закраски круга
FillMode fillMode = FillMode.Solid;
private void MainForm_Load(object sender, EventArgs e)
{
...
// Создаем графический буфер
vertices = new VertexPositionColor[slices + 2];
// Помещаем в начало графического буфера
вершину, расположенную в центре экрана
vertices[0] = new VertexPositionColor(new Vector3(0.0f, 0.0f, 0.0f),
XnaGraphics.Color.White);
// Перебираем все вершины окружности for (int i = 0;
i <= slices; i++)
{
// Определяем координаты текущей вершины
float angle = (float)i /
(float)slices * 2.0f * (float)Math.PI; float x = 0.7f *
(float)Math.Sin(angle); float y = 0.7f * (float)Math.Cos(angle);
// Вычисляем цвет вершины
byte red = (byte)(255 * Math.Abs(Math.Sin(angle * 3))); byte green =
(byte)(255 * Math.Abs(Math.Cos(angle * 2)));
// Помещаем информацию о вершине в массив вершин
vertices[i + 1] = new VertexPositionColor(new Vector3(x, y, 0.0f), new
XnaGraphics.Color(red, green, 0)); }; ... }
private void MainForm_Paint(object sender, PaintEventArgs e)
{
...
// Задаем область визуализации размером во весь
экран. Для вычисления параметров видового
// преобразования используется метод
FullScreenViewport нашего вспомогательного класса Helper
device.Viewport = Helper.FullScreenViewport(ClientSize);
// Закрашиваем поверхность формы
device.Clear(XnaGraphics.Color.CornflowerBlue);
// Задаем квадратную область закраски максимально
возможного размера device.Viewport = Helper.SquareViewport(ClientSize);
// Выключаем отсечение треугольников (см. предыдущий раздел)
device.RenderState.CullMode = CullMode.None;
// Задаемрежим визуализации треугольников
device.RenderState.FillMode = fillMode;
device.VertexDeclaration = decl;;
// Рисуем круг
effect.Begin();
foreach (EffectPass pass in effect.CurrentTechnique.Passes)
{
pass.Begin();
device.DrawUserPrimitives(PrimitiveType.
TriangleFan, vertices, 0, vertices.Length - 2);
pass.End(); } effect.End();
// Переключаем вспомогательные буферы
device.Present(); }
// Обработчик события нажатия клавиш
private void MainForm_KeyDown(object sender, KeyEventArgs e)
{
// Если нажата клавиша пробел
if (e.KeyCode == Keys.Space)
{
// Меняем режим отображения
if (fillMode == FillMode.Solid)
fillMode = FillMode.WireFrame; else
fillMode = FillMode.Solid;
// Обновляем изображение Invalidate();
}
}
Листинг
2.25.
2.6.3.Полоса из связанных треугольников (PrimitiveType.TriangleStrip)
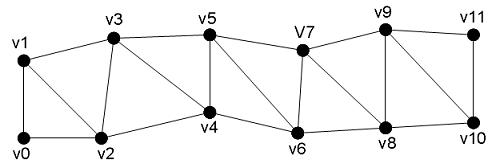
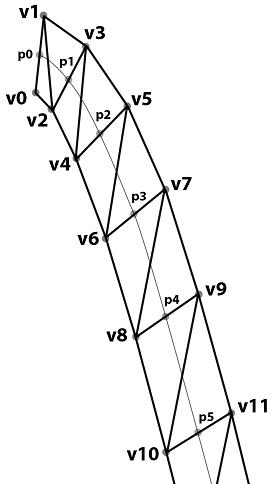
Последний тип примитивов, PrimitiveType.TriangleStrip, предназначен для рисования полосы из связанных треугольников. При этом первый треугольник проходит через 0-ю, 1-ю 2-ю вершины, второй треугольник – через 3-ю, 2-ю и 1-ю вершины, третий треугольник – через 2-ю, 3-ю и 4-ю вершины, четвертый через 5-ю, 4-ю и 3-ю, и т.д (рисунок 2.32). Обратите внимание на порядок перечисления вершин в треугольниках: все треугольники в полосе имеют одинаковую ориентацию относительно часовой стрелки – например, если вершины первого треугольника располагаются по часовой стрелке, то и вершины других треугольников так же будут перечисляться по часовой стрелке. Эта особенность используется при отсечении невидимых треугольников с использованием поля RenderState.CullMode.
Данный тип примитивов очень удобно использовать для визуализации ломаных линий шириной больше одного пикселя, то есть в качестве продвинутой версии примитива PrimitiveType.LineStrip. В частности, на рисунке 2.32 в качестве иллюстрации приведена ломаная линия переменной ширины, состоящая из пяти сегментов.
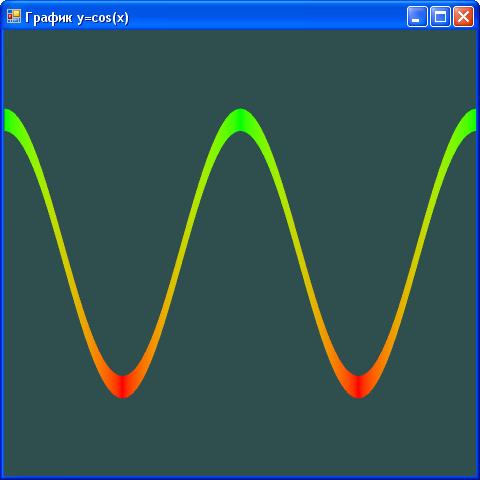
Визуализация графика функции y=cos(x)
Чтобы попрактиковаться в рисовании ломаных линий при помощи примитива PrimitiveType.TriangleStrip, мы напишем приложение, визуализирующее график косинуса в интервале с 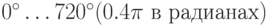 использованием ломаной толщиной 10 пикселей. Хотя на первый взгляд эта задача не намного сложнее практический упражнений №2.1 и №2.2, она все же имеет несколько подвохов.
использованием ломаной толщиной 10 пикселей. Хотя на первый взгляд эта задача не намного сложнее практический упражнений №2.1 и №2.2, она все же имеет несколько подвохов.
Для начала сформулируем задачу более четко. Нам необходимо построить полосу из связанных треугольников, аппроксимирующую график косинуса, центр которой совпадает с графиком косинуса (рисунок 2.33).
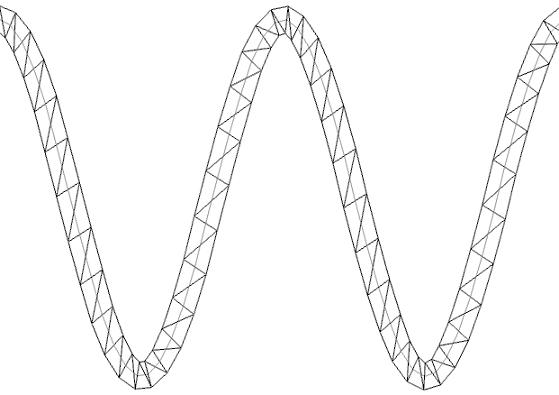
Рис. 2.33. Полоса из связанных треугольников, аппроксимирующая график косинуса (тонкая линию, проходящая по центру полосы).
Для построения синусоиды мы будем перебирать точки графика косинуса с определенным шагом. На рисунке 2.30 эти точки обозначены как 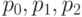 и т.д. Отступив симметрично по обе стороны от точки p0 на некоторое расстояние, например, на 0.05 единиц, мы получим две вершины
и т.д. Отступив симметрично по обе стороны от точки p0 на некоторое расстояние, например, на 0.05 единиц, мы получим две вершины 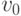 и
и 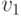 , расстояние межу которыми равно 10 пикселей. Проделав аналогичную операцию над остальными точками, мы получим пары вершин (
, расстояние межу которыми равно 10 пикселей. Проделав аналогичную операцию над остальными точками, мы получим пары вершин ( 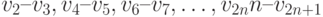 ), расстояние между которыми равно 0.1 единиц. И, наконец, построив полосу из треугольников, опирающуюся на вершины
), расстояние между которыми равно 0.1 единиц. И, наконец, построив полосу из треугольников, опирающуюся на вершины 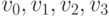 , мы получим ломаную линию толщиной 0.1 пикселей, точно аппроксимирующую график косинуса (рисунок 2.34).
, мы получим ломаную линию толщиной 0.1 пикселей, точно аппроксимирующую график косинуса (рисунок 2.34).
По ширине график косинуса будет вписан в клиентскую область окна, а по высоте наш график будет немного меньше высоты окна. Таким образом, в действительности наше приложение будет визуализировать не сам график 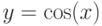 , а несколько другую функцию, полученную путем масштабирования графика
, а несколько другую функцию, полученную путем масштабирования графика 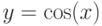 вдоль осей X и Y:
вдоль осей X и Y:
 |
( 2.9) |
где
-
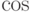 - функция вычисляющая значение косинуса в радианах
- функция вычисляющая значение косинуса в радианах -
 - аргумент функции, лежащий в диапазоне [-1, +1] . Фактически это координата x графика, пробегающая с определенным шагом значения от левого до правого краев экрана, то есть от -1 до +1. Соответственно аргумент функции косинуса пробегает значения от 0 до 4 • 71 (0°...720°).
- аргумент функции, лежащий в диапазоне [-1, +1] . Фактически это координата x графика, пробегающая с определенным шагом значения от левого до правого краев экрана, то есть от -1 до +1. Соответственно аргумент функции косинуса пробегает значения от 0 до 4 • 71 (0°...720°). -
 - координата у графика функции, лежащая в диапазоне от [-0.7, +0.7] .
- координата у графика функции, лежащая в диапазоне от [-0.7, +0.7] .
Перебирая с определенным шагом значения координаты X от -1 до +1 и подставляя их в выражение (2.9), мы получим координаты набора точек 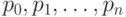 (рисунок 2.34). Как говорилось выше, для получения координат вершин полосы треугольников
(рисунок 2.34). Как говорилось выше, для получения координат вершин полосы треугольников 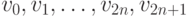 необходимо симметрично отупить от точек
необходимо симметрично отупить от точек  на 0.05 единиц.
на 0.05 единиц.
Вроде бы все просто и понятно, если не считать одной мелочи: мы пока не еще определились, каким образом должны быть сориентированы отрезки 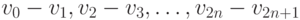 относительно точек
относительно точек 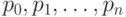 . Не мудрствуя лукаво, мы сделаем эти отрезки параллельными оси Y и посмотрим, что из этого выйдет:
. Не мудрствуя лукаво, мы сделаем эти отрезки параллельными оси Y и посмотрим, что из этого выйдет:
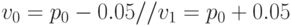 |
( 2.10) |
и т.д.
Основные фрагменты приложения (Ex16) приведены в листинге 2.26.
public partial class MainForm : Form
{
// Количество сегментов в ломаной линии,
аппроксимирующей график косинуса
const int QuadStrips = 100;
// Число треугольников в ломанной линии
const int TriStrips = QuadStrips * 2;
// Массив вершин
VertexPositionColor[] vertices = null;
// Режим закраски треугольников
FillMode fillMode = FillMode.Solid;
private void MainForm_Load(object sender, EventArgs e)
{ ...
// Создаем массив вершин для хранения вершин
полоски из треугольников vertices = new
пVertexPositionColor[TriStrips+2];
// Перебираем вершины полоски из треугольников
for (int i = 0; i <= QuadStrips; i++)
{
// Определяем текущее значение координаты x вершины
float x = -1.0f + 2.0f * (float) i / (float) QuadStrips;
// Вычисляем значение косинуса, соответствующее координате x
float angle = 2.0f * (float)Math.PI * x;
float cos = (float)Math.Cos(angle);
// Вычисляем значение координаты y вершины по формуле 2.9
float y = 0.6f * cos;
// Вычисляем красную и зеленую составляющую
цвета по формулам 2.3 (см. практическое
// упражнение 2.2)
byte green = (byte)(Math.Pow(0.5f + cos * 0.5f, 0.3f) * 255.0f);
byte red = (byte)(Math.Pow(0.5f - cos * 0.5f, 0.3f) * 255.0f);
// Заносим в массив координаты вершины v[i*2] (см. выражение 2.10)
vertices[i * 2] = new VertexPositionColor(new
Vector3(x, y - 0.05f, 0.0f), new
XnaGraphics.Color(red, green, 0));
// Заносим в массив координаты вершины v[i*2+1]
vertices[i * 2 + 1] = new VertexPositionColor
(new Vector3(x, y + 0.05f, 0.0f), new
XnaGraphics.Color(red, green, 0));
};
}
private void MainForm_Paint(object sender, PaintEventArgs e) {
device.Clear(XnaGraphics.Color.DarkSlateGray);
// Выключаем отсечение невидимых треугольников
device.RenderState.CullMode = CullMode.None;
// Задаем режим показа треугольников
device.RenderState.FillMode = fillMode;
device.VertexDeclaration = decl;
// Визуализируем полоску из треугольников,
аппроксимирующую график косинуса effect.Begin();
foreach (EffectPass pass in effect.CurrentTechnique.Passes)
{
pass.Begin();
device.DrawUserPrimitives(PrimitiveType.TriangleStrip, vertices, 0,
vertices.Length - 2);
pass.End();
} effect.End();
device.Present();
}
}
Листинг
2.26.
Скомпилируйте и запустите приложение на выполнение. Как и ожидалось, на экране появится график функции y=cos(x) , однако толщина графика будет переменной, причем максимальная толщина графика будет достигаться в окрестностях точек, в которых функция cos(x) принимает значения -1 или 1. (рисунок 2.35).
Примечание
Следующий материал этого раздела содержит довольно много математических выкладок, поэтому если вы не в ладах с математикой, можете смело пропустить оставшуюся часть раздела 2.6.3.
График y=cos(x) постоянной толщины
И так, попытка использования отрезков 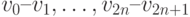 параллельных оси Y закончилась неудачей. Ну что ж, отрицательный результат, это тоже результат. Попробуем поэкспериментировать ориентацией отрезков
параллельных оси Y закончилась неудачей. Ну что ж, отрицательный результат, это тоже результат. Попробуем поэкспериментировать ориентацией отрезков 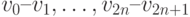 , например, развернув их под углом 45° (рисунок 2.36):
, например, развернув их под углом 45° (рисунок 2.36):
// Вычисляем вектор смещения вершин v[2*i+1] относительно p[n] float nx = (float) (5.0 / Math.Sqrt(2.0)); float ny = nx; // Симметрично смещаем вершины на 5 пикселей в направлении векторов (-1, -1) и (+1, +1) vertices[i * 2] = new VertexPositionColor (new Vector3(x - nx, y - ny, 0.0f), new XnaGraphics.Color(red, green, 0)); vertices[i * 2 + 1] = new VertexPositionColor(new Vector3(x + nx, y + ny, 0.0f), new XnaGraphics.Color(red, green, 0));
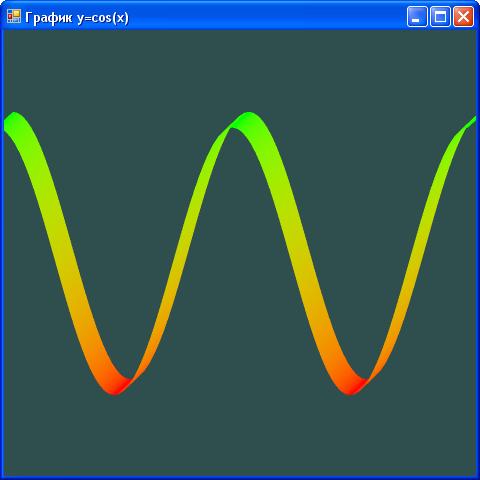
Рис. 2.36. График функции y=cos(x) переменной толщины. Вершины смещаются в направлении векторов (-1, -1) и (+1, +1)
Проведя несколько экспериментов, мы придем к выводу, что график косинуса имеет необходимую толщину только в там, где отрезки 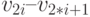 перпендикулярны графику косинуса. Следовательно, чтобы график функции имел постоянную толщину 0.1 единиц, все отрезки
перпендикулярны графику косинуса. Следовательно, чтобы график функции имел постоянную толщину 0.1 единиц, все отрезки 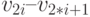 должны быть перпендикулярны графику косинуса.
должны быть перпендикулярны графику косинуса.
Для нахождения координат вершин отрезка 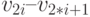 длиной 0.1 единиц, проходящего через точку
длиной 0.1 единиц, проходящего через точку 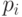 , перпендикулярно графику функции необходимо выполнить следующие действия:
, перпендикулярно графику функции необходимо выполнить следующие действия:
- Найти вектор, s перпендикулярный графику функции в точке pi.
- Найти вектор, параллельный вектору
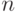 длиной пять единиц, параллельный вектору
длиной пять единиц, параллельный вектору  .
. - Для нахождения координат вершин
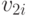 и
и 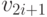 необходимо отложить от точки pi вектора
необходимо отложить от точки pi вектора 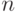 и
и  .
.
Рассмотрим эти шаги более подробно. Как вы знаете из курса аналитической геометрии, вектор, перпендикулярного графику функции, определяются по формуле:
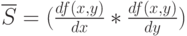 |
( 2.11) |
где
-
 - вектор, перпендикулярный графику функции
- вектор, перпендикулярный графику функции -
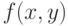 - функция, заданная в неявной форме
- функция, заданная в неявной форме 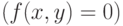 .
. -
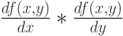 - частные производные по xи y
- частные производные по xи y
Чтобы определить значение вектора s для нашей функции (2.9), перепишем ее в неявной форме 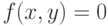 :
:
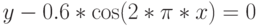 |
( 2.12) |
Теперь найдем частные производные, являющиеся координатами вектора 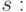
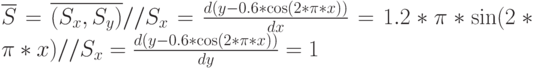 |
( 2.13) |