|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Сетевое планирование и управление
2.1. Теоретический курс
2.1.1. Структурное планирование
Структурное планирование включает в себя несколько этапов:
- разбиение проекта на совокупность отдельных работ, выполнение которых необходимо для реализации проекта;
- построение сетевого графика, описывающего последовательность выполнения работ;
- оценка временных характеристик работ и анализ сетевого графика.
Основную роль на этапе структурного планирования играет сетевой график.
Сетевой график – это ориентированный граф, в котором вершинами обозначены работы проекта, а дугами – временные взаимосвязи работ.
Сетевой график должен удовлетворять следующим свойствам.
- Каждой работе соответствует одна и только одна вершина. Ни одна работа не может быть представлена на сетевом графике дважды. Однако любую работу можно разбить на несколько отдельных работ, каждой из которых будет соответствовать отдельная вершина графика.
- Ни одна работа не может быть начата до того, как закончатся все непосредственно предшествующие ей работы. То есть если в некоторую вершину входят дуги, то работа может начаться только после окончания всех работ, из которых выходят эти дуги.
- Ни одна работа, которая непосредственно следует за некоторой работой, не может начаться до момента ее окончания. Другими словами, если из работы выходит несколько дуг, то ни одна из работ, в которые входят эти дуги, не может начаться до окончания этой работы.
- Начало и конец проекта обозначены работами с нулевой продолжительностью. Такие работы называются вехами и обозначают начало или конец наиболее важных этапов проекта.
Пример. В качестве примера рассмотрим проект "Разработка программного комплекса". Предположим, что проект состоит из работ, характеристики которых приведены в табл.2.1.
| Номер работы | Название работы | Длительность |
|---|---|---|
| 1 | Начало реализации проекта | 0 |
| 2 | Постановка задачи | 10 |
| 3 | Разработка интерфейса | 5 |
| 4 | Разработка модулей обработки данных | 7 |
| 5 | Разработка структуры базы данных | 6 |
| 6 | Заполнение базы данных | 8 |
| 7 | Отладка программного комплекса | 5 |
| 8 | Тестирование и исправление ошибок | 10 |
| 9 | Составление программной документации | 5 |
| 10 | Завершение проекта | 0 |
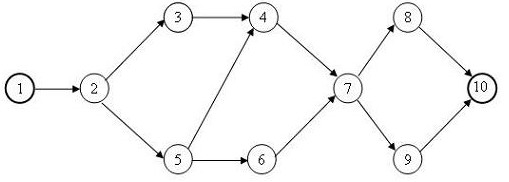
Сетевой график для данного проекта изображен на рис.2.1. На нем вершины, соответствующие обычным работам, обведены тонкой линией, а толстой линией обведены вехи проекта.
Сетевой график позволяет по заданным значениям длительностей работ найти критические работы проекта и его критический путь.
Критической называется такая работа, для которой задержка ее начала приведет к задержке срока окончания проекта в целом. Такие работы не имеют запаса времени. Некритические работы имеют некоторый запас времени, и в пределах этого запаса их начало может быть задержано.
Критический путь – это путь от начальной к конечной вершине сетевого графика, проходящий только через критические работы. Суммарная длительность работ критического пути определяет минимальное время реализации проекта.
Нахождение критического пути сводится к нахождению критических работ и выполняется в два этапа.
- Вычисление раннего времени начала каждой работы проекта. Эта величина показывает время, раньше которого работа не может быть начата.
- Вычисление позднего времени начала каждой работы проекта. Эта величина показывает время, позже которого работа не может быть начата без увеличения продолжительности всего проекта.
Критические работы имеют одинаковое значение раннего и позднего времени начала.
Обозначим 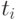 – время выполнения работы
– время выполнения работы  ,
, 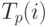 – раннее время начала работы
– раннее время начала работы  ,
, 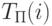 – позднее время начала работы
– позднее время начала работы  . Тогда
. Тогда

где  – множество работ, непосредственно предшествующих работе
– множество работ, непосредственно предшествующих работе  . Раннее время начальной работы проекта принимается равным нулю.
. Раннее время начальной работы проекта принимается равным нулю.
Поскольку последняя работа проекта – это веха нулевой длительности, раннее время ее начала совпадает с длительностью всего проекта. Обозначим эту величину  . Теперь
. Теперь  принимается за позднее время начала последней работы, а для остальных работ позднее время начала вычисляется по формуле:
принимается за позднее время начала последней работы, а для остальных работ позднее время начала вычисляется по формуле:

Здесь  – множество работ, непосредственно следующих за работой
– множество работ, непосредственно следующих за работой  .
.
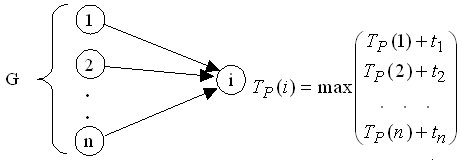
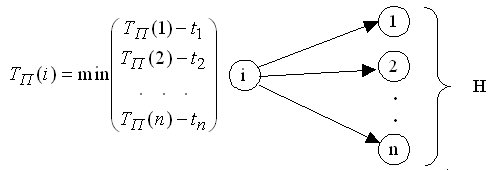
Схематично вычисления раннего и позднего времени начала изображены, соответственно, на рис. 2.2 и рис.2.3.
Пример. Найдем критические работы и критический путь для проекта "Разработка программного комплекса", сетевой график которого изображен на рис.2.1, а длительности работ исчисляются днями и заданы в табл.2.1.
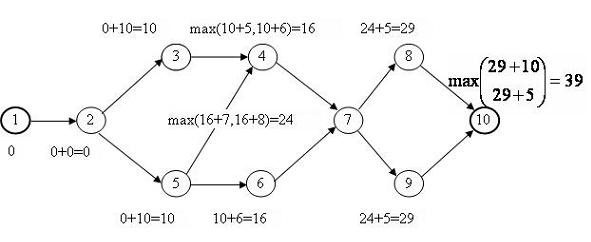
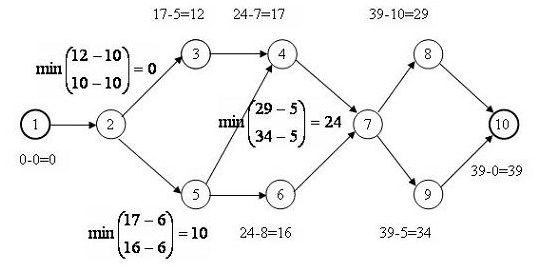
Сначала вычисляем раннее время начала каждой работы. Вычисления начинаются от начальной и заканчиваются конечной работой проекта. Процесс и результаты вычислений изображены на рис.2.4.
Результатом первого этапа помимо раннего времени начала работ является общая длительность проекта  .
.
На следующем этапе вычисляем позднее время начала работ. Вычисления начинаются в последней и заканчиваются в первой работе проекта. Процесс и результаты вычислений изображены на рисунке 2.5.
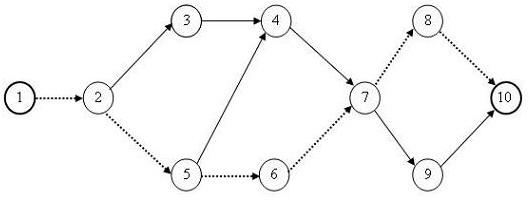
Сводные результаты расчетов приведены в табл.2.2. В ней выделены заливкой критические работы. Критический путь получается соединением критических работ на сетевом графике. Он показан пунктирными стрелками на рис.2.6.
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 10 | 16 | 10 | 16 | 24 | 29 | 29 | 39 |
| Позднее время начала | 0 | 0 | 12 | 17 | 10 | 16 | 24 | 29 | 34 | 39 |
| Резерв времени | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 5 | 0 |
После вычисления величин 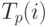 и
и 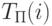 для каждой работы вычисляется резерв времени
для каждой работы вычисляется резерв времени 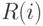 :
:

Эта величина показывает, насколько можно задержать начало работы  без увеличения длительности всего проекта.
без увеличения длительности всего проекта.
Для критических работ резерв времени равен нулю. Поэтому усилия менеджера проекта должны быть направлены в первую очередь на обеспечение своевременного выполнения этих работ.
Для некритических работ резерв времени больше нуля, что дает менеджеру возможность маневрировать временем их начала и используемыми ими ресурсами. Возможны такие варианты.
- Задержка начала работы на величину, не превышающую резерв времени, а требуемые для работы ресурсы направляются для выполнения работ критического пути. Это может дать уменьшение длительности критической работы и проекта в целом;
- Недогрузка некритической работы ресурсами. В результате длительность ее увеличивается в пределах резерва времени, а освободившийся ресурс задействуется для выполнения критической работы, что также приведет к уменьшению длительности ее и всего проекта.
В приведенном примере проекте работы 3, 4 и 9 имеют резерв времени согласно табл.2.2.