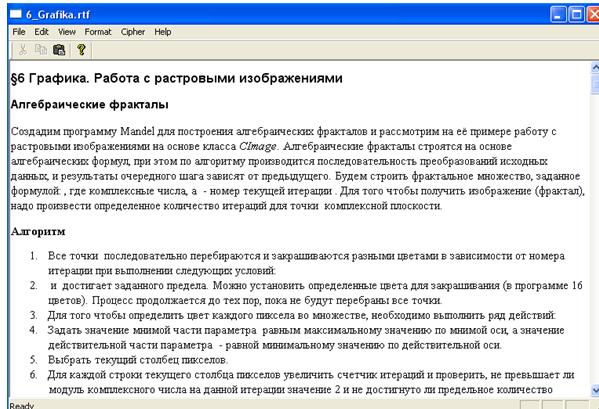
НОУ ИНТУИТ | Программирование под Windows в среде Visual C++ 2005. Лекция 5: Разработка полноценных Windows-приложений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 10.03.2009 | Доступ: свободный | Студентов: 2295 / 280 | Оценка: 4.31 / 4.07 | Длительность: 09:23:00

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 17 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

4. Вывод результатов и их сохранение

Описание вывода результатов частично затронуто в предыдущем пункте. Теперь рассмотрим вывод форматированного текста в файл. Для этого создадим пункт меню File $\to$ Save as…, и обработаем нажатие на него. Но прежде добавим в файл ChildView.h строку:

protected:
  static DWORD CALLBACK FileStreamOutCallback(DWORD dwCookie, LPBYTE pbBuf, LONG cb, LONG *pcb);  
    //Функция обратного вызова для записи данных в файл

и определим объявленный метод в файле ChildView.cpp:

DWORD CALLBACK CChildView::FileStreamOutCallback(DWORD dwCookie, 
  LPBYTE pbBuf, LONG cb, LONG *pcb)
{
  CFile *pFile = (CFile*) dwCookie;
  pFile->Write(pbBuf,cb);
  *pcb = cb;
  return 0;
}

Обработчик пункта меню File $\to$ Save as…

void CChildView::OnFileSaveas()
{
  CString strFilter;  //Строка для поддерживаемых форматов данных
  CString strFileName;  //Строка для имени файла
  CString strExtension;  //Строка для расширения файла

  strFilter = "Text file|*.txt|Rich text format file|*.rtf||";  //Инициализация строки поддерживаемыми форматами
  CFileDialog dlg(FALSE,NULL,NULL,OFN_HIDEREADONLY|OFN_OVERWRITEPROMPT|OFN_EXPLORER,strFilter);  
   //Создание диалога сохранения
  if(dlg.DoModal() == IDOK)  //Если нажата кнопка Ok
  {
  strFileName = dlg.m_ofn.lpstrFile;  //Инициализируем строку с именем файла
  if (dlg.m_ofn.nFileExtension == 0)  //Если пользователь не ввел расширение
  {
  switch (dlg.m_ofn.nFilterIndex)  //В зависисмости от выбранного формата
  {
    case 1: strExtension = "txt"; break;  //Инициализируем строку 
    case 2: strExtension = "rtf"; break;  //с расширением
    default: break;
  }
  strFileName = strFileName + '.' + strExtension;  //Окончательно записываем путь имя и расширение файла
  }
  EDITSTREAM es;  //Создаем структуру потока
  CFile OutFile(strFileName,CFile::modeCreate|CFile::modeWrite);  //Открываем файл для записи
  es.dwCookie = (DWORD) &OutFile;  //Определяем поле структуры, указывающее куда записывать данные
  es.pfnCallback = FileStreamOutCallback;  //Задаем функцию записи
  switch(dlg.m_ofn.nFilterIndex)  //В зависимости от выбранного формата
  {
  case 1: m_Rich.StreamOut(SF_TEXT,es); break;  //Записываем данные
  case 2: m_Rich.StreamOut(SF_RTF,es); break;    //в файл
  default: break;
  }
  }
}

Процедура записи данных в файл похожа на процедуру чтения. Мы пользуемся методом StreamOut(int nFormat, EDITSTREAM &es) класса CRichEditCtrl, который требует аргументами формат записываемых данных и структуру потока. Структура потока EDITSTREAM определяется заданием пункта назначения и функции записи. Добавим строку:

#include <algorithm>

в конец файла stdafx.h. Скомпилируем и запустим приложение. В результате, в соответствии с открытым текстовым документом, получается следующее: рис. 5.6 рис. 5.7 рис. 5.8

Рис. 5.6. Открытый текст в формате rtf

Рис. 5.7. Диалог шифрования

Рис. 5.8. Зашифрованный текст (ключ шифрования "крипто")

Приложение "Метод наименьших квадратов "

В данном параграфе, на примере создания приложения "Метод наименьших квадратов (МНК) ", рассматриваются следующие вопросы: диалог в качестве основного окна приложения, элемент управления CListCtrl, элемент управления CRichEditCtrl, класс CArray, работа с матрицами.

Постановка задачи. Теоретический материал

Пусть у нас есть следующая таблица:

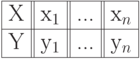
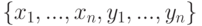
$\begin{tabular}{|r||r||r||r|} \hline X & x_1 & ... & x_n\\ \hline Y & y_1 & ... & y_n\\ \hline \end{tabular}$ $\{x_1,...,x_n,y_1,...,y_n\}$

Требуется построить полином y=f(x) заданной степени k: k меньше n-1 такой, что сумма квадратов расстояний от точек таблицы до графика полинома была наименьшей. Для поиска коэффициентов полинома составим следующий функционал:

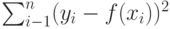
$\sum_{i-1}^n(y_i-f(x_i))^2$

и поставим задачу минимизации этого функционала F -> min. Полином запишем в виде

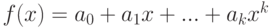
$f(x)=a_0+a_1{x}+...+a_k{x^k}$

тогда необходимое условие минимума запишется в виде:

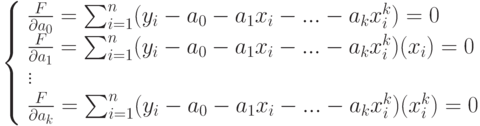
$\left\{ \begin{array}{l} \frac{\parial F}{\partial a_0}=\sum_{i=1}^n(y_i-a_0-a_1{x_i}-...-a_k{x_i^k})=0\\ \frac{\parial F}{\partial a_1}=\sum_{i=1}^n(y_i-a_0-a_1{x_i}-...-a_k{x_i^k})(x_i)=0\\ \vdots\\ \frac{\parial F}{\partial a_k}=\sum_{i=1}^n(y_i-a_0-a_1{x_i}-...-a_k{x_i^k})(x_i^k)=0 \end{array}$

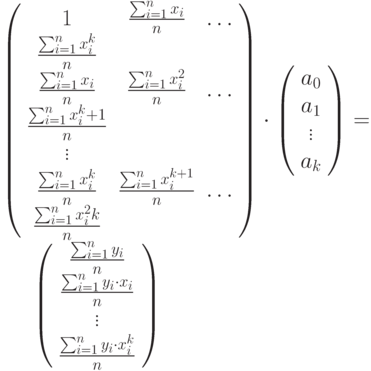
$\left( \begin{array}{ccc} 1 & \frac{\sum_{i=1}^n{x_i}}{n} &\ldots & \frac{\sum_{i=1}^n{x_i^k}}{n}\\ \frac{\sum_{i=1}^n{x_i}}{n} & \frac{\sum_{i=1}^n{x_i^2}}{n} &\ldots & \frac{\sum_{i=1}^n{x_i^k+1}}{n}\\ \vdots\\ \frac{\sum_{i=1}^n{x_i^k}}{n} & \frac{\sum_{i=1}^n{x_i^{k+1}}}{n} &\ldots & \frac{\sum_{i=1}^n{x_i^2k}}{n} \end{array} \right) \cdot \left( \begin{array}{c} a_0\\ a_1\\ \vdots\\ a_k \end{array}\right)= \left( \begin{array}{c} \frac{\sum_{i=1}^n{y_i}}{n}\\ \frac{\sum_{i=1}^n{y_i\cdot x_i}}{n}\\ \vdots\\ \frac{\sum_{i=1}^n{y_i \cdot x_i^k}}{n} \end{array}\right)$

Данная система имеет единственное решение, если k<n-1. Значит, существует единственный полином доставляющий минимум этому функционалу, с коэффициентами представимыми решением указанной системы. Напишем программу для нахождения коэффициентов полинома.

Дальше >>

Авторизоваться

Программирование под Windows в среде Visual C++ 2005

Разработка полноценных Windows-приложений

Приложение "Метод наименьших квадратов "

Постановка задачи. Теоретический материал

Вопросы и ответы