Обработка исключений

Практикум

Постройте таблицу значений функции 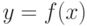для с шагом . Если в некоторой точке функция не определена, то выведите на экран сообщение об этом.

Замечание. При решении данной задачи использовать вспомогательный метод , реализующий заданную функцию, а также проводить обработку возможных исключений.

1. 

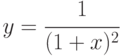
   Пример:

   using System;
   namespace Hello
   {
    class Program
    {
     static double f(double x)
     {
      try
      {
       //если х не попадает в область определения, то генерируется исключение 
       if (x == -1) throw new Exception();  
       else return 1 / Math.Pow(1 + x, 2);
      }
      catch
      {
       throw;
      }
     }
     
     static void Main(string[] args)
     {
      try
      {
       Console.Write("a=");
       double a = double.Parse(Console.ReadLine());
       Console.Write("b=");
       double b = double.Parse(Console.ReadLine());
       Console.Write("h=");
       double h = double.Parse(Console.ReadLine());
       for (double i = a; i <= b; i += h)
       try
       {
        Console.WriteLine("y({0})={1:f4}", i, f(i));
       }
       catch
       {
        Console.WriteLine("y({0})=error", i);
       }    
      }
      catch (FormatException)
      {
       Console.WriteLine("Неверный формат ввода данных");
      }
      catch
      {
       Console.WriteLine("Неизвестная ошибка");
      }
     }
    }
   }

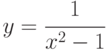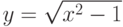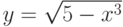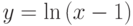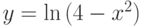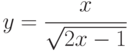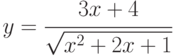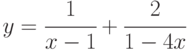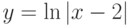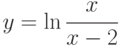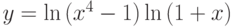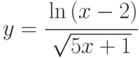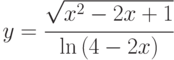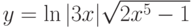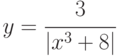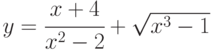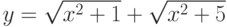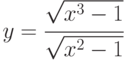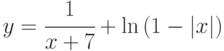2. ;	3. ;
4. ;	5. ;	6. ;
7. ;	8. ;	9. ;
10. ;	11. ;	12. ;
13. ;	14. ;	15. ;
16. ;	17. ;	18. ;
19. ;	20. ;