Опубликован: 19.02.2009 | Доступ: свободный | Студентов: 3107 / 832 | Оценка: 4.35 / 4.11 | Длительность: 16:28:00
ISBN: 978-5-94774-401-9
Специальности: Программист, Системный архитектор, Архитектор программного обеспечения
Лекция 6:
Рекурсивные методы
Практикум
-
Разработать рекурсивный метод (возвращающий значение):
- для вычисления
 -го члена следующей последовательности
-го члена следующей последовательности 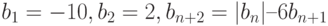 .
. - для вычисления
 -го члена следующей последовательности
-го члена следующей последовательности 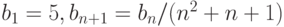
- для нахождения наибольшего общего делителя методом Евклида:
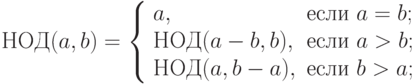
- для вычисления значения функции Аккермана для неотрицательных чисел
 и
и  . Функция Аккермана определяется следующим образом:
. Функция Аккермана определяется следующим образом: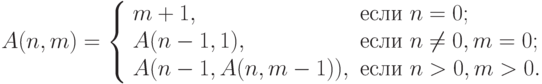
- для вычисления числа сочетаний
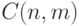 где
где 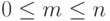 , используя следующие свойства
, используя следующие свойства при
при 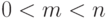 .
. - вычисляющий число а, для которого выполняется неравенство
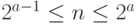 , где
, где 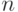 – натуральное число. Для подсчета числа а использовать формулу:
– натуральное число. Для подсчета числа а использовать формулу: 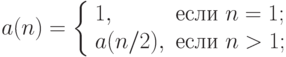
- для вычисления
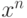 (
(  –вещественное,
–вещественное,  ,
а
,
а  –целое) по формуле:
–целое) по формуле: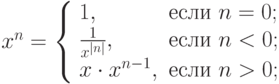 . Вычислить значение
. Вычислить значение 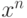 для различных
для различных  и
и  .
. - для вычисления
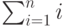 ,
где
,
где  – натуральное число.
Для заданных натуральных чисел
– натуральное число.
Для заданных натуральных чисел  и
и  вычислить с помощью разработанного метода значение выражения
вычислить с помощью разработанного метода значение выражения  .
. - для вычисления значения функции
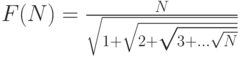 .
.Найти ее значение при заданном натуральном
 .
. - для вычисления цепной дроби:
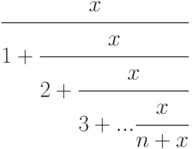 .
Найти значение данной дроби при заданном натуральном
.
Найти значение данной дроби при заданном натуральном  .
.
- для вычисления
-
Разработка рекурсивных методов ( не возвращающих значений):
- Даны первый член и разность арифметической прогрессии. Написать рекурсивный метод для нахождения
 -го члена и суммы
-го члена и суммы 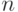 первых членов прогрессии.
первых членов прогрессии. - Даны первый член и знаменатель геометрической прогрессии. Написать рекурсивный метод для нахождения n-го члена и суммы
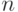 первых членов прогрессии.
первых членов прогрессии. - Разработать рекурсивный метод, который по заданному натуральному числу
 (
( 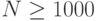 ) выведет на экран все натуральные числа не больше
) выведет на экран все натуральные числа не больше  в порядке возрастания. Например, для
в порядке возрастания. Например, для 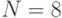 , на экран выводится
, на экран выводится 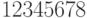 .
. - Разработать рекурсивный метод, который по заданному натуральному числу
 (
( 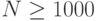 ) выведет на экран все натуральные числа не больше
) выведет на экран все натуральные числа не больше 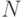 в порядке убывания. Например, для
в порядке убывания. Например, для 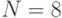 , на экран выводится
, на экран выводится  .
. - Разработать рекурсивный метод для вывода на экран стихотворения:
10 лунатиков жили на луне 10 лунатиков ворочались во сне Один из лунатиков упал с луны во сне 9 лунатиков осталось на луне 9 лунатиков жили на луне 9 лунатиков ворочались во сне Один из лунатиков упал с луны во сне 8 лунатиков осталось на луне ...... И больше лунатиков не стало на луне
- Дано натуральное число
 . Разработать рекурсивный метод для вывода на экран следующей последовательности чисел:
. Разработать рекурсивный метод для вывода на экран следующей последовательности чисел:
- Дано натуральное число
 . Разработать рекурсивный метод для вывода на экран следующей последовательности чисел:
. Разработать рекурсивный метод для вывода на экран следующей последовательности чисел:
- Разработать рекурсивный метод для вывода на экран цифр натурального числа в прямом порядке. Применить эту процедуру ко всем числам из интервала от
 до
до 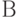 .
. - Разработать рекурсивный метод для перевода числа из десятичной системы счисления в двоичную.
- Разработать рекурсивный метод для перевода числа из двоичной системы счисления в десятичную.
- Разработать рекурсивный метод для вывода на экран всех делителей заданного натурального числа
 .
. - Дано натуральное четное число
 . Разработать рекурсивный метод для вывода на экран следующей картинки:
. Разработать рекурсивный метод для вывода на экран следующей картинки:
- Дано натуральное четное число
 . Разработать рекурсивный метод для вывода на экран следующей картинки:
. Разработать рекурсивный метод для вывода на экран следующей картинки:
- Дано натуральное число
 . Разработать рекурсивный метод для вывода на экран следующей картинки:
. Разработать рекурсивный метод для вывода на экран следующей картинки:
- Разработать рекурсивный метод для вывода на экран следующей картинки:
- Даны первый член и разность арифметической прогрессии. Написать рекурсивный метод для нахождения
Самостоятельная работа
Задача 1. Разработать рекурсивный метод для вывода на экран всех возможных разложений натурального числа n на множители (без повторений). Например, для n=12 на экран должно быть выведено:
2*2*3=12 2*6=12 3*4=12
Задача 2. Разработать рекурсивный метод для вывода на экран всех возможных разложений натурального числа n на слагаемые (без повторений). Например, для n=5 на экран должно быть выведено:
1+1+1+1+1=5 1+1+1+2=5 1+1+3=5 1+4=5 2+1+2=5 2+3=5
