НОУ ИНТУИТ | Концептуальное проектирование систем в AnyLogic и GPSS World. Лекция 11: Модель одбработки документов в организации

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.02.2013 | Доступ: свободный | Студентов: 257 / 0 | Длительность: 16:52:00

ISBN: 978-5-9556-0146-5

Темы: САПР, Программное обеспечение

Специальности: Архитектор программного обеспечения, Разработчик аппаратуры

Теги: AnyLogic, имитационные модели, модели, GPSS World

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Ключевые слова: группа, среднее время, поток, граф, отношение, вероятность, модельное время, программа

Постановка задачи

Для приёма и обработки документов в организации назначена группа в составе трёх сотрудников. Ожидаемая интенсивность потока документов - 15 документов в час. Среднее время обработки одного документа одним сотрудником - 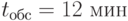$t_{обс}=12\text{ мин}$ . Каждый сотрудник может принимать документы из любой организации. Освободившийся сотрудник обрабатывает последний из поступивших документов. Поступающие документы должны обрабатываться с вероятностью не менее 95 %.

Определить, достаточно ли назначенной группы из трёх сотрудников для выполнения поставленной задачи.

Аналитическое решение задачи

Группа сотрудников работает как СМО с отказами, без очереди, состоящая из трёх каналов. Поток документов с интенсивностью $\lambda=15\frac{1}{час}$ можно считать простейшим, так как он суммарный от нескольких организаций. Интенсивность обслуживания $\mu=\frac {1}{t_{обс}}=\frac {60}{12}=5\frac{1}{час}$ . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.

Граф состояний СМО - это схема "гибели и размножения". Для неё имеются готовые выражения для предельных вероятностей состояний:

$Р_1=\frac {\rho}{1!}P_0, Р_2=\frac {\rho^2}{2!}P_0, …, P_n= \frac {\rho^n}{n!}P_0, P_{n+1}=\frac {\rho^{n+1}}{nn!}P_0, …, P_{n+m}=\frac {\rho^{n+m}}{n^mn!}P_0$

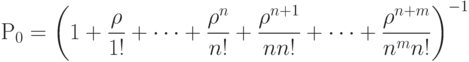
$Р_0=\left ( 1+\frac {\rho}{1!}+…+\frac {\rho^n}{n!}+\frac {\rho^{n+1}}{nn!}+…+ \frac {\rho^{n+m}}{n^mn!} \right )^{-1}$

Отношение $\rho = \frac {\lambda}{\mu}$ называют приведенной интенсивностью потока документов (заявок). Физический смысл её следующий: величина $\rho$ представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

В задаче $\rho = \frac {\lambda}{\mu}=\frac{15}{5}=3$

В рассматриваемой СМО отказ наступает при занятости всех трёх каналов, то есть $P_{отк}=P_3$ . Тогда:

$Р_0=\left ( 1+\frac {3}{1}+\frac {3^2}{2!}+\frac {3^3}{3!} \right )^{-1}=0,077, Р_3=\frac {3^3}{3!}P_0=4,5 \cdot 0,077=0,346$

Так как вероятность отказа в обработке документов составляет более 34 % (0,346), то необходимо увеличить количество сотрудников группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем $P_{отк}$ :

$Р_0=\left ( 1+\frac {3}{1}+\frac {3^2}{2!}+\frac {3^3}{3!}+\frac {3^4}{4!}+\frac {3^5}{5!}+\frac {3^6}{6!} \right )^{-1}=0,051$

$Р_6=\frac {3^6}{6!} P_0=\frac {729}{720} \cdot \frac {1}{19,412}=1,012 \cdot 0.051=0.052$

Теперь $Р_{обс}=1-Р{отк}=1-0,052\approx 0,95$

Таким образом, только группа из шести сотрудников сможет обрабатывать поступающие документы с вероятностью 95 %.

Решение задачи в AnyLogic

Создайте модель ОбрДокументов.

Выполните команду Файл/Создать/Модель на панели инструментов. Откроется диалоговое окно Новая модель.
В поле Имя модели диалогового окна Новая модель введите ОбрДокументов. Выберите каталог, в котором будут сохранены файлы модели.
Щелкните Далее. На второй странице Мастера создания модели выберите Начать создание модели "с нуля". Щелкните Далее.
Объекты и элементы модели ОбрДокументов показаны на рис. 10.1. Перетащите их на диаграмму класса Main, разместите, соедините и установите значения свойств согласно табл. 10.1.

Для ввода исходных данных используйте элементы Параметр, тип первых двух double, а третьего - int:

срИнтПост - средний интервал поступления документов, по умолчанию - 4;

Рис. 10.1. Объекты и элементы модели ОбрДокументов
срВрОбр - среднее время обработки документа, по умолчанию - 12;
колСотр - количество сотрудников, по умолчанию - 3.

Таблица 10.1.
Свойство	Значения
Имя	source
Класс заявки	Entity
Заявки прибывают согласно	Времени между прибытиями
Время между прибытиями	exponential(1/срИнтПост)
Количество заявок, прибывающих за один раз	1
Действие при выходе	постДокум++;
Имя	selectOutput
Выход true выбирается	При выполнении условия
Условие	delay.size()<колСотр
Имя	delay
Задержка задается	Явно
Время задержки	exponential(1/срВрОбр)
Вместимость	колСотр
Включить сбор статистики	Установить флажок
Имя	sink
Действие при входе	обрДокум++;
	верОбр=обрДокум/постДокум;
	верОтказа=1-верОбр;

Для вывода результатов моделирования используются элементы Простая переменная, тип которых double:

постДокум - количество поступивших документов;
обрДокум - количество обработанных документов;
верОбр - вероятность обработки документов;
верОтказа - вероятность не обработки документов.

AnyLogic-модель построена. Выделите в окне Проекты Simulation:Main. На странице Основные установите Фиксированное начальное число (воспроизводимые прогоны) и Начальное число: 1055. Перейдите на страницу Модельное время, выберите из списка Остановить: В заданное время. Введите Конечное время: 600000.0 (модельное время увеличено в 10 000).

Запустите модель. Вы должны получить результаты, приведенные на рис. 10.2.

Рис. 10.2. Результаты решения задачи в AnyLogic

Вероятность не обработки документов верОтказа=0,345, то есть отличается от полученного аналитическим путём решения на 0,001. Хотя это отличие можно отнести на счёт округления до трёх знаков после запятой.

Теперь измените количество сотрудников с трёх на шесть. Для этого выделите элемент Параметр с именем колСотр и установите по умолчанию 6. Всё остальные данные оставьте без изменения. Запустите модель. Вероятность не обработки документов верОтказа=0,051, то есть также отличается от полученного аналитическим путём решения на 0,001.

Сравнительную оценку можно было бы провести и при проведении расчётов с большим числом знаков после запятой, то есть с большей точностью.

Решение задачи в GPSS World

Программа с комментариями GPSS-модели обработки документов приведена ниже.

; Модель обработки документов в организации
T1  EQU  4  ; Среднее время поступления документов
T2  EQU  12  ; Среднее время обработки одного документа
Sotr  STORAGE    3  ; Количество сотрудников
VrMod  EQU    60  ; Время моделирования
; Сегмент имитации обработки документов
  GENERATE  (Exponential(1053,0,T1)); Источники документов
Met1  GATE SNF  Sotr,Met2  ; Не заняты ли сотрудники?
  ENTER  Sotr        ; Нет, тогда занять
  ADVANCE  (Exponential(1053,0,T2))  ; обработка
  LEAVE  Sotr        ; Освободить сотрудника
Met3  TERMINATE    ; Учёт обработанных документов  
Met2  TERMINATE    ; Учёт необработанных документов  
; Сегмент задания времени моделирования и расчёта результатов
  GENERATE   VrMod  
  TEST E  TG1,1,Met4  ; Если TG1=1, то расчет
; Вероятностей 
  SAVEVALUE  VerObr,(N$Met3/N$Met1); обработки
  SAVEVALUE  VerOtk,(1-X$VerObr)  ; необработки
Met4  TERMINATE  1
  START  10000  ; задание количества прогонов

При трёх сотрудниках в группе обработки документов вероятность необработки (VEROTK) такая же, как и при аналитическом решении задачи, что видно из фрагмента отчёта:

STORAGE CAP.REM.MIN.MAX. ENTRIES AVL. AVE.C. UTIL.
 SOTR    3   2   0   3    98161   1   1.963  0.654
SAVEVALUE                 RETRY       VALUE
 VEROBR                    0          0.654
 VEROTK                    0          0.346

При шести сотрудниках результаты моделирования также совпадают с результатами аналитического решения задачи.

Таким образом, в обеих системах имитационного моделирования получены одинаковые результаты, которые совпадают с достаточно высокой точностью с результатами аналитического решения задачи.

Замечание. Данная задача приводится автором на занятиях обучаемым и как поучительный пример для принятия решений на практике по причине, которая заключается в следующем.

Вполне логичным представляется первичное назначение группы сотрудников для обработки документов. Действительно, за один час в организацию поступают 15 документов. И три сотрудника также могут обработать за один час 15 документов. Каждый сотрудник по 5 документов.

Но элемент случайного их поступления, а также принятые условия, что обрабатывается свободным сотрудником последний поступивший документ, и вероятность обработки должна быть не менее 95 %, вносят свои коррективы, в которых мы убедились, решая эту задачу и аналитически, и в двух системах моделирования.

Дальше >>

Авторизоваться

Концептуальное проектирование систем в AnyLogic и GPSS World

Модель одбработки документов в организации

Постановка задачи

Аналитическое решение задачи

Решение задачи в AnyLogic

Решение задачи в GPSS World

Вопросы и ответы