Язык SQL
8.12 Многомерные данные в SQL
Выясним, что такое многомерные данные, где они используются и почему так важны. Может показаться странным, но многомерными данными всегда оперируют бухгалтеры и экономисты, даже если они сами не знают об этом. Когда говорят, скажем, о прибыли в разрезе филиалов и видов деятельности, имеются в виду именно данные, представляемые многомерными параллелепипедами. В нашем примере имеется один показатель "прибыль" и, по крайней мере, две координатных оси "название филиала" и "вид деятельности". Не оговорена, но заведомо предполагается третья ось. Назовём её "период времени". В соответствии с традицией используем термин "показатель" (measure), координатные оси будем называть измерениями (dimension), а конкретный набор значений измерений — фактом.
В экономическом анализе не существует теорий подобных физическим. Деятельность или состояние экономической системы, например, предприятия, оценивают, изучая некоторый набор показателей, зависящих обычно от нескольких параметров. Вот эти зависимости и дают информацию необходимую для управления системой.
Показатели представляют собой функции многих переменных (измерений). Их можно представлять многомерными (n=1, 2, 3, ...) параллелепипедами, которые, видимо для благозвучия, принято называть гиперкубами.
Понятно, что координатные оси могут существенно отличаться от физических величин. Могут использоваться и количественные характеристики, измеренные в различных шкалах, и качественные характеристики (теоретическая модель — решётка), и просто наименования (в теории — измерения в шкале порядка).
Введя в язык SQL средства для работы с многомерными данными, мы позволяем решать в нём задачи анализа деятельности систем. В важности этого класса задач сомневаться не приходится.
8.12.1 Откуда в табличной модели многомерные данные и как с ними работать
Откуда возьмутся многомерные таблицы в модели данных SQL, использующей реляционные таблицы? Они там были всегда. Просто мы не пытались их замечать, а изученная нами часть языка SQL не имела средств для работы с гиперкубами, и потому не давала поводов для поиска многомерного мира.
Более точно, любая реляционная таблица с ключом и с дискретными доменами столбцов может считаться представлением гиперкуба. Ключевые столбцы представляют измерения, не ключевые — показатели. В примере, приведенном в таблицах 8.9 и 8.10, реляционная таблица с двумя ключевыми столбцами "Год" и "Товар" образует двумерный гиперкуб, а столбец "Продано" — показатель.
| Год | Товар | Продано |
|---|---|---|
| 2010 | Т1 | 15 |
| 2010 | Т2 | 35 |
| 2011 | Т1 | 10 |
| 2011 | Т2 | 17 |
| 2012 | Т1 | 8 |
| 2012 | Т2 |
Если гиперкуб предназначен для непосредственного восприятия человеком, то ключевые домены должны содержать обозримое количество значений, хотя при анализе временных рядов последовательность значений может быть довольно длинной.
И ещё одно ограничение на семантику данных. В моделях реляционного типа первичную информацию не рассматривают как многомерную. Ценность представляют обобщённые данные, те самые показатели, имеющие смысл в предметной области.
Проблемы адресации
При переходе к многомерному представлению меняется способ адресации данных. Понятно, что для выбора одной ячейки гиперкуба 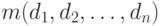 достаточно задать соответствующий факт, то есть набор значений всех измерений
достаточно задать соответствующий факт, то есть набор значений всех измерений 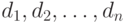 .Тут вроде бы ничего нового — чтение по заданному значению ключа. Допуская произвольные значения для
.Тут вроде бы ничего нового — чтение по заданному значению ключа. Допуская произвольные значения для  координат (
координат (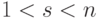 ), задаем гиперкуб размерности
), задаем гиперкуб размерности  , называемый обычно срезом. Ограничивая значения некоторых координат, получаем подкуб с тем же числом измерений.
, называемый обычно срезом. Ограничивая значения некоторых координат, получаем подкуб с тем же числом измерений.
Для задания областей сложной формы, в том числе многосвязных, необходимо определять принадлежность фактов размерности  или меньшей к некоторому списку. Нетрудно догадаться, что иногда такой список может быть не известен заранее и его придётся формировать специальным подзапросом.
или меньшей к некоторому списку. Нетрудно догадаться, что иногда такой список может быть не известен заранее и его придётся формировать специальным подзапросом.
Если необходимо не только читать, но с помощью присваиваний изменять значения некоторых фактов, то следует ввести оператор чтения значения показателя для текущего факта и фактов, вычисленных по текущему.
Теперь можно перейти к реализации многомерной модели на примере СУБД Oracle 10-й или 11-й версий. Можете, зайдя на сайт книги, установить Oracle XE и пользуясь имеющимися на сайте материалами выполнить все последующие примеры. Но лучше отложить конкретную работу до изучения раздела 10.3 "Объектно-реляционная модель данных Oracle".
Сейчас нам важно понять, как был изменён синтаксис SQL для работы с многомерными данными. На не менее важный вопрос: "На какой модели данных построен SQL?" мы ответим в конце главы.
8.12.2 Конструкция MODEL
Конструкция MODEL приписывается к запросу, подготавливающему исходные данные для многомерной модели. В сильно упрощённом виде синтаксис выглядит так:
<инструкция SELECT> MODEL DIMENSION BY (<список_столбцов >) MEASURES (<список_столбцов >) [RULES (список_правил)]
Фраза DIMENSION BY определяет размерности (то есть координатные оси) гиперкуба, одну или более. Фраза MEASURES задаёт измеряемые величины. Их может быть от одной и более. В секции RULES помещается множество правил, может быть пустое.
Простейший пример одномерного куба над таблицей emp выглядит так:
SELECT empno, ename FROM emp t MODEL DIMESION BY (empno) MEASURES (ename) RULES () ORDER BY empno;
В нём:
- empno используется как единственная размерность (DIMENSION);
- ename это единственная функция (MEASURE);
- действия над данными (RULES) не предусмотрены.
Результат работы, как и следовало ожидать, тривиальный (таблица 8.11).
| EMPNO | ENAME |
|---|---|
| 7369 | SMITH |
| 7499 | ALLEN |
| 7521 | WARD |
| 7566 | JONES |
| 7654 | MARTIN |
| 7698 |
В секции MEASURES можно записывать константы и выражения. Пример:
SELECT empno, ename, sal, date_now FROM emp MODEL DIMENSION BY (empno) MEASURES (ename, sal * 100 as sal, sysdate as date_now) RULES () ORDER BY empno;
8.12.3 Правила и адресация многомерных данных
Правила из секции RULES позволяют изменять любые значения показателей. Каждое правило состоит из левой части, определяющей ячейку или группу ячеек и соединённой с ней знаком присваивания (=) правой части. В правой части могут использоваться выражения, содержащие ячейки массива, литералы, функции языка SQL. Ячейки адресуются позиционно или символьно. Например, для функции sales, зависящей от prod и year, позиционная адресация sales['Book', 2011], а символьная sales[prod='Book', year=2011]. От способа адресации зависит обработка NULL^. Позиционная адресация позволяет обратиться к ячейке с NULL, а символическая нет.
Если в правилах указаны значения размерностей массива, которых нет в источнике данных, в результат будут добавлены записи с такими значениями размерностей. Так в исходной многомерной таблице создаются новые строки и столбцы.
Функция cv() в правой части присваивания дает доступ к текущему значению координаты (dimension).
Пример (создание показателя, которого нет в исходных данных):
SELECT * FROM emp MODEL DIMENSION BY (empno) MEASURES (job,ename, 0 sub_empno) RULES (sub_empno[any] = cv(empno) * 10 ) ORDER BY empno;
Результат запроса в таблице 8.12.
| EMP 110 | JOB | ENAME | SUB_EMPHO |
|---|---|---|---|
| 7369 | CLERK | SMITH | 73690 |
| 7499 | SALESMAN | ALLEN | 74990 |
| 7521 | SALESMAN | WARD | 75210 |
| 7566 | MANAGER | JONES | 75660 |
| 7654 | SALESMAN | MARTIN |
Пример более сложных правил в одномерном гиперкубе:
SELECT empno, job, ename FROM emp MODEL DIMENSION BY (empno) MEASURES (job, ename) RULES( job[7839] ='Boss', job[empno <> 7 839] = 'Employee', ename[empno BETWEEN 7369 and 7 4 99 ] = INITCAP(ename[CV(empno)])) order by empno;
Обратите внимание, ename[7839] указывает адрес ячейки в одномерном массиве. В остальных правилах задаются диапазоны. Структура правил в последнем примере:
- ename[7839] называется "cell reference" и определяет значение ename, для которого ключ из dimension by, то есть empno равен 7839. Для присваивания используется название "cell assignment)).
- Часть условия заключенная в квадратные скобки [7839], или [empno < 7788] называется "dimension reference) и может содержать как константы, так и различные условия. Для присваивания (cell asignment) можно использовать ключевое слово ANY — любое значение.
Условные выражения определяют множество значений, например, ename[empno < 7788] или ename[hiredate between 1999 and 2000].
Задание списка возможных значений может использовать следующие конструкции:
- FOR координата IN (список_значений);
- FOR координата IN (подзапрос);
- FOR координата FROM значение1 TO значение2 [INCREMENT | DECREMENT] значениеЗ.
В последнем случае при каждом повторе цикла "значение1" увеличивается либо уменьшается на "значение3", до тех пор пока не достигнет "значение2".
Существует многоколоночный цикл, который позволяет создать правила для групп в чём-то похожих столбцов.
В опции MODEL существует масса других возможностей, в частности, средства для итерационной обработки. Мы их не рассматриваем. Наша задача — понять идею построения многомерной модели в SQL.
В самом общем изложении — строится запрос, выбирающий базисные данные, на них определяется структура эмулируемой многомерной области, а правила задают выполняемые преобразования.
В качестве полезного размышления попробуйте представить синтаксис расширения SQL для какой-нибудь известной вам предметной области, например, семантических сетей или сетей Петри.
