Реляционная модель данных
4.8 Независимые операции реляционной алгебры
Для выделения независимых операций реляционной алгебры выделим базисный набор свойств операций, так чтобы все особенности операций отражались наиболее полно. Перечислим базисные свойства понятия "реляционная операция":
- увеличение количества атрибутов отношений;
- уменьшение количества атрибутов отношений;
- сохранение количества атрибутов отношений;
- сравнение атрибутов;
- работа с данными однотипных отношений;
- изменение имён.
Заметим, что независимость свойств и полнота этой системы свойств не доказаны.
Утверждение. Объединение, вычитание, декартово произведение, выборка и проекция независимые (примитивные) операции. Их нельзя выразить друг через друга.
Покажем это.
В самом деле, увеличивают число атрибутов декартово произведение и соединения.
Уменьшает число атрибутов только проекция. Поэтому она не выразима через остальные операции, не обладающие этим свойством.
Сравнивают атрибуты только селекция, выбирающая строки, и частное, основанное на выделении группы строк.
С данными нескольких однотипных отношений могут работать только булевы операции. Поэтому выделяем их в отдельную группу. Выбор группы строк основан на выборе строки по условию. Можно считать независимой более простую операцию селекции.
Изменение имён выполняет только операция переименования.
Разберёмся с булевыми операциями: объединением, пересечением и разностью. Кроме них сохраняют количество атрибутов отношения ещё селекция и пересечение. Но они не имеют теоретико-множественной природы. Так что выделение булевых операций обоснованно.
Используя известные свойства булевой алгебры, можно утверждать, что операции объединения и разности независимы.
В самом деле, пересечение определяется через вычитание 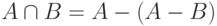 , а частное через вычитание, декартово произведение и проекцию:
, а частное через вычитание, декартово произведение и проекцию:

Итак, заведомо независимыми будут проекция, селекция, частное и переименование.
Разберёмся с тройкой — декартово произведение, естественное и соединения. Операции соединения определяются через операции декартового произведения и выборки.
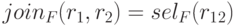
Так что естественно считать независимой, в некотором смысле более простую, операцию декартово произведение.
4.9 Определение реляционной алгебры
Обозначим:
 — множество атрибутов (универсум),
— множество атрибутов (универсум),
 — множество доменов,
— множество доменов,
 — полная функция
— полная функция  :
:  ; назначает домен каждому атрибуту,
; назначает домен каждому атрибуту,
 — множество всех возможных схем отношений на
— множество всех возможных схем отношений на  ,
, 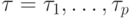 —есть множество отношений
—есть множество отношений 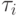 со схемами
со схемами 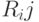 , соответственно,
, соответственно,
 —множество бинарных отношений, определенных на доменах из
—множество бинарных отношений, определенных на доменах из  , содержащее, по крайней мере, отношение равенства и неравенства для каждого домена.
, содержащее, по крайней мере, отношение равенства и неравенства для каждого домена.
Определение. Реляционной алгеброй над  ,
,  ,
, ,
,  , \tau,
, \tau,  называется семиместный кортеж
называется семиместный кортеж

где  — это множество, содержащее операции селекции, проекции, объединения, пересечения, разности, частного, естественного и
— это множество, содержащее операции селекции, проекции, объединения, пересечения, разности, частного, естественного и  -соединения, а также операцию переименования атрибутов из
-соединения, а также операцию переименования атрибутов из  .
.
Перечислим основные особенности реляционной алгебры:
- Алгебра строится на множестве отношений с атрибутами.
- Элементы данных (атрибуты) типизированы (относятся к одному домену).
- Отношения можно соединять. Связей между отношениями, подобных рассмотренным в "Модель сущность-связь" , не существует, так как по природе своей связи требуют активности системы и потому не являются алгебраической конструкцией.
- Используются операции над множествами (объединение, пересечение, вычитание, декартово произведение, частное) и реляционные операции (выборка (селекция), проекция, соединения, деление).
- Для выполнения некоторых операций необходимо обеспечить совместимость отношений по сигнатуре.
- В некоторых случаях операции требуют переименования атрибутов.
- Выражения реляционной алгебры строятся на отношениях и возвращают отношения же. Отношения-результаты можно использовать как аргументы в других выражениях.
- Независимость операций. Операции соединение, пересечение и деление можно выразить через другие реляционные операции. Операции объединение, вычитание, декартово произведение, выборка, проекция нельзя выразить друг через друга.
- Реляционная алгебра — это язык запросов. Выразить создание исходных отношений, заполнить их, изменить или удалить кортежи в этой алгебре нельзя.
4.10 Примеры запросов
Как вы помните, мы договорились, по всем разделам решать примеры, которые помогут в освоении материала. Для изучения запросов в реляционной алгебре будет использовано свободно доступное инструментальное средство WinRDBI, созданное в университете штата Аризона. В последующих главах мы будем использовать его для работы с запросами в исчислениях на кортежах и доменах. Можно поработать и в первой версии языка SQL, которая в существующих СУБД не используется.
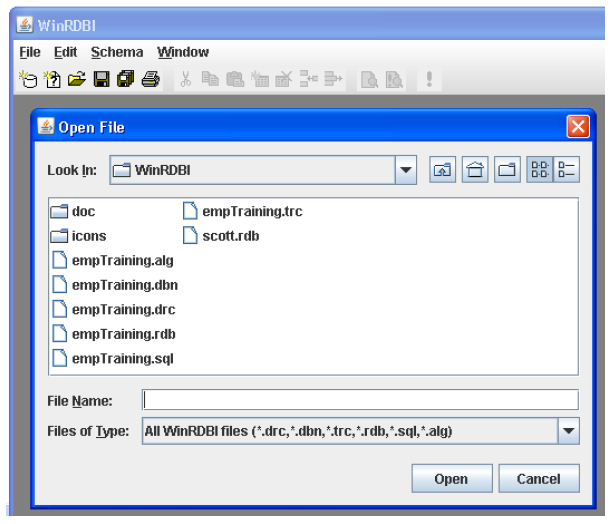
4.10.1 Устанавливаем WinRDBI
Скачиваем файл дистрибутива WinRDBISetup-3.1.0.130 с сайта http://winrdbi.asu.edu/ и, щёлкнув по нему левой кнопкой мыши, инсталлируем WinRDBI. Скачиваем с сайта книги дополнительную схему базы данных, находящуюся в текстовом файле scott.rdb. Помещаем этот файл либо непосредственно в область баз данных показанную на рисунке 4.9, либо в корневую папку WinRDBI, хранящую эти данные. На моей машине это папка C:\Program Files\WinRDBI. Чтобы загрузить схему scott.rdb, наберите File > Open и выберите путь к файлу scott.rdb. Файлы с расширением .rdb хранят базы данных. Изначально имеется файл empTraming.rdb, и мы только что добавили scott.rdb. Файл empTraining.alg хранит набор запросов в реляционной алгебре. В остальных файлах с именем erpTraining хранятся запросы в исчислениях и SQL.
4.10.2 Схема scott
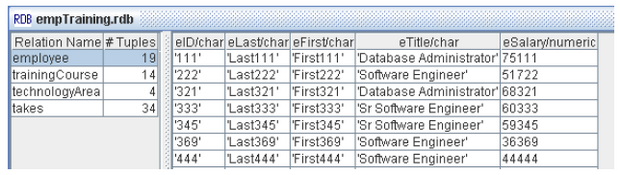
Рассмотрим отношение employee (рисунок 4.10), входящее в схему erpTraining. Атрибуты обозначены именами, начинающимися со строчной буквы, за которыми следует имя типа, отделённое знаком "/". Эти особенности связаны с тем, что WinRDBI написан на языке Пролог.
Формат текстового файла .rdb несложен. Вы можете разобраться в нём самостоятельно, прочитав файлы empTraining.rdb и scott.rdb с помощью текстового редактора. Строчные значения заключаются в одинарные кавычки.
В схеме scott (рисунок 4.11) заданы отношения emp, dept, salgrade, описанные на сайте книги.
Обратите внимание на то, что в отношении emp появились текстовые значения 'null'. Дело в том, что неопределённых значений в реляционной лгебре не существует. Поэтому NULL был заменён текстовой константой 'null', не эквивалентной ему по смыслу, а числовые значения атрибута comm пришлось заменить текстовыми, заключив их в кавычки.
4.10.3 Обозначения операций
Обозначения операций реляционной алгебры сведены в таблицу 4.1
| Операция реляционной алгебры | Операция в WinRDBI |
Проекция 
|
project X (r) |
Селекция 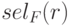
|
select F (r) |
Естественное соединение 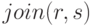 , или , или 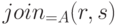 , или r join s , или r join s
|
r njoin s |
 -соединение -соединение |
не поддерживается |
Декартово произведение 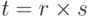
|
r product s |
Частное r division s , или  , или , или 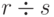
|
не поддерживается |
Объединение 
|
r union s |
Пересечение 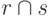
|
r intersect s |
Разность 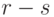
|
r difference s |
 -соединение и частное не поддерживаются. Их необходимо выражать через другие операции. Выполните следующую последовательность File > Open > empTraining.alg. В появившейся панели изучите образцы запросов реляционной алгебры. Обратите внимание на то, что результат запроса —это временное отношение, и на нём, в свою очередь, можно выполнять запросы. Если результат запроса поименован, то после выполнения запроса, образованное отношение-ответ сохраняется и доступно для дальнейшей работы.
-соединение и частное не поддерживаются. Их необходимо выражать через другие операции. Выполните следующую последовательность File > Open > empTraining.alg. В появившейся панели изучите образцы запросов реляционной алгебры. Обратите внимание на то, что результат запроса —это временное отношение, и на нём, в свою очередь, можно выполнять запросы. Если результат запроса поименован, то после выполнения запроса, образованное отношение-ответ сохраняется и доступно для дальнейшей работы.
4.10.4 Примеры запросов
Для создания запроса необходимо выполнить следующую последовательность действий (рисунок 4.13):
- Нажать кнопку
- Выбрать Relational Algebra.
- Нажать Ok.
В появившейся панели можно набирать текст запроса.
Примеры запросов
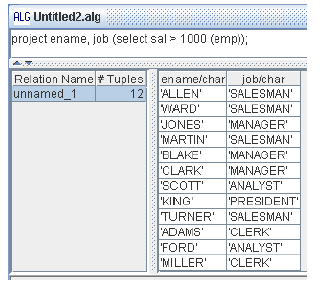
- Выдать фамилии и должности лиц, получающих зарплату больше 1000. Рисунок 4.14.
- Выдать список сотрудников в виде отношения с атрибутами: empno, ename, job, dname. Запрос: project empno, ename, job, dname (emp njoin dept);