Иерархические модели данных. Деревья в СУБД Cache
3.3 Деревья и разреженные массивы
Теперь, изучив ObjectScript, мы может заняться организацией иерархических баз данных в Cache. Поскольку запросы в них имеют навигационный характер, необходимо освоить команды, позволяющие определить свойства узлов, организовать поиск в ширину и глубину.
Дополнительно будет рассмотрена команда копирования индексированных переменных, которая упростит групповые вставки.
3.3.1 Разреженные массивы и их представление деревьями
Представим набор записей в виде массива, в котором имя массива — это имя набора, а имена индексов это имена полей записи. Значениями индексов в такой модели хранения данных будут значения полей. Если хотя бы один домен имеет мощность континуума, например, домен с вещественными числами, то ограничиться целочисленными индексами, как в массивах, изучаемых в математике, не удастся.
В языках общего назначения при определении массива с конечным набором значений индексов необходимо задать его размерность. Это необходимо, чтобы выделить область памяти, достаточную для хранения массива. Такие традиционные массивы будем называть плотными. В практически важных моделях данных такой массив сильно разрежен. Большую часть выделенного объёма занимают пустые места, соответствующие комбинациям значений индексов, которые не могут быть использованы или ещё не использованы.
Разреженные массивы, реализованные в Cache, отличаются следующими особенностями:
- Хранятся только имеющиеся данные, место под все возможные комбинации индексов не выделяется.
- Размерность массива теоретически не ограничена, а практически ограничивается только длиной строки, в которую помещается запись всех значений индексов.
Вторая ипостась разреженного многомерного массива — это дерево. Нетрудно догадаться, что если присутствуют не все узлы, необходимые для образования дерева, то, может быть, придётся вводить в рассмотрение так называемые виртуальные узлы.
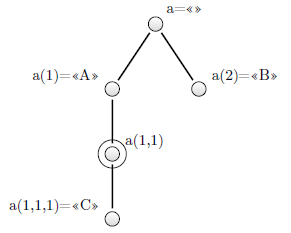
Рассмотрим пример. Создадим дерево в виде локала из следующих узлов: a(1)="A", a(2)="B", a(1,1,1)="C". В узле a(1)="A" единица —это индекс, "А" — значение узла a(1). Строго говоря, дерево получается (рисунок 3.22), только если считать, что к заданным узлам добавлен корневой узел a="" (его значение пустое, но могло быть любое другое) и промежуточный узел a(1,1). Последний называется виртуальным узлом. Такие узлы имеют имя и индексы, но не имеют значения. Их предназначение — связать узлы, отличающиеся на два и более индексов, чтобы на каждом следующем уровне дерева добавлялся ровно один индекс. Виртуальные узлы будем изображать двумя концентрическими окружностями.
Не думайте, что виртуальные узлы вводятся в угоду теории. В следующем разделе станет понятно, что без них невозможна навигация по деревьям.
Замечание. Вы, конечно, заметили, что мы следуем противоестественной привычке математиков высаживать деревья вверх корнями.
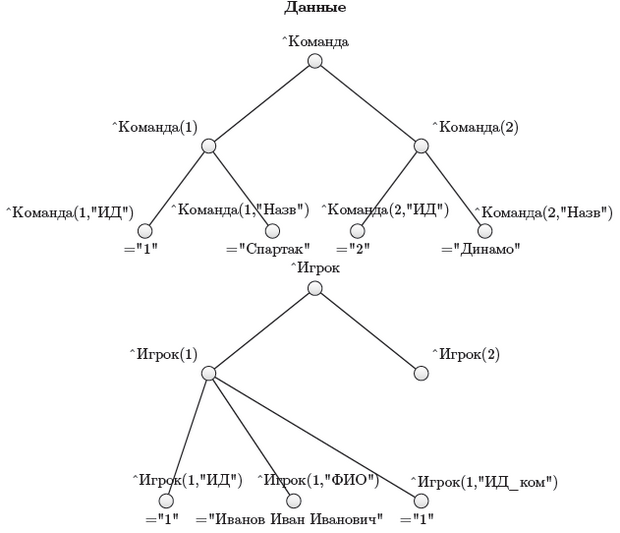
Набор деревьев (лес) всегда можно свести в одно дерево или небольшое их число. На рисунке 3.23 представлены в экземплярах две связанные сущности "Команда" и "Игрок", ранее рассматривавшиеся в разделе 2.2.7 (рисунок 2.19).
Сущность "Команда" с экземплярами представлена на рисунке 3.23 деревом глубины 2. Заметим, что можно было бы ограничиться деревом глубины 1. В этом случае в нем на уровне 1 существовали бы узлы вида ^Команда (1) =" 1 "Спартак" или ^Команда (1)=$lb(" 1","Спартак") или что-нибудь ещё.
Позже вы увидите, что именно так хранятся строки таблиц в реализации реляционной модели.
В варианте, представленном на рисунке 3.23рисунке 3.50, данные каждой сущности хранятся в своём дереве, а для всех метаданных использовано дополнительное дерево (рисунке 3.24). Поясним значения листовых узлов. РК—первичный ключ, NK —не ключ, FK—внешний ключ. Значения узла лМетадан-ные ( "Связь", "Связь1" ) представлено строкой с разделителем """
Можно объединить все деревья в одно, выполнив необходимые переименования (рисунок 3.25)
Кроме констант и простых переменных узел может принимать следующие значения:
-
строка с разделителями, например,
K ^a S ^a(1)="a%b%c" W ^a(1)
-
список, например,
K ^a S ^a(1,1,1)=$LB("a","b") W ^a(1,1,1),"~",$P(^a(1,1,1),2) -
значение узла другого массива, например,
K ^b S ^b(1)="b1", ^b(2)="b2", ^b(1,1)="b11" S ^a(1,1,1)=^b(1) W ^a(1,1,1)
В соответствии с известным выражением, вы вольны расширять глобал в любую сторону своей души. Это не означает, конечно, что все варианты будут работать одинаково эффективно.
В результате создана база, содержащая данные и метаданные, организованные в иерархии. Система управления базой отсутствует. Все манипуляции с данными и метаданными и запросы данных придётся выполнять врукопашную. Контроль ограничений целостности не организован. Связь обозначена, но необходимо дописать процедурную часть, обеспечивающую её работу.