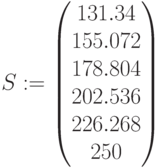Оптимизационные модели
4.5. Оптимизация межотраслевого баланса
Возможность оптимизации межотраслевого баланса появляется, если коэффициенты прямых затрат отражают затраты не средние по отрасли, а для каждого способа и технологии производства. В таких моделях межотраслевого баланса представлено отдельно производство каждого вида продукции. Построение оптимизационных моделей межотраслевого баланса позволяет в условиях ограниченности ресурсов находить наиболее эффективные комбинации ресурсов для максимизации конечного продукта [22].
Задача 4.7.
Крупное структурное предприятие состоит из 6 подразделений, каждый из которых выпускает по 1 виду продукции. Отношения между подразделениями определены технологической матрицей прямых затрат. В таблице 4.8 указаны нормы прямых затрат подразделений, используемых в качестве промежуточного продукта для выпуска единицы продукции для каждого подразделения. Известны максимально допустимые ресурсы подразделений предприятия. Известны цены на готовую продукцию, которая направляется на внешний рынок. Оптимизировать новую программу – плановую валовую продукцию, так, чтобы распределение готовой продукции на собственные потребности и экспорт, давало максимальный доход от реализованной продукции.
| Подразделение 1 | Подразделение 2 | Подразделение 3 | Подразделение 4 | Подразделение 5 | Подразделение 6 | Цена | |
| Подразделение 1 | 0,01 | 0,03 | 0,05 | 0,07 | 0,09 | 0,12 | 2 |
| Подразделение 2 | 0,03 | 0,05 | 0,06 | 0,08 | 0,1 | 0,13 | 6 |
| Подразделение 3 | 0,05 | 0,07 | 0,07 | 0,09 | 0,11 | 0,14 | 3 |
| Подразделение 4 | 0,07 | 0,09 | 0,08 | 0,1 | 0,12 | 0,15 | 7 |
| Подразделение 5 | 0,09 | 0,11 | 0,09 | 0,11 | 0,13 | 0,16 | 8 |
| Подразделение 6 | 0,11 | 0,13 | 0,1 | 0,12 | 0,14 | 0,17 | 1 |
| Ресурсы подразделений | 400 | 300 | 900 | 500 | 450 | 250 |
Модель задачи.
Входные переменные:
-
 –количество подразделений ,
–количество подразделений ,  – текущий номер подразделения - производителя,
– текущий номер подразделения - производителя,  – текущий номер подразделения-потребителя
– текущий номер подразделения-потребителя -
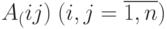 - матрица прямых затрат,
- матрица прямых затрат, -
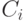 - цены на готовую продукцию, которая направляют на внешний рынок,
- цены на готовую продукцию, которая направляют на внешний рынок, -
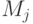 – допустимые мощности подразделений, ресурсы,
– допустимые мощности подразделений, ресурсы,
Управляемые переменные - 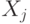 - вектор плановой валовой продукции.
- вектор плановой валовой продукции.
Выходные показатели –
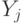 -. конечная продукция подразделений,
-. конечная продукция подразделений,
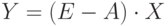 - в соответствии с уравнением межотраслевого баланса,
- в соответствии с уравнением межотраслевого баланса, 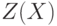 - доход от реализации конечной продукции на внешнем рынке..
- доход от реализации конечной продукции на внешнем рынке..
Целевая функция –оптимизируемый параметр – доход от реализации конечной продукции.
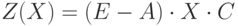
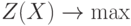
Ограничения.
 – ресурсные ограничения
– ресурсные ограничения
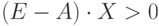 – конечный продут положителен,
– конечный продут положителен,

В результате имеем систему уравнений.
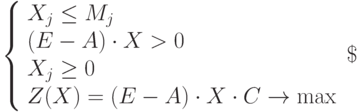 |
( 4.12) |
Решение. В программе Mathcad задача решается в матричном виде, аналогично всем приведенным примерам. Система уравнений с оптимизацией решается численно с помощью блока  и функции
и функции  .
.
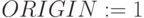
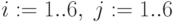
Матрица промежуточных потоков затрат: 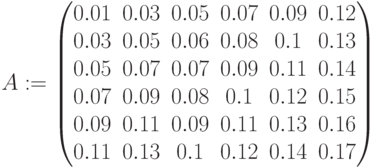
Ресурсы подразделений: 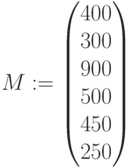
Цена: 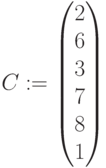
 – валовый планируемый выпуск
– валовый планируемый выпуск
 – доход от реализации конечной продукции – целевая функция
– доход от реализации конечной продукции – целевая функция
Решение:
Начальные значения:
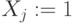 ,
, 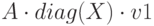 – затраты – сумма по столбцам
– затраты – сумма по столбцам

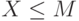
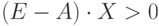

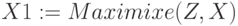
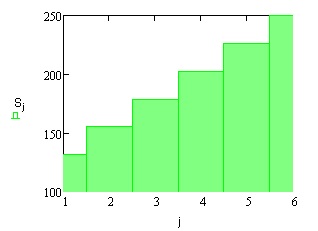
Оптимальный план валового выпуска: 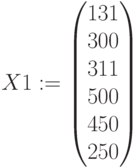
Конечная продукция:  ,
, 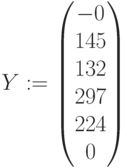
Оптимальный доход: 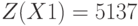
Промежуточные поставки: 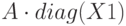 ,
, 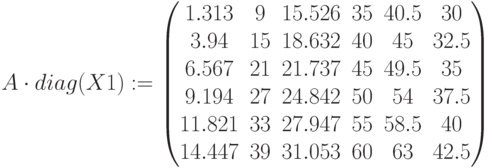
Основные итоги
Рассмотрены основные типы оптимизационных задач.
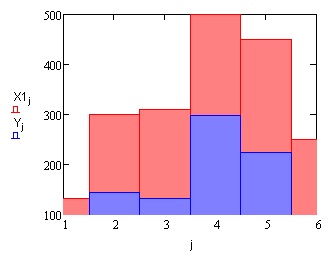
Задача формирования оптимальной производственной программы - три модели: модель получения максимальной прибыли без заданного плана и с планом, модель в комплектной постановке - получение максимальной доли плана выпуска продукции при нехватке ресурсов, т-модель - нахождения минимума дополнительного количества ресурсов, необходимых для выполнения полного плана. Две модели транспортной задачи. Задача оптимального комплектования штата работников. Задача максимизации конечного продукта в схеме межотраслевого баланса. Для каждой задачи определены входные данные, построена математическая модель. Каждая модель представлена в Mathcad в виде системы матричных уравнений. Системы уравнений решены численно - в блоке 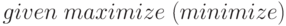 . Построены диаграммы результирующих данных.
. Построены диаграммы результирующих данных.
Ключевые термины
Оптимизационная задача – задача, цель которой состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия варианта использования имеющихся ресурсов.
Оптимизационная модель – математическая модель решения оптимизационной задачи.
Математическое программирование - направление математики, изучающее методы решения оптимизационных задач.
Целевая функция – функция, определяющая критерий оптимальности в оптимизационной задаче.
Управляемые переменные - переменные целевой функции, которые подвергаются изменению в процессе поиска решения.
Ограничения – системы уравнений и неравенств, ограничивающих область решения оптимизационной задачи в соответствии с заданными условиями.
Нормированная стоимость - изменение целевой функции при изменении соответствующего управляемого параметра на единицу.
Транспортная задача - оптимизационная задача оптимального прикрепления потребителей к поставщикам при доставке грузов.
Задача оптимального распределения трудовых ресурсов – оптимизационная задача распределения трудовых ресурсов при выбранном критерии оптимальности.

 – единичная
– единичная 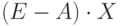 –
– 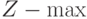
![Z(X):=[(E-A)\cdot X]\cdot C](/sites/default/files/tex_cache/978f1bae5ff81c668beaa094c31629d5.png) ,
, 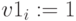 – единичный
– единичный  ,
,