Определение риска
Отношение к риску
По отношению к риску люди могут разделяться на склонные к риску, не склонные к риску и нейтральные к риску. Для проведения такой классификации необходимо провести количественное описание какого-то параметра , связанного с отношением к риску. В качестве такого параметра предложено использовать функцию полезности, которая ставит в соответствие каждому возможному состоянию Х субъективную полезность этого результата U(X). Субъективная полезность не может быть измерена , не имеет размерности и для каждого состояния Х может иметь различные значения для разных субъектов. Например, можно считать , что благосостояние в 1000 рублей для студента соответствует большему значению полезности, чем та же сумма для состоявшегося предпринимателя. Для разных людей функции полезности индивидуальны, но они могут быть похожими.
Для функции полезности определены определенные характеристики, которым она должна удовлетворять [ 3 ]. Основные из них: никакое резкое изменение благосостояния не может резко изменить функцию полезности; функция полезности не должна претерпевать изломы.
Принимая решение, предприниматель не знает точно, какой результат будет достигнут, какое состояние у него образуется в результате принятого решения (игра с природой). В общем случае этот результат может принимать Хi значений, каждое из которых характеризуется вероятностью Рi. Математическое ожидание результата такого действия будет:
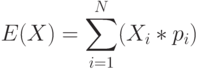
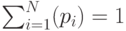
В результате принятия решения благосостояние предпринимателя изменится и его будущее благосостояние будет равно сумме первоначального благосостояния плюс результат принятого решения:

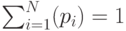
Каждому состоянию благосостояния W можно сопоставить субъективную полезность этого благосостояния U(W) и ввести понятие ожидаемой полезности принятого решения:
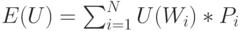 , где
, где 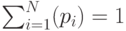
Для оценки полезности принятого решения вводится понятие справедливой игры или Объективной денежной оценки ОДО. Это понятие связывается со стоимостью принимаемого решения и в случае, если эта стоимость равна потенциальному выигрышу, игра считается справедливой.
Всех индивидуумов можно разделить на три группы, в зависимости от того, как они соотносят свое благосостояние после игры со своим начальным состоянием перед игрой.
Если индивидуум считает, что его благосостояние после игры (с учетом уплаты справедливой цены за игру) не изменится, то он нейтрален к риску. Это состояние можно описать уравнениями:
E(U(W = U(W0))) или E(U(X + W0 – E(X))) = U(W0).
Если для индивидуума ожидаемая полезность состояния после игры меньше полезности его благосостояния перед игрой, то он не склонен к риску. Это отношение определяется неравенством:
E(U(X + W0 – E(X))) < U(W0)
Если для индивидуума ожидаемая полезность состояния после игры больше полезности его благосостояния перед игрой, то он склонен к риску. Это отношение определяется неравенством:
E(U(X + W0 – E(X))) > U(W0)
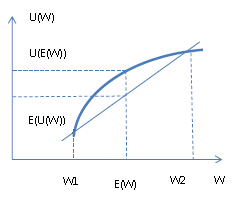
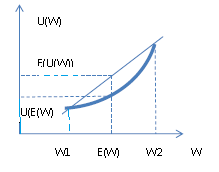
Графически отношение к риску может быть представлено в виде рисунков 1.1, 1.2. Если функция полезности линейна, то субъект нейтрален к риску, если функция полезности выпукла вверх, то субъект склонен к риску, если функция полезности выпукла вниз, то субъект не склонен к риску.
Разница между справедливой ценой игры и субъективной оценкой участника этой игры показывает, как конкретный индивидуум оценивает для себя риск, связанный с данной игрой. Эта разница получила название премия за риск:
Исследования Эрроу и Пратта показали, что премия за риск определяется:
- Возможным результатом игры и их вероятностями;
- Видом функции полезности игрока;
- Начальным благосостоянием игрока.
Для вывода этого заключения было рассмотрено уравнение:
E(U(W0 + X)) = U(W0 + E(X) - ?)1.1.
При малом отклонении результатов игры от начального значения справедливо разложить правую часть этого уравнения в ряд Тейлора до линейного члена в окрестности точки (W0+E(X)):
U(W0 + E(X) – ?) = U(W0 + E(X)) + U' (W0 + E(X)) * (-* U'' (W0 + E(X)) * (X-E(X))2,)
Разложение U(W0 + X) в ряд Тейлора дает:
U(W0 + X) = U(W0 + E(X))+U'(W0 + E(X)) * (X-E(X)) + ? * U'' (W0 + E(X)) * (X-E(X))2,
Учитывая, что E(X-E(X))=0, и E((X – E(X))2) = D(X), получим:
U(W0 + X) = U(W0 + E(X))+ ? * U'' (W0 + E(X)) * D(X),1.2.
При E(X)=0, сравнивая уравнения (1.1) и (1.2), получим:
? = ? *D(X) * U''(W0)/U'(W0)
, где U'(W0) = dU(W) / dW и U''(W0) = d2 U(W) / dW2 - первая и вторая производные от функции полезности, вычисленные в точке начального благосостояния W0. D(X) – некоторая функция, зависящая от набора возможных результатов игры. Зависимость выведена для условия, что в результате игры начальное благосостояние изменяется незначительно.
Таким образом, рисковая премия состоит из двух составляющих:
D(X) - которая определяется только игрой и не зависит от свойств индивидуума, который принимает решения;
A(W0) = U''(W0)/U'(W0) – характеристика отношения индивидуума к риску и зависит от его функции полезности, эта составляющая получила название коэффициента абсолютной несклонности к риску, или абсолютного коэффициента Эрроу-Пратта, а величина
R(W0) = A(W0) *W0
получила название коэффициента относительной несклонности к риску или относительного коэффициента Эрроу-Пратта.
Премия за риск может быть положительной, при этом субъективная ценность игры меньше E(W), может быть отрицательной, при этом субъективная ценность игры больше E(W).
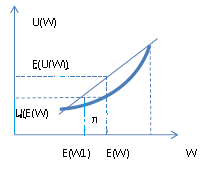
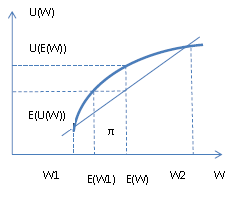
Субъективную цену можно вычислить, если знать функцию полезности индивидуума, условия игры и начальное благосостояние. Для этого необходимо ожидаемую полезность игры уравнять с полезностью некоторой суммы денег E(W1). Эта сумма денег показывает, какое состояние по интуитивному ощущению индивидуума будет у него после игры. На рис. 1.3 , 1.4. показаны премии за риск для не склонного и склонного к риску субъектов.