Лекция 10: Арифметические операции над числами с плавающей запятой
Деление чисел с плавающей запятой
Сначала рассмотрим случай деления двух чисел с плавающей запятой в десятичной системе счисления.
(0,6*105) * (0,2*102) = 3 * 105-2 = 0,3 * 104
Последний шаг выполнен для нормализации мантиссы результата.
Таким образом, если представить операнды в двоичной системе счисления как
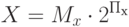
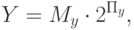
а частное мы хотим тоже получить в виде числа с плавающей запятой, то есть
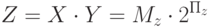
то деление сводится к двум простейшим действиям, рассмотренным ранее: вычитанию порядка делителя из порядка делимого как целых чисел и делению мантисс как операндов с фиксированной запятой. При необходимости к ним добавляется еще нормализация мантиссы результата:
Пz = Пx - Пy
Mz = Mx / My
На первом этапе (вычитание порядков) мы имеем дело с числами с фиксированной точкой. В результате их вычитания возможны как положительное, так и отрицательное переполнения.
Предполагая, что мантиссы обоих операндов нормализованы, то есть удовлетворяют условию
1 > |Mx,y| ? 2-1,
мы получим
2 > |Mz| = |Mx| / |My| ? 2 -1
Таким образом, если в результате деления мантисс и потребуется нормализация (в случая, если 2 > |Mz| ? 2-1), то она может быть выполнена сдвигом вправо не более чем на один разряд. При этом к порядку должна быть добавлена единица. Обычно такая ситуация проверяется на первом шаге деления мантисс. Для чисел с фиксированной запятой ситуация, когда |Mx| ? |My| приводит к приостановке деления и выработке сигнала особого случая, который обрабатывается системным программным обеспечением ЭВМ. В случае чисел с плавающей запятой такая ситуация ведёт к коррекции мантиссы делимого (Mx' = Mx / 2) и соответствующему изменению порядка (Пx' = Пx + 1) с последующим делением мантиссы Mx' на Y.
Рассмотрим особые случаи при делении чисел с плавающей запятой
- Пz = Пx - Пy
- Если Пz = +?, то Z = ?
- Если Пz = -?, то продолжить деление, так как в последующем возможно увеличение порядка за счет того, что мантисса X окажется больше или равной мантиссе Y.
- Mz = Mx / My
Т.к. |Mx| ? 2-1, |My| ? 2-1, то 2 > |Mz| ? 2-1
Возможная область ненормализованной мантиссы:
2 > |Mz| ? 1
Если |Mz| ? 1, то выполнить нормализацию мантиссы с одновременной коррекцией порядка:
|Mz| = |Mz| * 2-1; Пz = Пz + 1.
Если в результате получим Пz = +?, то Z = ?.
Если в ходе деления мантисс получили Пz = -?, и Пz = Пz +1 = -?, то Z = 0.
Если в ходе деления мантисс получили |Mz| < 1, и при обработке порядков получили Пz = -?, то Z = 0.
Сложение/вычитание чисел с плавающей запятой
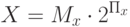
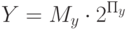
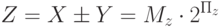
Рассмотрим несколько примеров сложения/вычитания чисел с плавающей запятой в десятичной системе счисления.
Пример 1.
(0,3*103) + (0,98*104) = (0,03 *104)+(0,98*104) = 1,01 * 104 = 0,101* 105
Пример 2.
(0,3333*103) - (0,331*103) = 0,002*103 = 0,2* 101
Порядок выполнения и особые случаи при сложении/вычитании чисел с плавающей запятой
- Определение разности порядков:
?П = Пx – Пy
Если ?П = +?, то Пx >> Пy, и Z = X.
Если ?П = -?, то Пy >> Пx, и Z = Y.
- Денормализация мантиссы числа с меньшим порядком:
Если ?П > 0, то Пx > Пy, Пz = Пx, M'y = My*2 - ?П, M'x = Mx.
Если ?П < 0, то Пy > Пx, Пz = Пy, M'x = Mx*2 - |?П|, M'y = My .
Если ?П = 0, то Пz = Пx = Пy. Денормализации мантисс не происходит: M'x = Mx, M'y = My.
- Алгебраическое суммирование чисел с равными порядками:
Mz = M'x ± M'y
Если |Мz| ? 1, то |M'z| =|Мz| * 2-1, П'z = Пz+1.
Если П'z = +?, то Z = ?.
Если П'z = -?, то Z = 0.
Приведем в качестве примера некоторые мантиссы (Табл. 10.1), представленные в различных кодах, и укажем, нормализованы ли они (+ означает нормализованную мантиссу, - ненормализованную).
| Двоичный код мантиссы числа | ПК | ОК | ДК |
|---|---|---|---|
| 0.101 | + | + | + |
| 1.101 | + | - | - |
| 0.010 | - | - | - |
| 1.010 | - | + | + |
| 0.100 | + | + | + |
| 1.100 | + | - | + |
Из анализа таблицы можно сделать вывод, что
- нормализованная мантисса, представленная в прямом коде, имеет первый знак после запятой, равный единице;
- нормализованная мантисса, представленная в обратном или дополнительном кодах, должна иметь первый знак после запятой, не совпадающий со знаковым разрядом. Исключение составляет число 1.10...0 для мантиссы в дополнительном коде.