НОУ ИНТУИТ | Элементы финансовой математики. Лекция 8: Операции с финансовыми контрактами

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.09.2017 | Доступ: свободный | Студентов: 1240 / 371 | Длительность: 12:18:00

Тема: Менеджмент

Специальности: Менеджер, Руководитель, Экономист

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.3 Выбор контракта покупателем

При покупке некоторого товара покупатель может заключить с продавцом контракт, включающий различные условия авансовой оплаты, получения кредита и сроков поставки товара. Чтобы выбрать наиболее выгодный для себя контракт, покупатель должен сравнить приведенные ценности возможных контрактов и найти контракт с наименьшей приведённой ценностью. Чтобы определить приведённую ценность платежей, необходимо принять какую-либо ставку сравнения, то есть ставку сложных процентов i, по которой будет производиться дисконтирование этих платежей. В теории корпоративных финансов рассматриваются различные подходы к выбору этой ставки. Рассмотрение этого вопроса выходит за рамки нашей книги.

При покупке товара покупатель делает платежи двух видов. Во-первых, это авансовые платежи 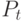$P_{t}$ , которые он выплачивает за купленный товар в моменты времени t (считая от момента заключения контракта) до поставки товара. Приведённая ценность этих платежей на момент заключения контракта вычисляется по формуле:

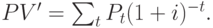
$PV'=\sum_{t} P_{t}(1+i)^{-t}.$

Во-вторых, это платежи по погашению кредита, равного разности между ценой товара C и суммой авансовых платежей:

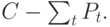
$C-\sum_{t} P_{t}.$

Приведённая ценность этих платежей зависит от условий погашения кредита. Пусть по контракту за кредит продавец получает g% годовых. Срок кредита (годы), который обычно отсчитывается от момента окончания поставки товара, обозначим через N. Рассмотрим два наиболее часто встречающихся случая:

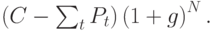
а) Кредит погашается разовым платежом в конце срока. Тогда сумма, выплачиваемая в конце срока кредита, вычисляется по формуле: $(C-\sum_{t} P_{t})\left(1+g\right)^{N}.$
Приведённая ценность этой суммы на момент заключения контракта вычисляется по формуле:

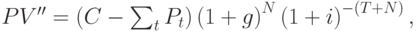
$PV''=(C-\sum_{t} P_{t})\left(1+g\right)^{N}\left(1+i\right)^{-(T+N)},$
где t - срок поставки товара.

Приведённая ценность PV всех платежей по контракту на момент его заключения вычисляется по формуле:

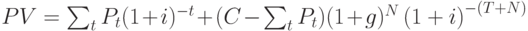
$PV=\sum_{t} P_{t}(1+i)^{-t}+(C-\sum_{t} P_{t})(1+g)^{N}\left(1+i\right)^{-(T+N)}$
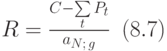
б) Кредит погашается равными срочными уплатами. Годовая срочная уплата R по выплате кредита вычисляется по формуле: $R={C-\sum\limits_{t} P_{t}\over a_{N;\,g}}\,\,\, (8.7)$
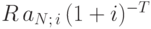Последовательность срочных уплат представляет собой ренту, состоящую из N платежей, равных R каждый. Приведённая ценность этой ренты в момент t по формуле из лекции 7 равна $R\,a_{N;\,i}$ . Приведённая ценность этой суммы в момент заключения контракта равна $R\,a_{N;\,i}\,(1+i)^{-T}$ . Следовательно, приведённая ценность всех платежей по контракту на момент его заключения вычисляется по формуле:

$PV=\sum_{t} P_{t}(1+i)^{-t}+(C-\sum_{t} P_{t})\,\frac{a_{N;\,i}}{a_{N;\,g}}\,\left(1+i\right)^{-T}\,\,\, (8.8)$

Рассмотрим пример на сравнение контрактов.

Пример 74. Сравним следующие два контракта при ставке сравнения 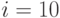i=10% .

1-й контракт: Цена товара равна 20 млн руб. Делается три авансовых платежа по 3 ~млн руб. каждый: первый - в момент заключения контракта, второй - через год, третий - ещё через год. Поставка товара производится сразу после авансовых платежей. Кредит предоставляется на 3 года, считая от момента поставки товара, под 15% годовых и погашается разовым платежом в конце срока кредита.

2-й контракт: Цена товара равна 181 млн руб. В момент заключения контракта делается один авансовый платеж, равный 5 млн руб. Поставка производится в момент заключения контракта. Кредит выдаётся на 5 лет под 15% годовых с погашением равными ежегодными уплатами.

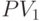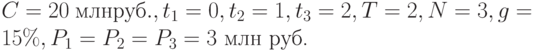Решение. Сравним приведенные ценности этих контрактов при i=10%. Для 1-го контракта $PV_{1}$ вычисляем по формуле (8.7) при $C=20~млн руб., t_{1}=0, t_{2}=1, t_{3}=2, T=2, N=3,g=15\%, P_{1}=P_{2}=P_{3}=3\mbox{ млн руб.}$ :

$PV_{1}= 3(1+i)^{0}+3(1+i)^{-1}+3(1+i)^{-2}+\\[4pt] +(20-9)(1+0.15)^{3}(1+0.1)^{-(2+3)}=\\[6pt] =3+3\times 1.1^{-1}+3\times 1.1^{-2}+11\times 1.15^{3}\times 1.1^{-5} = 18.594\mbox{ млн руб.}$

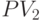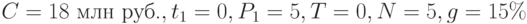Приведённую ценность 2-го контракта $PV_{2}$ вычисляем по формуле (8.8) при $C=18\mbox{ млн руб.}, t_{1}=0, P_{1}=5, T=0, N=5, g=15\%$ :

$PV_{2}=5(1+i)^{0}+(18-5)\,{a_{5;\,10\%}\over a_{5;\,15\%}}\,(1+i)^{0}=19.701 \mbox{~млн.\ руб.}$

Первый контракт более выгоден покупателю, чем второй, но он может предпочесть второй, так как поставка товара по нему производится немедленно, а по первому контракту - с отсрочкой на два года.

Дальше >>

Авторизоваться

Элементы финансовой математики

Операции с финансовыми контрактами

8.3 Выбор контракта покупателем

Вопросы и ответы