Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 410 / 20 | Длительность: 08:16:00
Темы: Экономика, Менеджмент
Лекция 4:
Рынок как система с ожиданием
4.9. Задача
Определить: соотношение потерь в полнодоступных группах емкостью 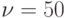 и
и 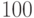 партий товаров, при системе с ожиданием при показательном распределении длительности занятия и по системе с потерями, при заданном значении потерь
партий товаров, при системе с ожиданием при показательном распределении длительности занятия и по системе с потерями, при заданном значении потерь  . Рассчитать:
. Рассчитать:
- среднее время ожидания для партий товаров, поступающих на рынок
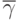
- среднее время ожидания товаров, находящихся в очереди,

- среднюю длину очереди

Решение. По таблицам первой формулы Эрланга при заданных величинах 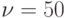 и
и 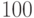 и
и 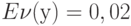 отыскиваем значения поступающего предложения
отыскиваем значения поступающего предложения  : при
: при 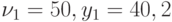 отн.ед.; при
отн.ед.; при 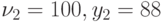 отн.ед.
отн.ед.
Используя (4.8) и полученные значения у, рассчитываем условные потери 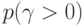 :
:

Для 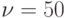
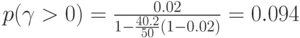
Для 
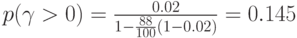
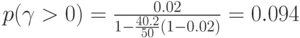
Среднее время ожидания для партий товаров, поступающих на рынок 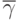 .
.
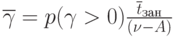
(предполагая, что 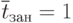 )
)
при 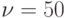 ;
; 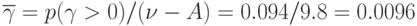 ,
,
при  ;
; 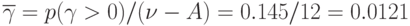
среднее время ожидания товаров, находящихся в очереди, 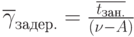
(предполагая, что 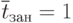 )
)
при 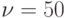 ;
; 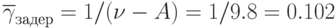
при  ;
; 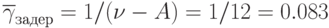
и среднюю длину очереди 
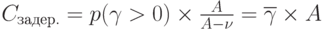
при 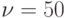 ;
; 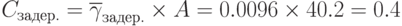
при  ;
; 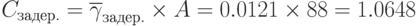
Приведенная задача показывает, что:
- дисциплина обслуживания по системе с ожиданием приводит к условным потерям, которые в несколько раз превышают явные потери, имеющие место при дисциплине обслуживания по системе с явными потерями;
- с увеличением емкости пучка линий при прочих равных условиях повышается отношение
 и ухудшаются показатели качества работы системы
и ухудшаются показатели качества работы системы 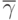 и
и 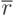 .
.
