|
Добрый день, при написании программы в Prologe появляется строчка getSpiral(_, _, _, _) = []. Но данный предикат нигде не описан и естественно программа выдае ошибку. Можно уточнить, что это за предикат и где и как его необходимо описать |
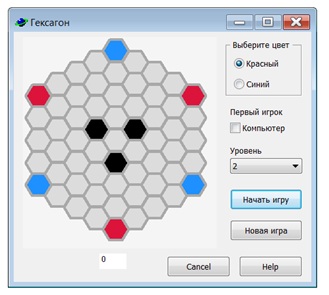
Игра "Гексагон"
Стратегия хода игрока
Ниже описываются правила игры и стратегия выбора хода игрока-компьютера.
Правила игры
Для игры используются фишки двух цветов — красные и синие. Один игрок ходит красными, другой синими. Изначально в угловые поля выкладываются по три фишки каждого цвета, цвета фишек в углах чередуются (рис. 10.1 рис. 10.1).
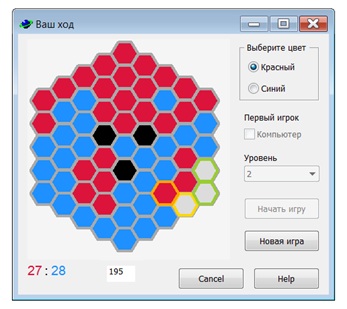
Ход игрока заключается в следующем. Игрок выбирает на доске фишку своего цвета и пустое поле, в которое он ходит (оба поля указываются с помощью клика мыши). Это поле должно быть расположено не далее чем через одно поле от выбранной фишки. На рис. 10.2 (a) рис. 10.2 ) доступные поля, в которые можно ходить, выделены желтым и зеленым цветами. Игрок может либо "удвоить" фишку — положить новую фишку на обозначенное желтым пустое поле, которое граничит с выбранной фишкой (рис. 10.2 (b) рис. 10.2 ), либо переместить выбранную фишку на выделенное зеленым пустое поле, которое расположено через одно поле (рис. 10.2 (c) рис. 10.2 ). Фишки противника, которые граничат с полем, в которое был сделан ход, захватываются — меняют свой цвет на цвет фишек игрока (рис. 10.2 (d) рис. 10.2 ). Игра заканчивается, когда очередной игрок не может сделать ход. Побеждает игрок, фишек которого на доске больше. В случае равного количества фишек признается ничья. Черным цветом помечены поля, в которые ходить нельзя.
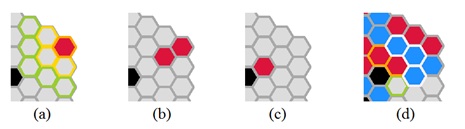
Рис. 10.2. (a) Доступные поля; (b) "удвоение" фишки; (c) перемещение фишки; (d) игрок красными ходит в соседнее поле и захватывает три синие фишки
Алгоритм альфа-бета отсечения
Успех применения к выбору хода компьютера таких алгоритмов, как алгоритма минимакса или алгоритма альфа-бета отсечения, обеспечивается тем, как оценивается позиция. Оценка позиции — это функция из множества позиций во множество действительных чисел. В данной игре используется простая оценочную функция: в качестве оценки позиции берется разница между количеством фишек игрока и количеством фишек противника.
Игрок-компьютер может играть на трех уровнях сложности. При игре на первом уровне сложности игрок-компьютер ходит так, чтобы оценка полученной позиции была максимальной. При игре на втором уровне сложности при выборе хода учитывается ответный ход пользователя, а при игре на третьем уровне — еще и последующий ход компьютера. На последних двух уровнях для выбора хода компьютера применяется алгоритм альфа-бета отсечения.
Алгоритм альфа-бета отсечения является модификацией алгоритма минимакса с помощью оценок, ограничивающих перебор ходов. Алгоритм минимакса обычно используют осторожные игроки, которые стремятся минимизировать потери (при этом подразумевается, что противник имеет тот же уровень, что и сам игрок). Поэтому опытный игрок может обыграть компьютер, но начинающему игроку это сделать не так просто.
Алгоритм минимакса заключается в следующем. Пусть P — текущая позиция в игре и ходит игрок X. Он может сделать ходы 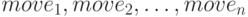 , в результате которых получатся позиции
, в результате которых получатся позиции 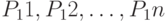 с оценками
с оценками 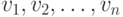 , соответственно (рис. 10.3
рис.
10.3). Будем считать, что
, соответственно (рис. 10.3
рис.
10.3). Будем считать, что 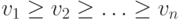 , так что v1 — максимальная оценка. Игрок-компьютер X, играющий на первом уровне сложности, выбирает ход move1.
, так что v1 — максимальная оценка. Игрок-компьютер X, играющий на первом уровне сложности, выбирает ход move1.
На втором уровне игрок X при выборе хода учитывает ответный ход его противника — игрока Y. Пусть ui — максимальная из оценок позиций Qij для игрока Y, в которые переходит игра из позиции Pi после хода игрока Y, для j = 1, 2, …, ki. Тогда минимальная из оценок позиций Qij для игрока X равна (– ui). Пусть при этом  . Соответственно, оценки позиций для игрока X удовлетворяют соотношению:
. Соответственно, оценки позиций для игрока X удовлетворяют соотношению:  . В соответствии с алгоритмом минимакса, игрок X выбирает ход moven. В результате его противник, как бы он ни ходил, может получить позицию с оценкой, равной самое большее un. Игроков X и Y называют Max и Min, соответственно. Первый игрок старается максимизировать свой выигрыш, учитывая, что второй игрок будет ходить так, чтобы его минимизировать.
. В соответствии с алгоритмом минимакса, игрок X выбирает ход moven. В результате его противник, как бы он ни ходил, может получить позицию с оценкой, равной самое большее un. Игроков X и Y называют Max и Min, соответственно. Первый игрок старается максимизировать свой выигрыш, учитывая, что второй игрок будет ходить так, чтобы его минимизировать.
На третьем уровне сложности игрок-компьютер учитывает еще один свой ход после хода противника. Пусть после хода в позиции Qij игрок X может получить позицию с оценкой самое большее wij. Пусть также  . Игрок Y, который также выбирает ход в соответствии с принципом минимакса, по изложенным выше причинам в позиции Pi выберет ход, приводящий к позиции
. Игрок Y, который также выбирает ход в соответствии с принципом минимакса, по изложенным выше причинам в позиции Pi выберет ход, приводящий к позиции  . Обозначим оценку
. Обозначим оценку 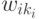 этой позиции через wi. Далее в приведенных выше рассуждениях следует заменить оценки (– ui) оценками (– wi), среди которых игрок X должен выбрать максимальную оценку. В результате игрок X получит позицию, оценка которой не хуже, чем оценка позиции при игре на втором уровне сложности, так как
этой позиции через wi. Далее в приведенных выше рассуждениях следует заменить оценки (– ui) оценками (– wi), среди которых игрок X должен выбрать максимальную оценку. В результате игрок X получит позицию, оценка которой не хуже, чем оценка позиции при игре на втором уровне сложности, так как  .
.
Алгоритм альфа-бета отсечения использует для ограничения перебора ходов оценки  и
и 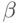 . Изначально значение оценки
. Изначально значение оценки  равно наименьшей возможной оценке позиции, а значение оценки
равно наименьшей возможной оценке позиции, а значение оценки 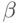 — наибольшей. Если в результате очередного хода игрока получается позиция, значение оценки v которой не меньше, чем значение оценки
— наибольшей. Если в результате очередного хода игрока получается позиция, значение оценки v которой не меньше, чем значение оценки 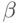 , то перебор ходов прекращается и выбирается данный ход. Если оценка v меньше, чем значение
, то перебор ходов прекращается и выбирается данный ход. Если оценка v меньше, чем значение 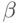 , но больше, чем значение
, но больше, чем значение  , то перебор ходов продолжается, но значение оценки
, то перебор ходов продолжается, но значение оценки  заменяется значением v. В противном случае перебор продолжается без изменения значения оценки
заменяется значением v. В противном случае перебор продолжается без изменения значения оценки  . По окончании перебора выбирается ход, приводящий к позиции с текущим значением оценки
. По окончании перебора выбирается ход, приводящий к позиции с текущим значением оценки  (см. ниже имплементацию класса compPlayer).
(см. ниже имплементацию класса compPlayer).
Системы координат для описания доски
Игровая доска состоит из шестиугольных полей, количество которых равно 61, включая три поля, в которые нельзя ходить по правилам игры. В программе поля являются правильными шестиугольниками.
Рассмотрим две системы координат, которые удобно использовать для описания доски.
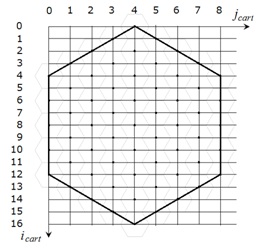
На рис. 10.4 рис. 10.4 показана система координат Oij. Она используется для представления шестиугольника в реализации игры. В ней шестиугольник описывается парой координат его центра (i, j).
Координаты центров шестиугольников в системе координат Oij являются целочисленными решениями системы неравенств: 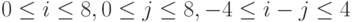 . Центры шестиугольников, в которые нельзя ходить по правилам игры, имеют координаты (3, 4), (4, 3) и (5, 5).
. Центры шестиугольников, в которые нельзя ходить по правилам игры, имеют координаты (3, 4), (4, 3) и (5, 5).
Положение шестиугольников в окне вычисляется с помощью декартовой системы координат  . Она показана на рис. 10.5
рис.
10.5.
. Она показана на рис. 10.5
рис.
10.5.
O'icartjcart
Если центр шестиугольника имеет координаты (i, j) в системе координат Oij, то его координаты (icart, jcart) в системе координат O'icartjcart находятся следующим образом:
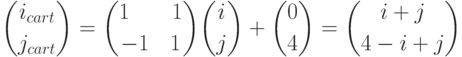
Пусть длина стороны шестиугольника равна s. Тогда расстояние между центрами соседних шестиугольников составляет по горизонтали 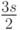 , по вертикали —
, по вертикали — 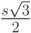 . Соответственно, если центр шестиугольника имеет координаты (icart, jcart) в системе координат O'icartjcart, то в системе координат окна его координаты находятся следующим образом:
. Соответственно, если центр шестиугольника имеет координаты (icart, jcart) в системе координат O'icartjcart, то в системе координат окна его координаты находятся следующим образом:
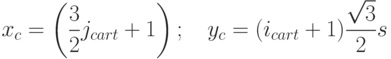
В программе дополнительно по обеим осям координат делается сдвиг на толщину границы шестиугольника.
Реализация игры
Создадим проект hexagonGame (MDI).
Создание формы
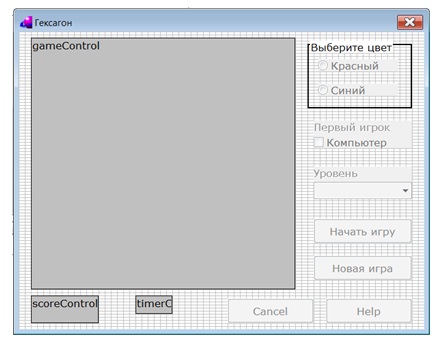
Прежде чем создавать окно, в котором размещается игровая доска, с помощью диалогового окна Create Project Item создадим два поля для рисования (DrawControl) и назовем их gameControl и scoreControl. Первое поле используется для создания доски, второе — для отображения текущего счета.
После этого создадим форму gameForm. Поместим в нее следующие элементы управления (рис. 10.6 рис. 10.6):
- пользовательский элемент управления (Custom Control):
- Class: gameControl,
- Right Anchor: True; Bottom Anchor: True (все якоря: True);
- пользовательский элемент управления (Custom Control):
- Class: scoreControl,
- Top Anchor: False; Bottom Anchor: True;
- пользовательский элемент управления (Custom Control):
- Class: timerControl,
- Top Anchor: False; Bottom Anchor: True; Text: 0;
- групповой блок (Group Box):
- Representation: Fact Variable;
- Name: color_ctl; Text: Выберите цвет;
- Left Anchor: False; Right Anchor: True;
- в групповом блоке нужно разместить переключатели (Radio Button):
- Name: red_ctl; Text: Красный; RadioState: checked;
- Name: blue_ctl; Text: Синий;
- надписи (Static Text) "Первый игрок", "Уровень":
- Left Anchor: False; Right Anchor: True;
- флажок (Check Box):
- Name: firstplayer_ctl; Text: Компьютер
- Left Anchor: False; Right Anchor: True;
- выпадающий список (List Button):
- Rows: 3, Left Anchor: False; Right Anchor: True;
- кнопки (Push Button):
- Name: start_ctl; Text: Начать игру;
- Name: restart_ctl; Text: Новая игра.
Для кнопок следует установить параметры:
- Left Anchor: False; Top Anchor: False;
- Right Anchor: True; Bottom Anchor: True.
Сделаем активным пункт меню File -> New, добавим обработчик события выбора данной команды меню и определим его так, как показано ниже:
clauses
onFileNew(_Source, _MenuTag):-
_ = gameForm::display(This).
Кроме этого, изменим определение предиката onShow в файле taskWindow.pro следующим образом:
clauses
onShow(_, _CreationData) :-
_MessageForm = messageForm::display(This),
_ = gameForm::display(This).
Домены и константы
Создадим интерфейс gameDomains и поместим в него объявления доменов и констант. Домен hex представляет поле (в системе координат Oij); домен position — позицию (списки полей компьютера и человека); домен nbr — тип "соседнего" поля (граничит ли оно с исходным или располагается через одно поле); домен move — ход (из какого поля, в какое поле и тип этого поля).
open core, vpiDomains
domains
hex = tuple{integer I, integer J}.
position = position(hex* CompHex, hex* HumanHex).
nbr = nbr1; nbr2. % тип соседства: рядом или через одно
move = move(hex From, hex To, nbr); nil.
constants
humanWinMes = "Вы выиграли!".
compWinMes = "Компьютер выиграл!".
drawMes = "Ничья!".
scoreMes = "Счет % : %".
constants
blackHex : hex* = [tuple(3, 4), tuple(4, 3), tuple(5, 5)].
initBlueHex : hex* = [tuple(0, 0), tuple(4, 8), tuple(8, 4)].
initRedHex : hex* = [tuple(0, 4), tuple(4, 0), tuple(8, 8)].
constants
redColor : color = color_Crimson.
blueColor : color = color_DodgerBlue.
blackColor : color = color_Black.
emptyColor : color = color_Gainsboro.
borderColor : color = color_DarkGray.
selectedColor : color = color_Orange.
neighborColor : color = color_Gold.
neighbor2Color : color = color_YellowGreen.
movedColor : color = color_Aquamarine.
captColor : color = color_LavenderBlush.
constants
comp = 0.
human = 1.
constants
borderWidth = 4.
Листинг
10.1.
Объявление доменов и констант
Шестиугольное поле
Создадим класс hexagon для описания шестиугольника. В интерфейс hexagon поместим объявление свойства hex, предиката calcCenter/1, вычисляющего координаты его центра, предиката pntInHex/1, истинного, если заданная точка лежит внутри шестиугольника, и предикатов polygon и smallPolygon, возвращающих координаты вершин шестиугольника, а также вершин шестиугольника меньшего размера. Второй шестиугольник используется для подсветки ходов.
properties
hex : gameDomains::hex.
predicates
calcCenter: (integer Size).
pntInHex: (vpiDomains::pnt) determ.
predicates
polygon: () -> vpiDomains::pnt*.
smallPolygon: () -> vpiDomains::pnt*.
Листинг
10.2.
Объявления в интерфейсе hexagon
Декларация класса содержит объявление конструктора.
constructors
new: (gameDomains::hex, integer Icart, integer Jcart).
Листинг
10.3.
Объявление конструктора в декларации класса hexagon
Ниже приведена имплементация класса hexagon.
open core, vpiDomains, gameDomains
facts
hex : hex.
icart : integer. % декартовы координаты
jcart : integer.
xc : integer := 0. % координаты центра
yc : integer := 0.
size : integer := 10. % длина стороны
clauses
new(Hex, Icart, Jcart):-
hex := Hex,
icart := Icart,
jcart := Jcart.
calcCenter(Size):-
size := Size,
xc := math::round((1.5 * jcart + 1) * size + borderWidth),
yc := math::round(
(icart + 1) * size * math::sqrt(3)/2 + borderWidth).
pntInHex(pnt(X, Y)):-
math::abs(X - xc)^2 + math::abs(Y - yc)^2 <= 3*(size^2)/4.
clauses
polygon() = [
pnt(xc - size, yc), pnt(Xa, Ya), pnt(Xb, Ya),
pnt(xc + size, yc), pnt(Xb, Yd), pnt(Xa, Yd)
]:-
Xa = math::round(xc - size/2), Xb = Xa + size,
H = size * math::sqrt(3)/2,
Ya = math::round(yc - H), Yd = math::round(yc + H).
smallPolygon() = [
pnt(X1 + 2, Y1), pnt(X2 + 1, Y2 + 1), pnt(X3 - 1, Y3 + 1),
pnt(X4 - 2, Y4), pnt(X5 - 1, Y5 - 1), pnt(X6 + 1, Y6 - 1)
]:-
[pnt(X1, Y1), pnt(X2, Y2), pnt(X3, Y3),
pnt(X4, Y4), pnt(X5, Y5), pnt(X6, Y6)] == polygon().
Листинг
10.4.
Определение в имплементации класса hexagon
Вычисление соседних полей
Для определения операции вычисления "соседних" полей используем отдельный класс (не порождающий объекты).
Создадим класс neighbors. В его декларации объявим предикаты, которые для заданного поля недетерминированно возвращают поле, граничащее с заданным полем или расположенное через одно поле.
open core, gameDomains
predicates
neighbor: (hex) -> hex nondeterm.
neighbor2: (hex) -> hex nondeterm.
!
Ниже приведено определение предикатов.
Листинг 10.6. Определение в имплементации класса neighbors
open core, gameDomains
clauses
neighbor(Hex) = NextHex:-
NextHex = neighbor_nd(Hex),
inBoard(NextHex).
neighbor2(Hex) = NextHex:-
NextHex = neighbor2_nd(Hex),
inBoard(NextHex).
class predicates
neighbor_nd: (hex) -> hex nondeterm.
inBoard: (hex) determ.
neighbor2_nd: (hex) -> hex nondeterm.
clauses
neighbor_nd(tuple(I, J)) =
tuple(I, J + std::fromToInStep(-1, 1, 2)). % J - 1 и J + 1
neighbor_nd(tuple(I, J)) = tuple(I + Di, J + Dj):-
Di = std::fromToInStep(-1, 1, 2), % Di = -1 и 1
Dj = std::between(0, Di). % Dj = 0 и -1, или Dj = 0 и 1
inBoard(tuple(I, J)):-
I >= 0, I <= 8,
J >= 0, J <= 8,
math::abs(J - I) <= 4.
neighbor2_nd(tuple(I, J)) =
tuple(I, J + std::fromToInStep(-2, 2, 4)). % J - 2 и J + 2
neighbor2_nd(tuple(I, J)) = tuple(I + Di, J + Dj):-
Di = std::fromToInStep(-2, 2, 4), % Di = -2 и 2
Dj = std::between(0, Di). % Dj = 0 и -2, или Dj = 0 и 2
neighbor2_nd(tuple(I, J)) = tuple(I + Di, J + Dj):-
Di = std::fromToInStep(-1, 1, 2), % Di = -1 и 1
Dj = std::betweenInStep(-Di, 2 * Di, 3). % Dj = 1 и -2,
% или Dj = -1 и 2
Листинг
10.5.
Объявление предикатов в декларации класса neighbors
Вывод текущих сообщений
Добавим вывод счета игры и сообщения об игроке, который должен ходить, а также вывод времени в секундах, прошедшего с начала игры (рис. 10.7 рис. 10.7).
Добавим в интерфейс scoreControl следующее объявление.
predicates
setScore: (string, vpiDomains::color, string, vpiDomains::color).
clear: ().
Листинг
10.7.
Объявление в интерфейсе scoreControl
В имплементации класса scoreControl изменим определение конструктора new/0 (установим шрифт) и определим объявленные предикаты.
clauses
new():-
userControlSupport::new(),
generatedInitialize(),
Font = vpi::fontCreateByName("@Arial Unicode MS", 12),
setFont(Font).
facts
info : tuple{string, charCount, color, string, color} := erroneous.
clauses
setScore(S1, Color1, S2, Color2):-
info := tuple(S1, string::length(S1), Color1, S2, Color2),
invalidate().
clear():-
info := erroneous,
invalidate().
Листинг
10.8.
Определение в имплементации класса scoreControl
Добавим в редакторе окна scoreControl.ctl обработчики событий PaintResponder и SizeListener и определим их так, как показано ниже.
clauses
onPaint(_Source, _Rectangle, GDI):-
not(isErroneous(info)),
tuple(S1, N, Color1, S2, Color2) = info,
!,
GDI:setForeColor(Color1),
GDI:drawText(pnt(20 - 10 * N, 15), S1),
GDI:setForeColor(color_Black),
GDI:drawText(pnt(25, 15), ":"),
GDI:setForeColor(Color2),
GDI:drawText(pnt(35, 15), S2).
onPaint(_Source, _Rectangle, _GDI).
clauses
onSize(_Source):-
invalidate().
Листинг
10.9.
Определение предикатов onPaint и onSize
Теперь объявим в интерфейсе gameForm предикаты вывода информации.
predicates
setMessage: (string).
setScore: (string, vpiDomains::color, string, vpiDomains::color).
timerStop: ().
Листинг
10.10.
Объявление предикатов в интерфейсе gameForm
В имплементации класса gameForm определим эти предикаты, а также изменим определение конструктора new/1 и добавим вспомогательные предикаты.
clauses
new(Parent):-
formWindow::new(Parent),
generatedInitialize(),
listButton_ctl:addList(["1", "2", "3"]),
listButton_ctl:selectAt(1, true),
timerControl_ctl:setTickDuration(1000). % 1000 = 1 с
facts
n : positive := 0. % длительность игры в секундах
clauses
setMessage(String):-
setText(String).
setScore(HumPoints, HumColor, Points, Color):-
scoreControl_ctl:setScore(HumPoints, HumColor, Points, Color).
timerStop():-
timerControl_ctl:stop().
predicates
setEnable: (boolean).
clauses
setEnable(Enabled):-
color_ctl:setEnabled(Enabled),
firstplayer_ctl:setEnabled(Enabled),
start_ctl:setEnabled(Enabled),
listButton_ctl:setEnabled(Enabled).
predicates
stoneColor: (boolean IsRed, color Human [out], color Comp [out]).
clauses
stoneColor(true, gameDomains::redColor,
gameDomains::blueColor):- !.
stoneColor(_, gameDomains::blueColor, gameDomains::redColor).
Листинг
10.11.
Определение в имплементации класса gameForm
Ниже создаются основные классы. Методы объектов одних классов используются в других классах, поэтому при компиляции будут возникать ошибки до тех пор, пока не будут определены все классы.
Создание игровой доски
Игровая доска создается в классе board. Игровая доска состоит из шестиугольных полей и располагается на игровом поле. Поэтому объект класса board взаимодействует с объектами класса hexagon и объектом класса gameControl.
Размеры шестиугольника и, соответственно, размеры всей доски определяются размерами игрового поля.
Создадим класс board. В интерфейс board добавим следующее объявление.
open core, vpiDomains, gameDomains
predicates
create: ().
update: ().
pntInHex: (pnt, hex) determ.
predicates
drawBoard: (windowGDI).
highlight: (windowGDI, tuple{hex From, hex* Nbr1, hex* Nbr2}).
showHex: (windowGDI, hex, color Pen, color Brush).
showNeighbors: (windowGDI, hex, hex*).
Листинг
10.12.
Объявление предикатов в интерфейсе board
Предикат create создает доску, состоящую из шестиугольных полей. Предикат update обновляет доску после изменения размеров окна. Предикат pntInHex/2 является истинным, если точка принадлежит шестиугольнику.
Предикат drawBoard/1 отображает доску. Предикат highlight/2 подсвечивает фишку, которой собирается пойти пользователь, а также поля, в которые он может пойти. Предикат showHex/4 отображает поле, из которого или в которое ходит игрок. Предикат showNeighbors/3 отображает захватываемые поля.
В декларации класса board объявим конструктор.
constructors
new: (gameControl).
Листинг
10.13.
Объявление конструктора в декларации класса board
Ниже приведено определение объявленных предикатов.
open core, vpiDomains, gameDomains
facts
gameCtl : gameControl := erroneous.
size : integer := 10. % сторона шестиугольника
facts
hex: (hex, hexagon).
clauses
new(GameCtl):-
gameCtl := GameCtl.
clauses
create():-
calcHexSize(),
createHexagons().
clauses
update():-
calcHexSize(),
calcHexCenters().
clauses
pntInHex(Point, Hex):-
hex(Hex, Hexagon),
!,
Hexagon:pntInHex(Point).
predicates
calcHexSize: ().
createHexagons: ().
calcHexCenters: ().
clauses
calcHexSize():-
gameCtl:getClientSize(W, H),
SizeX = W div 14,
SizeY = math::trunc((H - borderWidth)/(9 * math::sqrt(3))),
size := math::min(SizeX, SizeY).
createHexagons():-
I = std::fromTo(0, 8), J = std::fromTo(0, 8),
math::abs(I - J) <= 4,
Icart = I + J,
Jcart = 4 - I + J,
Hex = tuple(I, J),
Hexagon = hexagon::new(Hex, Icart, Jcart),
Hexagon:calcCenter(size),
assert(hex(Hex, Hexagon)),
fail.
createHexagons().
calcHexCenters():-
hex(_, Hexagon),
Hexagon:calcCenter(size),
fail.
calcHexCenters().
clauses % отображение доски
drawBoard(GDI):-
hex(_, Hexagon),
drawHexagon(GDI, gameCtl, Hexagon),
fail.
drawBoard(_GDI).
constants
small = 0.
normal = 1.
clauses % подсветка допустимых ходов
highlight(GDI, tuple(Hex, Nbrs1, Nbrs2)):-
drawHexList(GDI, Nbrs1, neighborColor),
drawHexList(GDI, Nbrs2, neighbor2Color),
drawHex(normal, GDI, Hex, selectedColor).
predicates
drawHexList: (windowGDI, hex*, color).
clauses
drawHexList(GDI, L, Color):-
list::forAll(L, {(Hex):- drawHex(small, GDI, Hex, Color)}).
clauses % отображение гексагона
showHex(GDI, Hex, PenColor, BrushColor):-
Polygon = hexagon(Hex):polygon(),
drawPolygon(GDI, Polygon, PenColor, BrushColor).
clauses % подсветка захватываемых фишек
showNeighbors(GDI, Hex, HexList):-
Nbr = neighbors::neighbor(Hex),
Nbr in HexList,
drawHex(normal, GDI, Nbr, captColor),
fail.
showNeighbors(_GDI, _Hex, _HexList).
predicates
drawHex: (positive, windowGDI, hex, color).
hexagon: (hex) -> hexagon.
polygon: (hexagon, positive) -> pnt*.
clauses
drawHex(Type, GDI, Hex, PenColor):-
Polygon = polygon(hexagon(Hex), Type),
drawPolygon(GDI, Polygon, PenColor, pat_Hollow, color_Black).
hexagon(Hex) = Hexagon:-
hex(Hex, Hexagon),
!.
hexagon(_Hex) = _:-
exception::raise_error().
polygon(Hexagon, small) = Hexagon:smallPolygon():- !.
polygon(Hexagon, _) = Hexagon:polygon().
class predicates
drawHexagon: (windowGDI, gameControl, hexagon).
drawPolygon: (windowGDI, pnt*, color, color).
drawPolygon: (windowGDI, pnt*, color, patStyle, color).
clauses
drawHexagon(GDI, Ctl, Hexagon):-
Polygon = Hexagon:polygon(),
BrushColor = Ctl:getColor(Hexagon:hex),
drawPolygon(GDI, Polygon, borderColor, BrushColor).
drawPolygon(GDI, Polygon, PenColor, BrushColor):-
drawPolygon(GDI, Polygon, PenColor, pat_Solid, BrushColor).
drawPolygon(GDI, Polygon, PenColor, PatStyle, BrushColor):-
GDI:setPen(pen(borderWidth, ps_Solid, PenColor)),
GDI:setBrush(brush(PatStyle, BrushColor)),
GDI:drawPolygon(Polygon).
Листинг
10.14.
Определение в имплементации класса board
Взаимодействие с игровым полем
Объект класса board взаимодействует с объектом класса gameControl, который, в свою очередь, взаимодействует с объектом класса game.
Добавим в интерфейс gameControl объявление свойств и предикатов.
properties
game : game (i).
board : board (o).
predicates
initPosition: ().
getColor: (gameDomains::hex) -> color.
showMove: (positive Player, gameDomains::move).
Листинг
10.15.
Объявление предикатов в интерфейсе gameControl
Предикат initPosition устанавливает исходную позицию в игре. Предикат getColor/1 возвращает цвет шестиугольного поля, как во время игры, так и в случае, когда игра еще не началась. Предикат showMove/2 используется для визуализации хода игрока.
В раздел open имплементации класса gameControl добавим имя интерфейса gameDomains:
open core, vpiDomains, gameDomains
Ниже приведено определение объявленных и вспомогательных предикатов и свойств.
facts
game : game := erroneous.
board : board := erroneous.
clauses
initPosition():-
game := erroneous,
invalidate().
clauses
getColor(Hex) = blackColor :-
Hex in blackHex,
!.
getColor(Hex) = game:getColor(Hex) :-
not(isErroneous(game)),
!.
getColor(Hex) = blueColor :-
Hex in initBlueHex,
!.
getColor(Hex) = redColor:-
Hex in initRedHex,
!.
getColor(_Hex) = emptyColor.
facts
timer: timerHandle := erroneous.
isHumanMove : boolean := false.
move : move := nil.
step : positive := 0.
penColor : color := borderColor.
brushColor : color := emptyColor.
clauses
showMove(Player, Move):-
game:playerPossibleMove := none(),
isHumanMove := toBoolean(human = Player),
move := Move,
invalidate(),
fail.
showMove(human, move(_, To, _)):- % захват фишек
neighbors::neighbor(To) in game:hexList(comp),
!,
timer := timerSet(500).
showMove(human, _):- !, % переход хода
nextMove(comp).
showMove(_comp, _Move):-
penColor := game:borderColor(comp),
brushColor := game:stoneColor(comp),
step := 3,
timer := timerSet(500).
predicates
nextMove: (positive Player).
nextPlayer: (boolean IsHumanMove) -> positive Player.
clauses
nextMove(Player):- % переход хода
move := nil,
game:move(Player).
nextPlayer(true) = comp. % следующий игрок
nextPlayer(false) = human.
predicates
moveIsPossible: () determ. % можно ходить
clauses
moveIsPossible():-
not(isErroneous(game)),
nil = move.
Листинг
10.16.
Определение в имплементации класса gameControl
В редакторе окна gameControl.ctl добавим обработчики событий ShowListener, SizeListener, PaintResponder, EraseBackgroundResponder, MouseDownListener и TimerListener.
Ниже приведено определение предиката onShow: создается доска.
clauses
onShow(_Source, _Data):-
board := board::new(This),
board:create().
Листинг
10.17.
Создание игровой доски
При изменении размеров окна игровая доска обновляется.
clauses
onSize(_Source):-
board:update(),
invalidate().
Листинг
10.18.
Обновление игровой доски
Для создания изображения доски используется холст.
Ниже определяется предикат onPaint. В первом правиле строится изображение доски. Остальные правила используются для визуализации ходов.
clauses
onPaint(_Source, _Rectangle, GDI):-
getClientSize(W, H),
Canvas = pictureCanvas::new(W, H),
Canvas:clear(color_WhiteSmoke),
board:drawBoard(Canvas), % изображение доски
GDI:pictDraw(Canvas:getPicture(), pnt(0, 0), rop_SrcCopy),
fail.
% подсветка допустимых ходов человека
onPaint(_Source, _Rectangle, GDI):-
not(isErroneous(game)),
HexNeighbors = tryGetSome(game:playerPossibleMove),
!,
board:highlight(GDI, HexNeighbors).
% подсветка хода человека, если он захватывает фишки
onPaint(_Source, _Rectangle, GDI):-
true = isHumanMove,
move(_, To, _) = move,
!,
board:showHex(GDI, To, game:borderColor(human),
game:stoneColor(human)),
board:showNeighbors(GDI, To, game:hexList(comp)).
% подсветка фишки, которой ходит компьютер
onPaint(_Source, _Rectangle, GDI):-
2 = step,
move(From, _, _) = move,
!,
board:showHex(GDI, From, penColor, brushColor).
% подсветка хода компьютера
onPaint(_Source, _Rectangle, GDI):-
1 = step,
move(From, To, NbrType) = move,
!,
if nbr2 = NbrType then
board:showHex(GDI, From, borderColor, emptyColor)
end if,
board:showHex(GDI, To, penColor, brushColor),
board:showNeighbors(GDI, To, game:hexList(human)).
onPaint(_Source, _Rectangle, _GDI).
Листинг
10.19.
Определение предиката onPaint
Предикат onEraseBackground определяется так же, как и ранее:
clauses
onEraseBackground(_Source, _GDI) = noEraseBackground.
Игрок-человек должен последовательно указать с помощью мыши фишку, которой он ходит, и поле, в которое он ходит. Ниже определяется предикат onMouseDown.
clauses
onMouseDown(_Source, Point, _ShiftControlAlt, _Button):-
moveIsPossible(),
game:startHumanMove(Point),
!.
onMouseDown(_Source, Point, _ShiftControlAlt, _Button):-
moveIsPossible(),
game:finishHumanMove(Point),
!.
onMouseDown(_Source, _Point, _ShiftControlAlt, _Button).
Листинг
10.20.
Определение предиката onMouseDown
Ниже определяется предикат onTimer.
clauses
onTimer(_Source, _Timer):-
false = isHumanMove,
step := step - 1,
step > 0,
!,
invalidate().
onTimer(_Source, _Timer):-
timerKill(timer),
timer := erroneous,
nextMove(nextPlayer(isHumanMove)).
Листинг
10.21.
Определение предиката onTimer
По окончании визуализации ход передается другому игроку.
Ход игрока
Ниже создается класс player, а также наследуемые классы humanPlayer и compPlayer. В классе player описываются свойства игрока и определяется ход игрока, Объекты классов humanPlayer и compPlayer взаимодействуют с объектом класса game.
Создадим класс player. В интерфейс player добавим объявление свойств и предикатов.
properties
game : game.
isFirst : boolean. % ходит ли первым
stoneColor : vpiDomains::color. % цвет фишек
level : integer. % уровень
hexList : gameDomains::hex*. % список фишек
moveMessage : string (o). % кто ходит
predicates
setInitHex: (). % начальная позиция
move: (). % обработка хода
makeMove: (). % выполнение хода
announceMove: (). % объявление о ходе
Листинг
10.22.
Объявление свойств и предикатов в интерфейсе player
Ниже приведена имплементация класса player.
open core, gameDomains
facts
game : game := erroneous.
isFirst : boolean := true.
stoneColor : vpiDomains::color := redColor.
level : integer := 0.
hexList : hex* := [].
moveMessage : string := "Ваш ход".
clauses
setInitHex():-
redColor = This:stoneColor,
!,
This:hexList := initRedHex.
setInitHex():-
This:hexList := initBlueHex.
announceMove():-
game:setMessage(This:moveMessage).
move():-
game:updatePosition(),
game:gameOver(This),
!.
move():-
This:announceMove(),
false = game:waiting,
!,
makeMove().
move().
makeMove():-
This:makeMove().
Листинг
10.23.
Определение в имплементации класса player
Теперь создадим класс humanPlayer с интерфейсом player. Выделим папку player дерева проекта и выберем пункт New In Existing Package всплывающего меню. В диалоговом окне Create Ptoject Item снимем флажок в поле Create Interface и в поле Name напишем имя класса humanPlayer. В декларации класса humanPlayer укажем имя интерфейса player так, как показано ниже.
class humanPlayer : player
open core
end class humanPlayer
Листинг
10.24.
Декларация класса humanPlayer
Ниже приводится полностью имплементация класса humanPlayer.
implement humanPlayer
open core, gameDomains
inherits player
clauses
makeMove():-
From in hexList,
game:movableHex(From),
NbrL1 = [Nbr1 || Nbr1 = neighbors::neighbor(From),
game:isEmpty(Nbr1)],
NbrL2 = [Nbr2 || Nbr2 = neighbors::neighbor2(From),
game:isEmpty(Nbr2)],
not(([] = NbrL1, [] = NbrL2)),
!,
game:highlightNeighbors(tuple(From, NbrL1, NbrL2)),
game:isPossibleMove := true.
makeMove():-
true = game:isPossibleMove,
some(tuple(From, NbrL1, NbrL2)) = game:playerPossibleMove,
(Nbr = nbr1, To in NbrL1; Nbr = nbr2, To in NbrL2),
game:movableHex(To),
!,
game:isPossibleMove := false,
game:updatePosition(This, move(From, To, Nbr)).
makeMove().
end implement humanPlayer
Листинг
10.25.
Имплементация класса humanPlayer
В имплементации класса humanPlayer определяется только предикат makeMove, который реализует выполнение хода игроком-человеком. В первом правиле находится поле, из которого делается ход, а также допустимые поля, в которые игрок может сделать ход, и вызывается предикат подсветки этих полей. Во втором правиле ход завершается — определяется поле, в которое делается ход, и вызывается предикат обновления позиции.
Далее точно так же следует создать класс compPlayer с интерфейсом player. Соответственно, потребуется внести изменение в декларацию класса compPlayer — указать имя интерфейса:
class compPlayer : player
Ниже приводится имплементация класса compPlayer. Определяются свойства игрока-компьютера и предикат makeMove. Напомним, что на первом уровне сложности ход выполняется так, чтобы оценка позиции была как можно больше. На втором и третьем уровне для выбора хода используется алгоритм альфа-бета отсечения. В качестве начальных значений оценок альфа и бета, равных минимальной и максимальной оценкам позиции, берутся значения (– 58) и 58, соответственно (количество полей на доске равно 58).
Предикат getMoves/1 возвращает список возможных ходов в виде троек tuple(Value, Position, Move), где Move — ход игрока, Position — позиция, к которой он приводит, и Value — оценка этой позиции, равная разности количества фишек игрока и количества фишек противника.
Список возможных ходов упорядочивается по убыванию оценок позиций, к которым они приводят (см. предикат alphaBeta/6), после этого начинается перебор ходов с целью выбора наилучшего (см. предикат bestMove/7).
Позиция представляется двумя списками — списком полей, занятых игроком, и списком полей, занятых противником. Поэтому в реализации хода противника достаточно поменять списки местами. Кроме этого, отметим, что если минимальная и максимальная оценки позиции игрока равны  и
и 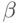 , то минимальная и максимальная оценки позиции противника равны, соответственно, (
, то минимальная и максимальная оценки позиции противника равны, соответственно, (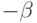 ) и (
) и (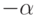 ). Далее, если позиция противника имеет оценку Value, то позиция игрока имеет значение (– Value).
). Далее, если позиция противника имеет оценку Value, то позиция игрока имеет значение (– Value).
Если оценка полученной позиции не меньше, чем бета, то ход найден (см. предикат tryBetaPruning/9). В противном случае делается попытка улучшить оценку альфа — заменить оценкой текущей позиции, если она превышает оценку альфа (см. предикат tryIncreaseAlpha/6), и перебор ходов продолжается. По окончании перебора оценка позиции полагается равной текущему значению оценки альфа.
implement compPlayer
open core, game, gameDomains
inherits player
facts
isFirst : boolean := false.
stoneColor : vpiDomains::color := blueColor.
level : integer := 1.
moveMessage : string := "Xод компьютера".
clauses
makeMove():-
Position = game:currentPosition,
Move = move(Position),
game:updatePosition(This, Move).
predicates
move: (position) -> move.
clauses
move(Position) = Move:-
level > 1,
alphaBeta(level, Position, -58, 58, Move, _),
!.
move(Position) = Move:-
Moves = getMoves(Position),
Moves <> [],
!,
tuple(_, _, Move) = list::maximum(Moves).
move(_Position) = _:-
exception::raise_error().
class predicates
alphaBeta: (integer, position, integer, integer, move [out],
integer [out]) nondeterm.
bestMove: (tuple{integer, position, move}*, integer, integer,
integer, move, move [out], integer [out]) nondeterm.
tryBetaPruning: (move, integer, integer, integer, integer,
tuple{integer, position, move}*, move, move [out],
integer [out]) nondeterm.
tryIncreaseAlpha: (move, move, integer, integer, move [out],
integer [out]).
clauses
alphaBeta(D, Position, Alpha, Beta, Move, Value):-
D > 0,
MoveList = getMoves(Position),
Moves = list::sort(MoveList, descending()),
bestMove(Moves, D - 1, Alpha, Beta, nil, Move, Value).
alphaBeta(0, Position, _, _, nil, value(Position)).
bestMove([tuple(_, Position, Move) | Moves], D, Alpha, Beta,
CurrMove, BestMove, BestValue):-
alphaBeta(D, invert(Position), -Beta, -Alpha, _, Value),
tryBetaPruning(Move, -Value, D, Alpha, Beta, Moves, CurrMove,
BestMove, BestValue).
bestMove([], _, Alpha, _, Move, Move, Alpha).
tryBetaPruning(Move, Value, _, _, Beta, _, _, Move, Value):-
Value >= Beta,
!.
tryBetaPruning(Move, Value, D, Alpha, Beta, Moves, CurrMove,
BestMove, BestValue):-
tryIncreaseAlpha(Move, CurrMove, Value, Alpha,
CurrMove1, Alpha1),
bestMove(Moves, D, Alpha1, Beta, CurrMove1, BestMove,
BestValue).
tryIncreaseAlpha(Move, _, Value, Alpha, Move, Value):-
Value > Alpha,
!.
tryIncreaseAlpha(_, CurrMove, _, Alpha, CurrMove, Alpha).
end implement compPlayer
Листинг
10.26.
Имплементация класса compPlayer
При выборе хода с помощью алгоритма альфа-бета отсечения, игрок-компьютер оценивает возможные ходы игрока-противника. Но он учитывает только один или два следующих хода, в зависимости от уровня, на котором играет, поэтому достаточно сильный игрок может его обыграть. При игре на первом уровне сложности ответные ходы противника не учитываются, поэтому обыграть его существенно проще.
Ход игры
Создадим класс game. Объект этого класса взаимодействует с объектами классов gameControl, gameForm, compPlayer и humanPlayer.
В интерфейс game поместим объявления свойств и предикатов.
open core, vpiDomains, gameDomains
properties
humanPlayer : player.
compPlayer : player.
currentPosition : position. % текущая позиция
isGameOver : boolean. % окончена ли игра
gameCtl : gameControl.
point : pnt. % координаты точки кас. кур.
isPossibleMove : boolean. % возможен ли ход
waiting : boolean.
playerPossibleMove: optional{tuple{hex, hex* Nbr1, hex* Nbr2}}.
predicates
startGame: ().
updatePosition: ().
updatePosition: (player, move).
gameOver: (player) determ.
isEmpty: (hex) determ.
getColor: (hex) -> color.
setMessage: (string).
move: (positive Player).
startHumanMove: (pnt) determ.
finishHumanMove: (pnt) determ.
movableHex: (hex) determ.
highlightNeighbors: (tuple{hex, hex* Nbr1, hex* Nbr2}).
borderColor: (positive Player) -> color PenColor.
stoneColor: (positive Player) -> color BrushColor.
hexList: (positive Player) -> hex*.
!
В декларации класса game также объявим ряд предикатов.
Листинг 10.28. Объявление предикатов в декларации класса game
open core, gameDomains
constructors
new: (player Human, player Comp, gameControl, gameForm).
predicates % находит все возможные ходы игрока
getMoves: (position) -> tuple{integer, position, move}*.
predicates % возвращает оценку позиции
value: (position) -> integer.
predicates % возвращает позицию противника
invert: (position) -> position.
Листинг
10.27.
Объявление свойств и предикатов в интерфейсе game
Следующий код следует поместить в имплементацию класса game.
open core, vpiDomains, gameDomains
facts
gameCtl : gameControl.
gameFrm : gameForm.
humanPlayer : player := erroneous.
compPlayer : player := erroneous.
currentPosition : position := position([], []).
isGameOver : boolean := true.
facts
point : pnt := erroneous.
isPossibleMove : boolean := false.
waiting : boolean := false.
playerPossibleMove : optional{tuple{hex, hex*, hex*}} := none().
clauses
new(Human, Comp, GameCtl, GameFrm):-
humanPlayer := Human,
compPlayer := Comp,
humanPlayer:game := This,
compPlayer:game := This,
gameCtl := GameCtl,
gameFrm := GameFrm.
clauses
getMoves(Position) = [
tuple(value(NextPosition), NextPosition, Move) ||
Move = move_nd(Position),
NextPosition = insert(Move, Position)].
class predicates
move_nd: (position) -> move nondeterm.
next: (hex From, hex To [out], nbr [out]) nondeterm.
clauses
move_nd(position(RL, BL)) = move(From, To, Nbr):-
From in RL,
next(From, To, Nbr),
isEmpty(To, RL, BL).
next(From, neighbors::neighbor(From), nbr1).
next(From, neighbors::neighbor2(From), nbr2).
class predicates
isEmpty: (hex, hex*, hex*) determ.
clauses
isEmpty(Hex, RL, BL):-
not(Hex in blackHex),
not(Hex in RL),
not(Hex in BL).
class predicates
insert: (move, position) -> position.
clauses
insert(move(From, To, Nbr), position(RL,BL))= position(RL2,BL2):-
RL1 = updateRL(Nbr, From, RL),
FromBL = [Hex || Hex = neighbors::neighbor(To), Hex in BL],
RL2 = list::sort([To | list::append(FromBL, RL1)]),
BL2 = updateBL(BL, FromBL).
insert(nil, Position) = Position.
class predicates
updateRL: (nbr, hex, hex*) -> hex*.
updateBL: (hex*, hex*) -> hex*.
clauses
updateRL(nbr1, _, RL) = RL:- !.
updateRL(_, From, RL) = list::remove(RL, From).
updateBL(BL, []) = BL:- !.
updateBL(BL, FromBL) = list::difference(BL, FromBL).
clauses
value(position(RL, BL)) = list::length(RL) - list::length(BL).
clauses
invert(position(RL, BL)) = position(BL, RL).
clauses
startGame():-
humanPlayer:setInitHex(),
compPlayer:setInitHex(),
currentPosition :=
position(compPlayer:hexList, humanPlayer:hexList),
fail.
startGame():-
true = humanPlayer:isFirst,
!,
isGameOver := false,
humanPlayer:announceMove().
startGame():-
compPlayer:move(),
isGameOver := false.
clauses
updatePosition():-
position(CompHex, HumanHex) = currentPosition,
humanPlayer:hexList := HumanHex,
compPlayer:hexList := CompHex,
gameCtl:invalidate().
updatePosition(Player, Move):-
OldPosition = playerPosition(Player),
Position = insert(Move, OldPosition),
currentPosition := playerPosition(Player, Position),
gameCtl:showMove(player(Player), Move).
predicates
playerPosition: (player) -> position.
playerPosition: (player, position) -> position.
player: (player) -> positive.
clauses
playerPosition(Player) = playerPosition(Player, currentPosition).
playerPosition(humanPlayer, Position) = invert(Position):- !.
playerPosition(_, Position) = Position.
player(humanPlayer) = human:- !.
player(_) = comp.
clauses
gameOver(Player):-
Position = playerPosition(Player),
not(_ = move_nd(Position)),
isGameOver := true,
gameFrm:timerStop(),
announceResult().
clauses
isEmpty(Hex):-
isEmpty(Hex, compPlayer:hexList, humanPlayer:hexList).
clauses
getColor(Hex) = humanPlayer:stoneColor :-
Hex in humanPlayer:hexList,
!.
getColor(Hex) = compPlayer:stoneColor :-
Hex in compPlayer:hexList,
!.
getColor(_Hex) = emptyColor.
clauses
setMessage(Message):-
gameFrm:setMessage(Message),
HumanPoints = list::length(humanPlayer:hexList),
CompPoints = list::length(compPlayer:hexList),
HumanColor = humanPlayer:stoneColor,
CompColor = compPlayer:stoneColor,
gameFrm:setScore(toString(HumanPoints), HumanColor,
toString(CompPoints), CompColor).
clauses
move(Player):-
waiting := toBoolean(human = Player),
toPlayer(Player):move().
predicates
toPlayer: (positive) -> player.
clauses
toPlayer(human) = humanPlayer:- !.
toPlayer(_) = compPlayer.
clauses
startHumanMove(Point):-
false = isGameOver,
humanMove(Point),
true = isPossibleMove.
finishHumanMove(Point):-
true = isPossibleMove,
humanMove(Point),
false = isPossibleMove.
predicates
humanMove: (pnt).
clauses
humanMove(Point):-
point := Point,
humanPlayer:makeMove().
clauses
movableHex(Hex):-
gameCtl:board:pntInHex(point, Hex).
clauses
highlightNeighbors(HexNeighbors):-
playerPossibleMove := some(HexNeighbors),
gameCtl:invalidate().
clauses
borderColor(human) = selectedColor:- !.
borderColor(_) = movedColor.
stoneColor(Player) = toPlayer(Player):stoneColor.
hexList(Player) = toPlayer(Player):hexList.
predicates
announceResult: ().
clauses
announceResult():-
CompPoints = list::length(compPlayer:hexList),
HumanPoints = list::length(humanPlayer:hexList),
Message = resultMessage(CompPoints, HumanPoints),
setMessage(Message).
class predicates
resultMessage: (integer CompPoints, integer HumPoints) -> string.
winMessage: (integer CompPoints, integer HumPoints) -> string.
scoreMessage: (integer CompPoints, integer HumPoints) -> string.
clauses
resultMessage(CP, HP) = string::format("% %", WMes, ScMes):-
WMes = winMessage(CP, HP),
ScMes = scoreMessage(CP, HP).
winMessage(Points, Points) = drawMes:- !.
winMessage(CompPoints, HumanPoints) = humanWinMes:-
HumanPoints > CompPoints,
!.
winMessage(_, _) = compWinMes.
scoreMessage(CP, HP) = string::format(scoreMes, P1, P2):-
[P1, P2] == list::sort([CP, HP]).
Листинг
10.29.
Определение в имплементации класса game
Создание игроков и начало игры
В редакторе формы gameForm добавим обработчики событий нажатия на кнопки "Начать игру" и "Новая игра", а также обработчик событий TickListener для поля timeControl_ctl.
Ниже приведено определение предикатов onStartClick, onRestartClick и onTimerControlTick.
clauses
onStartClick(_Source) = button::defaultAction:-
IsCompFirst = firstplayer_ctl:getChecked(),
[N | _] == listButton_ctl:getSelectedItems(),
Level = toTerm(integer, N),
Comp = compPlayer::new(),
Comp:isFirst := IsCompFirst,
Comp:level := Level,
Human = humanPlayer::new(),
Human:isFirst := boolean::logicalNot(IsCompFirst),
IsRed = toBoolean(
radioButton::checked = red_ctl:getRadioState()),
stoneColor(IsRed, HumanStoneColor, CompStoneColor),
Comp:stoneColor := CompStoneColor,
Human:stoneColor := HumanStoneColor,
Game = game::new(Human, Comp, gameControl_ctl, This),
gameControl_ctl:game := Game,
n := 0,
timerControl_ctl:setText("0"),
timerControl_ctl:start(),
Game:startGame(),
setEnable(false).
Листинг
10.30.
Определение предиката onStartClick
clauses
onRestartClick(_Source) = button::defaultAction:-
setEnable(true),
gameControl_ctl:initPosition(),
scoreControl_ctl:clear(),
setText("Гексагон"),
timerControl_ctl:setText("0"),
timerStop().
Листинг
10.31.
Определение предиката onRestartClick
predicates
onTimerControlTick : timerControl::tickListener.
clauses
onTimerControlTick(_Source):-
n := n + 1,
timerControl_ctl:setText(toString(n)).
Листинг
10.32.
Определение предиката onTimerControlTick
Упражнения
10.1. Создайте форму, содержащую таблицу результатов серии игр.
10.2. Реализуйте игру "Сапер" с демонстрацией ходов игрока-компьютера.
10.3. Реализуйте топологическую игру "Ползунок" на поле произвольного размера.
10.4. Реализуйте игру "Калах" [5 [ 5 ] ].
Заключение
Основные принципы программирования на современном декларативном языке Visual Prolog применяются к созданию компьютерных приложений.
Система Visual Prolog обладает хорошими возможностями для быстрого создания приложений в интегрированной среде разработки.
Возможности совместного использования с другими системами программирования позволяют все более расширять сферу применения языка Visual Prolog как в области научных исседований, так и в практической области.
В первой части пособия представлены основы логического программирования и языка Пролог, а также основы программирования на языка Visual Prolog. Во второй части приведены примеры создания приложений с графическим интерфейсом пользователя, в которых сочетается объектно-ориентированное программирование с логическим и функциональным. Умение создавать приложения и прототипы интеллектуальных систем полезно для будущих специалистов в области разработки прикладного программного обеспечения, в частности, интеллектуальных систем.