Задачи высшей математики с Maxima
3.4.3 Дифференцирование функций нескольких переменных
Для определения набора частных производных функции нескольких переменным (компонентов градиента) используется функция 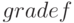 в формате
в формате 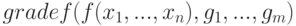 или
или 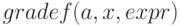
Выражение 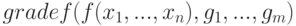 определяет
определяет 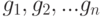 как частные производные функции
как частные производные функции 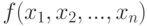 по переменным
по переменным 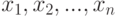 соответственно.
соответственно.
Зависимости между переменными можно явно указать при помощи функции  , которая позволяет декларировать, что переменная зависит от одной или нескольких других переменных. Например, если зависимость
, которая позволяет декларировать, что переменная зависит от одной или нескольких других переменных. Например, если зависимость  и
и  отсутствует, выражение
отсутствует, выражение 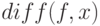 возвращает 0. Если декларировать её при помощи
возвращает 0. Если декларировать её при помощи  , выражение
, выражение 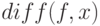 возвращает символьную производную.
возвращает символьную производную.
Пример:
(%i1) depends(y,x);
![[y\left( x\right) ]\leqno{(\%o1) }](/sites/default/files/tex_cache/d0fb0e3cd5c121d1c846c60cd374ce4f.png)
(%i2) gradef(f(x,y),x^2,g(x,y));

(%i3) diff(f(x,y),x);

(%i4) diff(f(x,y),y);

Вторая форма обращения к 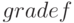 фактически устанавливает зависимость
фактически устанавливает зависимость  от
от  . При помощи
. При помощи 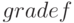 можно определить производные некоторой функции, даже если она сама неизвестна, посредством
можно определить производные некоторой функции, даже если она сама неизвестна, посредством 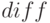 определить производные высших порядков.
определить производные высших порядков.
Для прямых вычислений, связанных с операциями векторного анализа, необходимо загрузить пакет vect. Кроме того, применения операторов 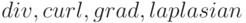 к некоторому выражению используется функция
к некоторому выражению используется функция  .
.
Пример: Вычисление градиента функции трех переменных
(%i2) grad (x^2 + 2*y^2 + 3*z^2);

(%i3) express(%);
![[\frac{d}{d\,x}\,\left( 3\,{z}^{2}+2\,{y}^{2}+{x}^{2}\right) ,\frac{d}{d\,y}\,\left( 3\,{z}^{2}+2\,{y}^{2}+{x}^{2}\right) ,\frac{d}{d\,z}\,\left( 3\,{z}^{2}+2\,{y}^{2}+{x}^{2}\right) ]\leqno{(\%o3) }](/sites/default/files/tex_cache/839437802b5d6536836031d73fafe373.png)
(%i4) ev(%,diff);
![[2\,x,4\,y,6\,z]\leqno{(\%o4) }](/sites/default/files/tex_cache/97bc059d8a742904d6cfa55b0bb49be4.png)
Вычисление дивергенции
(%i5) div([x^2,2*y^2,3*z^2]);
![div\left( [{x}^{2},2\,{y}^{2},3\,{z}^{2}]\right) \leqno{(\%o5) }](/sites/default/files/tex_cache/6f781cc2810b652e0d44c2156ad31554.png)
(%i6) express(%);
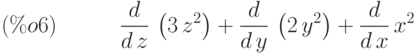
(%i7) ev(%,diff);

Вычисление вихря:
(%i8) curl([x^2,2*y^2,3*z^2]);
![curl\left( [{x}^{2},2\,{y}^{2},3\,{z}^{2}]\right) \leqno{(\%o8) }](/sites/default/files/tex_cache/5042bd2ef5ca29ecdebe156aec3bea7a.png)
(%i9) express(%);
![[\frac{d}{d\,y}\,\left( 3\,{z}^{2}\right) -\frac{d}{d\,z}\,\left( 2\,{y}^{2}\right) ,\frac{d}{d\,z}\,{x}^{2}-\frac{d}{d\,x}\,\left( 3\,{z}^{2}\right) ,\frac{d}{d\,x}\,\left( 2\,{y}^{2}\right) -\frac{d}{d\,y}\,{x}^{2}]\leqno{(\%o9) }](/sites/default/files/tex_cache/68b7d5273cff2d0c964196d9fdfb2cda.png)
(%i10) ev(%,diff);
![[0,0,0]\leqno{(\%o10) }](/sites/default/files/tex_cache/d39ae7d10dc57b5729a215cdf7816f63.png)
Вычисление оператора Лапласа:
(%i13) laplacian(x^2+2*y^2+3*z^2);
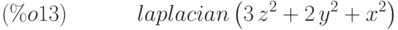
(%i14) express(%);
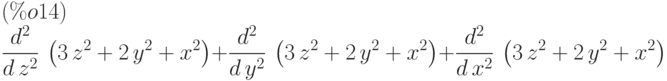
(%i15) ev(%,diff);

Рассмотрим пример исследования функции нескольких переменных: исследовать на экстремум функцию 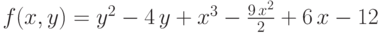
Загружаем пакет vect
(%i1) load("vect")$Определяем исследуемое выражение и вычисляем его градиент:
(%i2) f:x^3-9/2*x^2+6*x+y^2-4*y-12;
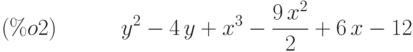
(%i3) grad(f);
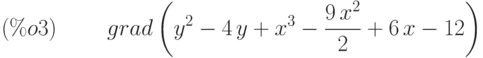
(%i4) express(%);
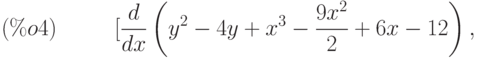
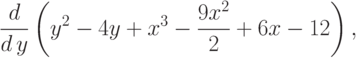
![\frac{d}{dz}\,\left( {y}^{2}-4y+{x}^{3}-\frac{9{x}^{2}}{2}+6x-12\right) ]](/sites/default/files/tex_cache/14c305e8c950dd47d02ea76cafd8efe2.png)
(%i5) ev(%,diff);
![[3\,{x}^{2}-9\,x+6,2\,y-4,0]\leqno{(\%o5) }](/sites/default/files/tex_cache/569369837319af5a4b7a26ea319750d7.png)
Выделяем из полученного списка частные производные и решаем систему 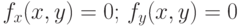
(%i6) dfdx:%o5[1];

(%i7) dfdy:%o5[2];

(%i8) solve([dfdx=0,dfdy=0],[x,y]);
![[[x=1,y=2],[x=2,y=2]]\leqno{(\%o8) }](/sites/default/files/tex_cache/7e9721b796e16642f91485c7129dff91.png)
В результате решения находим две критические точки 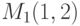 и
и 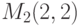 Для проверки, достигается ли в критических точках экстремум, используем достаточное условие экстремума:
Для проверки, достигается ли в критических точках экстремум, используем достаточное условие экстремума:
(%i9) A:diff(dfdx,x);

(%i10) C:diff(dfdy,y);

(%i11) B:diff(dfdx,y);

(%i12) A*C-B^2;

Так как 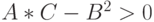 только в точке
только в точке 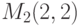 , то исследуемая функция имеет единственный экстремум. Учитывая, что в точке
, то исследуемая функция имеет единственный экстремум. Учитывая, что в точке 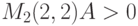 , точка
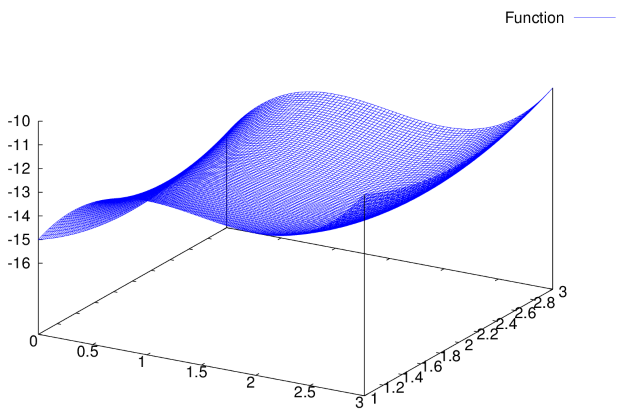
, точка  — точка минимума. Результат иллюстрируем графически рис. 3.13).
— точка минимума. Результат иллюстрируем графически рис. 3.13).