Нейроподобные модели как формально-логический базис анализа живых систем
8.4. PD-ассоциативные вычислительные конструкции как основа структурно-параметрического метода хранения и преобразования информации
В перспективной супрамолекулярной электронике высокодинамичная (ре)генерация супрамолекулярных гетероструктур станет неотъемлемым атрибутом вычислительного процесса, и осуществлять ее, возможно, придется после каждого цикла исполнения слов-инструкции, что приводит к совмещению во времени и пространстве процессов производства и эксплуатации супрамолекулярных гетероструктур. Такая постановка задачи выводит нас за рамки классических подходов к построению "надежных" вычислителей из "надежных" [70, 228, 237] или "ненадежных" [66, 238, 239] комп онент. Как было показано в предыдущих разделах, осуществить инструктированный синтез супрамолекулярных
гетероструктур можно только на основе методов и средств структурно-параметрической идентификации, которая требует учета содержимого как выполняемых инструкций, так и преобразуемых ими данных, от которых и будет зависеть "время жизни" активизированной супрамолекулярной гетероструктуры.
В традиционной опто- и микроэлектронике необходимость в использовании структурно-параметрических методов и средств хранения и преобразования информации не возникала из-за того, что здесь преобразование информации (потоков инструкций и данных) осуществляется на основе детерминированных булевых преобразований параметров электромагнитных, оптических, акустических и т. п. сигналов, которые распространяются по стабильным во времени гетероструктурам. При этом "информация" о самой гетероструктуре рассматривается как системотехническая, схемотехническая или конструкторско-технологическая и поэтому используется только при проектировании и изготовлении вычислителей, а не во время вычислений.
-
Системотехнические и схемотехнические соглашения, задающие структурно-функциональные возможности абстрактного, элементарного, молекулярного субстрата (в дальнейшем просто исходный молекулярный субстрат), введем исходя из апробированных в классической микроэлектронике [138] принципов и методов МКМД -бит-потоковой организации вычислений. В таких технологиях базовый принцип "одна (бит)инструк-ция - один (бит)процессор" строго выдерживается на всех уровнях организации вычислений: бит-процессорном, слов-процессорном и поток-процессорном (см. раздел 6.5).
Соподчиненный принцип регламентирует предельный потоковый режим организации вычислений, в котором процессы обработки и передачи данных совмещены по времени и аппаратуре, а их скорости равны. Оба этих процесса осуществляются в конвейерной арифметике обычно младшим разрядом вперед, а все бит-процессоры (сверх)большого коллектива работают синхронно.
Реализация этих принципов приводит к разделению во времени фазы программирования (сверх)большого бит-процессорного коллектива вычислителей с фазой вычислений и к закреплению за каждым бит-процессором единственной бит-инструкции, которую он исполняет "непрерывно" в течение всего времени активности потокового оператора.
Приведенные данные говорят о том, что требования такой вычислительной технологии адекватны условиям эффективного применения структурно-параметрических методов хранения и преобразования информации. Поэтому для переноса МКМД-бит-потоковой технологии микропрограммного конструирования в область супрамолекулярной электро-
ники требуется повысить темп работы инструментальных платформ и включить их в состав системных средств оперативного синтеза супрамо-лекулярных вычислителей. В итоге фаза структурной адаптации (сверх) большого коллектива микроэлектронных бит-процессоров заменяется фазой инструктированного синтеза супрамолекулярных МКМД-бит-потоковых гетероструктур.
Исходя из поставленной таким образом задачи, будем считать, что исходный молекулярный субстрат:
- имеет операционный канал и канал транзита (табл. 8.5), в первом из которых реализуется бит-операция "арифметическая сумма" (
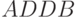 ), а во втором можно осуществить транзитную передачу одного потока входных операндов в двух произвольных направлениях [138, 140];
), а во втором можно осуществить транзитную передачу одного потока входных операндов в двух произвольных направлениях [138, 140]; - может взаимодействовать по четырем возможным ортогональным направлениям приема и передачи потоков данных по одноразрядным "безынерционным" шинам.
Топология "конструктивных" соединений исходного молекулярного субстрата в супрамолекулярной гетероструктуре сохраняется только на ограниченном количестве циклов обработки входных операндов, но исходный субстрат при этом не разрушается и может быть использован в вычислителях-потомках. Передача и обработка информации в операционном канале и канале транзита исходного молекулярного субстрата осуществляются синхронно с обязательной или с дополнительной задержкой на 1 такт каждая.
Таблица 8.5. Условное графическое изображение бит-инструкций Условное изображение Комментарий В операционном канале АЭМС выполняется сложение двух операндов, поступающих на нулевом такте слева и снизу. Результирующий операнд выдается на первом такте вправо. В канале транзита входной операнд поступает на нулевом такте снизу и с задержкой на один такт подается вверх, а с задержкой на два такта (*) - вниз. АЭМС реализует только ветвление входного операнда, пришедшего на нулевом такте слева, передавая его вниз с задержкой на 1 такт и вправо с задержкой на 2 такта (*). Операционный канал не используется (отсутствует). Дополнительная задержка обозначена звездочкой (*). Воспользуемся PD -ассоциативной формой представления реализуемой исходным молекулярным субстратом арифметико-логической функции потокового суммирования
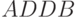 (см. раздел 5.3):
(см. раздел 5.3):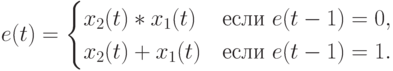
( 8.10) 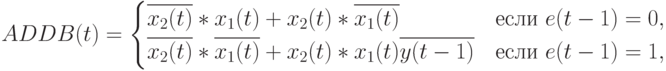
( 8.11) где
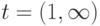 - целочисленное время,
- целочисленное время,  - входные переменные, а символы (
- входные переменные, а символы (  ), (
), ( 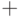 ) и (
) и (  ) соответствуют
) соответствуют 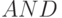 ,
, 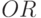 и
и 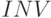 (инверсии) соответственно.
(инверсии) соответственно.Такая форма представления раскрывает используемые на "вентильном уровне" неразрушающие ассоциативные механизмы "сверхбыстрого" переключения с одной "элементарной" функции на другую. В результате в супрамолекулярной электронике ассоциативное управление реализуемыми функциями можно осуществить с помощью содержимого обрабатываемых или специально сформированных потоков данных, конформационно изменяющих вторичную и/или третичную структуру "рабочего тела".
В случае (8.10) и (8.11) PD -ассоциативная переключательная конструкция проявляется в том, что содержимое "единицы переноса" на предыдущем такте
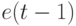 управляет правилом формирования "единица переноса" на текущем такте
управляет правилом формирования "единица переноса" на текущем такте  либо как бит-операция
либо как бит-операция 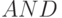 , либо как бит-операция
, либо как бит-операция 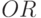 . Аналогично для "арифметической суммы"
. Аналогично для "арифметической суммы" 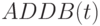 , которая реализуется либо как
, которая реализуется либо как  , либо как
, либо как 
Классические DD -ассоциативные конструкции [46] "маскирование"
 , "маскирование с инверсией"
, "маскирование с инверсией"  или "маскирование с условной инверсией"
или "маскирование с условной инверсией"  также можно представить в PD -ассоциативной форме:
также можно представить в PD -ассоциативной форме: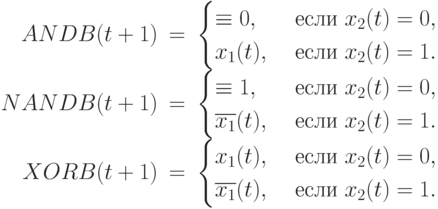
( 8.12) где ассоциативной для пользователя считается "внешняя" по отношению к исходному молекулярному субстрату и поэтому доступная ему переменная
 .
.Соотношения (8.12) раскрывают механизмы PD -ассоциативной потоковой реализации логических функций
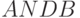 ,
, 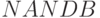 и
и 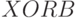 , в качестве которых в супрамолекулярной электронике могут выступать как конформационные преобразования молекул, сохраняющие неизменными "конструктивные" связи супрамолекулярных гетероструктур , так и высокодинамичные реакции замещения молекул, зависящие от некоторого комплекса внешних условий, "кодируемых"
, в качестве которых в супрамолекулярной электронике могут выступать как конформационные преобразования молекул, сохраняющие неизменными "конструктивные" связи супрамолекулярных гетероструктур , так и высокодинамичные реакции замещения молекул, зависящие от некоторого комплекса внешних условий, "кодируемых"  . Поэтому "схемотехническая" ценность выражений (8.12) состоит в том, что в супрамолекулярной электронике для вычислительных нужд можно использовать как традиционные средства управления параметрами (значениями токов, интенсивностями потоков фотонов, напряжениями и т. п.), так и средства структурно-параметрической адаптации атомарных или (макро)молеку-лярных структур.
. Поэтому "схемотехническая" ценность выражений (8.12) состоит в том, что в супрамолекулярной электронике для вычислительных нужд можно использовать как традиционные средства управления параметрами (значениями токов, интенсивностями потоков фотонов, напряжениями и т. п.), так и средства структурно-параметрической адаптации атомарных или (макро)молеку-лярных структур.Из (8.12), в частности, следует, что для перехода от DD -ассоциативной формы записи к эквивалентной PD -ассоциативной форме записи достаточно воспользоваться разложением Шеннона булевых функций
 переменных:
переменных: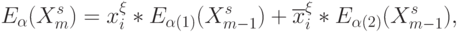
( 8.13) где выделенная "свободная" переменная
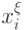 и ее инверсия
и ее инверсия 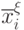 используются как управляющие, которые в темпе реального времени обеспечивают переход от
используются как управляющие, которые в темпе реального времени обеспечивают переход от 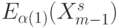 к
к 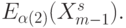
Продолжив процедуру (8.13) до
 переменных и далее, получим: в PD -ассоциативных конструкциях в качестве управляющих могут выступать не только отдельные переменные, но и вектора, с ростом размерности которых понижается уровень "элементарности" маскируемых ими функций. Отсюда, в супрамолекулярной электронике уровень деструкции "рабочего тела" вычислителя-предка тем глубже, чем выше размерность PD -ассоциативного управляющего вектора в вычислителе-потомке.
переменных и далее, получим: в PD -ассоциативных конструкциях в качестве управляющих могут выступать не только отдельные переменные, но и вектора, с ростом размерности которых понижается уровень "элементарности" маскируемых ими функций. Отсюда, в супрамолекулярной электронике уровень деструкции "рабочего тела" вычислителя-предка тем глубже, чем выше размерность PD -ассоциативного управляющего вектора в вычислителе-потомке. - имеет операционный канал и канал транзита (табл. 8.5), в первом из которых реализуется бит-операция "арифметическая сумма" (
-
PD-ассоциативные конструкции слов-процессорного уровня организации вычислений создаются микропрограммным конструированием супрамолекулярных гетероструктур, во время которого исходный молекулярный субстрат размещается в ячейки плоской решетки под управлением содержимого одного из обрабатываемых операндов, и после этого реализуют единственную закрепленную за каждым из них бит-инструкцию, включающую бит-операцию и все пересылки данных ортогональным соседям. Как и в реальных условиях, будем считать, что исходный молекулярный субстрат может выполнить закрепленную за ним функцию только в "контексте" своего размещения в супрамолекулярных гетероструктурах, то есть только при наличии соседей по топологии, указанных в микропрограмме. Но, будучи вырван из "контекста" конкретной топологической схемы, исходный молекулярный субстрат, вообще говоря, изменяет свою структурно-функциональную схему и реализуемую бит-инструкцию.
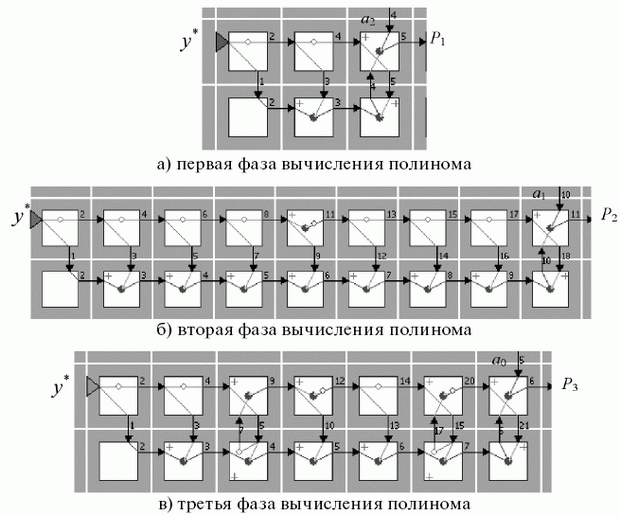
Для определенности совместим в пространстве и во времени инструктированный синтез PD -ассоциативных супрамолекулярных гетерострук-тур с вычислением полинома
 -й степени
-й степени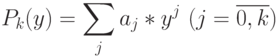
по известной схеме Горнера:
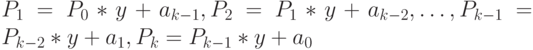 ,, где
,, где  . Переменную
. Переменную  и коэффициенты полинома
и коэффициенты полинома 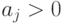 для простоты будем считать положительными целыми числами, заданными последовательным двоичным кодом разрядности
для простоты будем считать положительными целыми числами, заданными последовательным двоичным кодом разрядности  без знака.
без знака.Как и в любой систолической структуре [70], в супрамолекулярной гетероструктуре, реализующей схему Горнера, каждое фиксированное значение
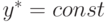 пробегает семейство из
пробегает семейство из  PD -ассоциативных (в данном случае конвейерных) умножителей, с той разницей, что топологическая схема таких умножителей зависит либо от содержимого аргумента
PD -ассоциативных (в данном случае конвейерных) умножителей, с той разницей, что топологическая схема таких умножителей зависит либо от содержимого аргумента 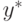 , либо от содержимого промежуточной переменной
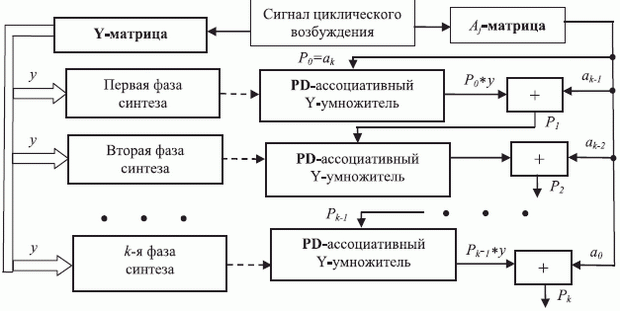
, либо от содержимого промежуточной переменной  . В первом случае (рис. 8.4) традиционная процедура инициализации слов-инструкций заменяется процедурой циклического синтеза специализированного операционного устройства по известной исполняемой операции и известному операнду
. В первом случае (рис. 8.4) традиционная процедура инициализации слов-инструкций заменяется процедурой циклического синтеза специализированного операционного устройства по известной исполняемой операции и известному операнду 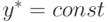 , который циклически (по
, который циклически (по  ) заносится в "тело" регенерируемого PD -ассоциативного
) заносится в "тело" регенерируемого PD -ассоциативного  -умножителя.
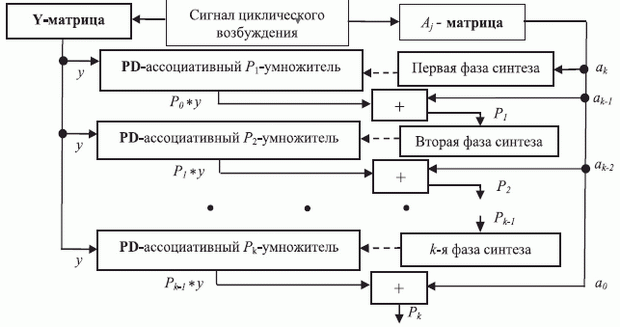
-умножителя.Во втором случае (рис. 8.5) на каждом
 -м цикле вычисления полинома синтезируется новая супрамолекулярная гетероструктура, в "тело" которой заносится содержимое промежуточной переменной
-м цикле вычисления полинома синтезируется новая супрамолекулярная гетероструктура, в "тело" которой заносится содержимое промежуточной переменной 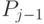 , что превращает ее в PD -ассоциативный
, что превращает ее в PD -ассоциативный  -умножитель.
-умножитель.Проиллюстрируем сказанное, зафиксировав параметры полинома и аргумента:
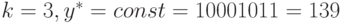 ;
; 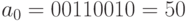 ;
; 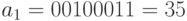 ;
; 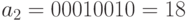 ;
; 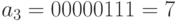 . Тогда:
. Тогда:  ;
;  ;
; 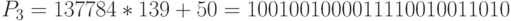 . Все операнды передаются и обрабатываются в последовательном коде младшим разрядом вперед.
. Все операнды передаются и обрабатываются в последовательном коде младшим разрядом вперед.Преимущество первой схемы: фазы регенеративного синтеза PD -ассоциативных
 -умножителей-потомков совмещаются во времени (векторизуются) с фазами вычислений в умножителях-предках, так как влияющий на топологическую схему супрамолекулярной гетерострук-туры операнд
-умножителей-потомков совмещаются во времени (векторизуются) с фазами вычислений в умножителях-предках, так как влияющий на топологическую схему супрамолекулярной гетерострук-туры операнд 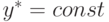 известен с самого начала вычисления полинома. Во втором случае фазы синтеза и использования PD -ассоциативных
известен с самого начала вычисления полинома. Во втором случае фазы синтеза и использования PD -ассоциативных  -умножителей чередуются во времени, но при этом каждый промежуточный
-умножителей чередуются во времени, но при этом каждый промежуточный  -операнд "хранится" в супрамолекулярной гетероструктуре, что позволяет приостановить вычислительный процесс на любом цикле вычисления полинома.
-операнд "хранится" в супрамолекулярной гетероструктуре, что позволяет приостановить вычислительный процесс на любом цикле вычисления полинома.В схеме рис. 8.4 PD -ассоциативные конвейерные
 -умножители выполняют операцию вида
-умножители выполняют операцию вида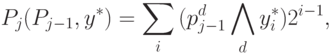
где
 - значение
- значение  -го бита множимого
-го бита множимого 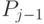 ;
; 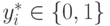 - значе-ние
- значе-ние  -го бита множителя, а
-го бита множителя, а  -
-  -битный оператор
-битный оператор 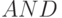 ,
, 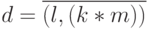 и
и 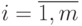 . Здесь ассоциативным операндом, определяющим структуру "сдвигов-сложений", служит аргумент
. Здесь ассоциативным операндом, определяющим структуру "сдвигов-сложений", служит аргумент  . Поэтому его содержимое задает структуру "сдвигов-сложений" множимого
. Поэтому его содержимое задает структуру "сдвигов-сложений" множимого  , а значит, и топологическую схему МКМД-бит-потокового
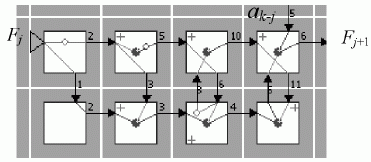
, а значит, и топологическую схему МКМД-бит-потокового  -умножителя (рис. 8.6 - в условных обозначениях табл. 8.5).
-умножителя (рис. 8.6 - в условных обозначениях табл. 8.5).В этой схеме цифрами обозначены времена задержки на входах-выходах исходного молекулярного субстрата, которые показывают, что временные сдвиги на входах молекулярного субстрата нижней, "суммирующей" строки как раз и определяются "расстоянием" между первым и остальными "единичными" битами операнда
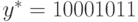 .
.При вычислении полинома по схеме рис. 8.5 множимое
 и множитель
и множитель 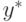 меняются ролями:
меняются ролями: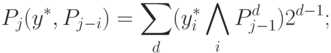
и поэтому синтез МКМД-бит-потокового
 -умножителя-потомка (рис. 8.7) можно начать только после появления первых двух значащих бит промежуточной переменной
-умножителя-потомка (рис. 8.7) можно начать только после появления первых двух значащих бит промежуточной переменной  на выходе
на выходе 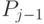 -умножителя-предка. В результате общее время задержки в схеме рисунка 4 может превысить в два и более раз время задержки в схеме рис. 8.4.
-умножителя-предка. В результате общее время задержки в схеме рисунка 4 может превысить в два и более раз время задержки в схеме рис. 8.4.Из приведенных данных видно:
- В технике схему инструктированного синтеза биополимеров можно воспроизвести с использованием нейроподобных многопороговых моделей и механизмов, а также при наличии PD -ассоциативной структурно-функциональной памяти, создаваемой по технологии постоянных ЗУ, а используемой по технологии ассоциативных ЗУ.
- В PD -ассоциативных супрамолекулярных гетероструктурах преобразование информации ведется в ассоциативной памяти инструкций, а не в ассоциативной памяти данных, причем PD -ассоциативные механизмы схемотехнического уровня обеспечивают "сверхбыстрое" управление переключением инструкций в ячейках супрамолекуляр-ной гетероструктуры, а на системном уровне они задают топологию синтезируемой супрамолекулярной гетероструктуры.
- В PD -ассоциативных вычислительных технологиях "время жизни" операционных устройств разного функционального назначения можно ограничить периодом активности исполняемой слов- или поток-инструкции.
- Как и в молекулярной биологии, синтез PD -ассоциативных супра-молекулярных гетероструктур предполагает наличие инструктирующих матриц, где хранятся переменные и параметры конкретных вычислительных схем, трансляцию и/или транскрипцию которых в адекватные гетероструктуры можно осуществить на основе многопороговых моделей. При этом синтез таких структур можно проводить как по классической схеме инструктированного синтеза макромолекул нативного белка (
 -умножители), так и по эпигенетической схеме синтеза прионов (
-умножители), так и по эпигенетической схеме синтеза прионов (  -умножители-потомки).
-умножители-потомки). - Топология PD -ассоциативных супрамолекулярных вычислительных устройств даже при выполнении ими одной и той же функции существенно зависит от содержимого одного из операндов, который используется как ассоциативная управляющая переменная в инструктированном синтезе таких устройств.
- Минимаксное "время жизни" абстрактных супрамолекулярных гете-роструктур (минимально необходимое для ассоциативного операнда максимальной разрядности) в обеих схемах определяется соотношением
![T = [(k+1)*m+2]\tau_{c}](/sites/default/files/tex_cache/2a641566bed1ee98ccd54ea6c07f9ce1.png) , только в
, только в  -умножителях время задержки неизменно и в пределе составляет
-умножителях время задержки неизменно и в пределе составляет 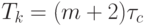 , а время вычисления
, а время вычисления  -операндов варьирует и в пределе составляет
-операндов варьирует и в пределе составляет  . В
. В  -умножителях времена задержки и вычислений меняются ролями с точностью до константы
-умножителях времена задержки и вычислений меняются ролями с точностью до константы 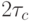 , где
, где 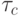 - цикл синхронизации супрамо-лекулярной гетероструктуры.
- цикл синхронизации супрамо-лекулярной гетероструктуры. - Несмотря на строгую алгоритмическую ориентированность и жесткую структурно-функциональную схему, все абстрактные супрамо-лекулярные гетероструктуры обладают традиционным для вычислительной техники структурно-функциональным полиморфизмом. В частности, при
 и
и 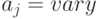 эти структуры реализуют базовое выражение
эти структуры реализуют базовое выражение  , а при
, а при 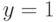 ,
, 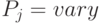 и
и 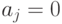 они работают как обычные ячейки памяти, содержимое которых (в данном случае это
они работают как обычные ячейки памяти, содержимое которых (в данном случае это  ) идентифицируется слабой неразрушающей переменной
) идентифицируется слабой неразрушающей переменной 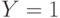 .
.