Теория вычислений и машины Тьюринга
3.1. Интуитивные предпосылки формализации понятия "алгоритм"
Негативные последствия внушительных успехов микроэлектроники и вычислительной техники выражаются в том, что с середины 70-х годов прошлого столетия они стали развиваться в заметном отрыве от достижений теории вычислений. Хорошо апробированный на практике операционный базис ЭВМ классической архитектуры допускал такой разрыв между теорией и практикой. Но ситуация кардинальным образом изменилась из-за отсутствия видимого прогресса в промышленном освоении нанотехнологий, где так и не удается решить проблему декоге-рентизации квантового "рабочего тела", вызванного рассеянием тепловой энергии, что приводит к неоднозначной реализации требуемых функций и, как следствие, к потере управления ходом вычислительного процесса. Проблему декогерентизации можно решить двумя путями:
- комплексом физико-технических мер, стабилизирующих на продолжительных временных интервалах (порядка 10 тыс. часов и выше) соответствие между структурой и функцией квантового "рабочего тела", чем, собственно, и занимаются физико-технические лаборатории во всем мире;
- адаптацией методов организации вычислений под условия квазиустойчивой реализации требуемых функций квантовым "рабочим телом". Первый путь полностью сохраняет традиционные методы и средства
организации вычислений, а с ним и наработанное программное обеспечение, которые должны поддерживаться физико-техническими и схемотехническими решениями, устойчивыми к внешним воздействующим факторам на "бесконечных" интервалах времени.
Второй путь требует признания квантовых реалий и пересмотра основополагающих принципов организации вычислений, а значит, и более углубленного анализа достижений теории вычислений.
Центральное место в этой теории занимает понятие "алгоритм", без которого не может обойтись и вычислительная техника. Вызвано это тем, что использование ЭВМ, начиная с классической фон-неймановской архитектуры, становится возможным только в том случае, если решаемая задача представлена в формализованном виде, то есть частично упорядоченной последовательностью арифметико-логических операций, которые
способна выполнить конкретная ЭВМ. Сам термин происходит от имени арабского математика Мохаммеда ибн Мусса Альхваризми (IX век).
Под разрешающим алгоритмом в математике понимают общее правило решения задач из некоторого класса, которое можно найти за конечное число шагов, без эвристики и чисто механически, если само решение существует [45].
О разрешающем алгоритме приходится говорить не только при решении класса задач, но и в случае выполнения одной арифметико-логической операции (суммирование, умножение, сравнение и т. п.), которая в конечном счете представляет собой последовательность правил использования преобразований двоек или троек символов, входящих в упорядоченные последовательности, именуемые числами. В частности, сложение двух целых десятичных чисел 327 и 458 (327 + 458 = 785) можно выполнить по следующему алгоритму:
Шаг 1. Присвоить индексу 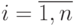 значение, отвечающее первому члену натурального ряда
значение, отвечающее первому члену натурального ряда 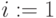 , и выделить в слагаемых первые справа символы
, и выделить в слагаемых первые справа символы 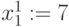 и
и 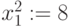 , где нижний индекс
, где нижний индекс  соответствует положению суммируемых символов в упорядоченной последовательности (номер разряда). По таблице подстановки, отвечающей правилу суммирования (табл. 3.1), выбрать символы 5 и 1, где символ 5 соответствует значению первого разряда "суммы" (
соответствует положению суммируемых символов в упорядоченной последовательности (номер разряда). По таблице подстановки, отвечающей правилу суммирования (табл. 3.1), выбрать символы 5 и 1, где символ 5 соответствует значению первого разряда "суммы" ( 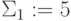 ), а символ 1 - значению "единицы переноса" (
), а символ 1 - значению "единицы переноса" ( 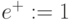 ) во второй разряд. Если
) во второй разряд. Если  не последний член натурального ряда (
не последний член натурального ряда ( 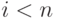 ), то выполнить шаг 2. В противном случае (при
), то выполнить шаг 2. В противном случае (при 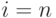 ) перейти к шагу 3.
) перейти к шагу 3.

|
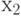
|

|

|
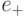
|

|
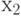
|

|

|
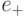
|

|
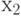
|

|

|
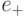
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | 6 | 0 | |||||
| 0 | 1 | 0 | 1 | 0 | 1 | 9 | 1 | 1 | 1 | 3 | 4 | 0 | 7 | 0 |
| 2 | 2 | 0 | 4 | 0 | ||||||||||
| 0 | 9 | 0 | 9 | 0 | 2 | 3 | 0 | 5 | 0 | 3 | 9 | 0 | 2 | 1 |
| 0 | 0 | 1 | 1 | 0 | ||||||||||
| 0 | 1 | 1 | 2 | 0 | 2 | 5 | 0 | 7 | 0 | 3 | 3 | 1 | 7 | 0 |
| 3 | 4 | 1 | 8 | 0 | ||||||||||
| 0 | 9 | 1 | 0 | 1 | 2 | 9 | 0 | 1 | 1 | |||||
| 1 | 1 | 0 | 2 | 0 | 2 | 2 | 1 | 5 | 0 | 3 | 9 | 1 | 3 | 1 |
| 1 | 2 | 0 | 3 | 0 | 2 | 3 | 1 | 6 | 0 | |||||
| 2 | 4 | 1 | 7 | 0 | ||||||||||
| 1 | 9 | 0 | 0 | 1 | 2 | 5 | 1 | 8 | 0 | 7 | 7 | 0 | 4 | 1 |
| 1 | 1 | 1 | 3 | 0 | 7 | 8 | 0 | 5 | 1 | |||||
| 1 | 2 | 1 | 4 | 0 | 2 | 9 | 1 | 2 | 1 |
Шаг 2. Присвоить индексу  значение следующего члена натурального ряда
значение следующего члена натурального ряда 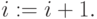 (Здесь
(Здесь  не действие, а условное обозначение непосредственно следующего члена натурального ряда, стоящего за
не действие, а условное обозначение непосредственно следующего члена натурального ряда, стоящего за  ). Выделить в слагаемых символы из (
). Выделить в слагаемых символы из (  )-го разряда (в данном случае это
)-го разряда (в данном случае это 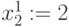 и
и 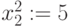 ).
С учетом значения символа "единица переноса" от предыдущего разряда (
).
С учетом значения символа "единица переноса" от предыдущего разряда ( 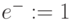 ) по таблице подстановки выбрать символы 8 и 0, где символ 8 соответствует значению второго разряда "суммы" (
) по таблице подстановки выбрать символы 8 и 0, где символ 8 соответствует значению второго разряда "суммы" ( 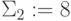 ), а символ 0 - значению символа "единица переноса" (
), а символ 0 - значению символа "единица переноса" (  ) в (
) в (  )-й разряд. Если символ
)-й разряд. Если символ  не последний член натурального ряда (
не последний член натурального ряда ( 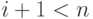 ), то повторить шаг 2. В противном случае (при
), то повторить шаг 2. В противном случае (при 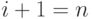 ) выполнить шаг 3.
) выполнить шаг 3.
В нашем случае повторяем шаг 2, то есть  В выделенном разряде слагаемых расположены символы
В выделенном разряде слагаемых расположены символы 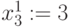 и
и 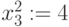 ,
которым с учетом значения символа "единица переноса" от предыдущего разряда
,
которым с учетом значения символа "единица переноса" от предыдущего разряда 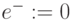 в таблице подстановки соответствуют символы
в таблице подстановки соответствуют символы 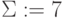 и
и 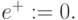 При этом выполняется условие
При этом выполняется условие 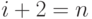 , что приводит к шагу 3.
, что приводит к шагу 3.
Шаг 3. Подставить в следующий разряд суммы значение символа "единица переноса". Конец алгоритма: сумма представляет собой упорядоченную последовательность символов 
Приведенных данных достаточно для следующих обобщений:
- Любой алгоритм предполагает перечисление некоторых действий (в случае вычислений - арифметико-логических операций), каждое из которых также выполняется по некоторому заранее заданному алгоритму, то есть задание алгоритма уже предполагает отношение иерархии, когда входящие в него действия также выполняются по некоторому алгоритму над некоторой совокупностью "элементарных действий".
- Отношение иерархии в алгоритмах предполагает некоторые исходные, определенные, но неопределяемые элементарные действия. В нашем случае это:
- ассоциативная выборка по содержимому данных из таблицы суммирования символов, которые априори известны, однозначно понимаемы и реализуемы на практике;
- подстановка символов в результирующую последовательность (операнд "сумма").
- Вне зависимости от уровня иерархии каждый алгоритм должен выполняться за конечное число шагов. В нашем случае на уровне алгоритма сложения количество шагов определяется разрядной сеткой ( n ) суммируемых переменных. На уровне "элементарных действий" количество шагов определяется многообразием значений триплетных символов
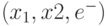 , индексирующих строки таблицы преобразования по закону суммирования триплетов входных символов в дуплеты выходных
, индексирующих строки таблицы преобразования по закону суммирования триплетов входных символов в дуплеты выходных 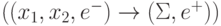 . Достоинство ассоциативной выборки пары (
. Достоинство ассоциативной выборки пары ( 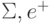 ) как раз и состоит в том, что она осуществляется за 1 шаг [46].
) как раз и состоит в том, что она осуществляется за 1 шаг [46]. - 4. Любой алгоритм можно остановить только по условию, но само условие может быть определено как свойство результата, который может быть получен либо с помощью данного алгоритма (например, наибольший общий делитель двух натуральных чисел в алгоритме Евклида), либо с помощью дополнительной процедуры, которая в нашем случае подразумевает достижение позиции, помеченной символом
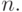
Следствие 3.1. Исходной "элементарной операцией", задающей в традиционной вычислительной технике правила суммирования, умножения, деления, сравнения и т. д., является ассоциативная выборка, которая характерна для нейроподобных вычислительных технологий и которая в скрытом виде реализуется на схемотехническом уровне организации работы классических ЭВМ начиная с фон-неймановской архитектуры.
Следствие 3.2. Программно-аппаратные платформы классических ЭВМ априори являются иерархическими и включают как минимум два уровня: "элементарных действий" и основанных на них арифметико-логических операций (в современной терминологии соответственно микрокомандный и ассемблерный).
Следствие 3.3. Любая задача, решаемая классической ЭВМ любой архитектуры, в конечном счете представлена в нейроподобном операционном базисе ассоциативной выборки и подстановки символов из некоторого конечного алфавита. Другими словами, если абстрагироваться от громоздкости описания, то нейроподобного операционного базиса достаточно для формального описания алгоритма решения любой вычислительной задачи, если такое решение существует.
Прогресс в развитии алгоритмических методов решения задач произошел задолго до появления ЭВМ и привел к тому, что такие математики, как Р. Декарт, Г. Лейбниц и Д. Гильберт, исходили из того, что решением любой поставленной математической задачи или проблемы должно быть ее алгоритмическое решение. Г. Лейбниц даже придумал приспособленную для этих целей автоматически работающую машину, которую не удалось реализовать на практике. Тем не менее вера в универсальность алгоритмических методов дожила до середины 30-х годов прошлого столетия, когда К. Гедель [47] доказал алгоритмическую неразрешимость некоторых математических проблем. Было показано, что известные математические проблемы невозможно разрешить с помощью алгоритмов из некоторого
точно определенного класса. Алгоритмическая разрешимость по К. Геделю зависит от степени совпадения этого точно определенного класса алгоритмов и класса всех интуитивно понимаемых алгоритмов. В результате пока математики, следуя Д. Гильберту, верили, что все поставленные математические задачи алгоритмически разрешимы, у них не было необходимости уточнять само понятие "алгоритм": раз с помощью некоторой совокупности правил решена некоторая математическая проблема, то этого уже было достаточно для того, чтобы считать совокупность использованных правил алгоритмом. Только утверждение об алгоритмической неразрешимости, которое оперирует со всеми мыслимыми алгоритмами, требует предварительного уточнения самого понятия "алгоритм".
Для преодоления возникшей логической коллизии был предложен целый ряд уточнений этого понятия, делающих его адекватным интуитивному пониманию термина "алгоритм". При этом удалось доказать эквивалентность всех уточнений на основе общерекурсивных функций (К. Гедель, С. Клини, 1934-1936),  -рекурсивных функций (К. Гедель, С. Клини, 1936),
-рекурсивных функций (К. Гедель, С. Клини, 1936),  -определимых функций (А. Черч, С. Клини, 1933-1936), машин Тьюринга (А. Тьюринг, Е. Пост, 1936), марковских алгоритмов (А. Марков, 1950), графических схем (Р. Петер, 1958) и т. п.
-определимых функций (А. Черч, С. Клини, 1933-1936), машин Тьюринга (А. Тьюринг, Е. Пост, 1936), марковских алгоритмов (А. Марков, 1950), графических схем (Р. Петер, 1958) и т. п.
Более того, оказалось, все алгоритмы в одном из точных смыслов являются алгоритмами в интуитивном смысле, а все известные алгоритмы можно "промоделировать" любым из алгоритмов в одном из точных смыслов.
Это позволило А. Черчу [48] сформулировать тезис о тождественности интуитивного понятия "алгоритм" с одним из эквивалентных между собой точных определений. Тезис Черча играет в математике ту же роль, что и второе начало термодинамики в физике, так как невозможно строго определить понятие "алгоритм" в интуитивном смысле.
В вычислительной технике наибольшее распространение получило уточнение понятия "алгоритм" на основе машин Тьюринга, которое исходит из следующих требований, лежащих в основе его интуитивного понимания.
Требование 1. Алгоритм оперирует с конструктивными объектами, над которыми можно выполнить заранее оговоренные операции.
Такие объекты, если они не являются словами над некоторым алфавитом  , можно перенумеровать элементами натурального ряда
, можно перенумеровать элементами натурального ряда  и затем оперировать не самими объектами, а их номерами (геделезация).
Поэтому в вычислительной технике в качестве конструктивных объектов можно рассматривать только слова, то есть конечные последовательности символов из некоторого алфавита
и затем оперировать не самими объектами, а их номерами (геделезация).
Поэтому в вычислительной технике в качестве конструктивных объектов можно рассматривать только слова, то есть конечные последовательности символов из некоторого алфавита  . Следуя [45], обозначим множество слов над
. Следуя [45], обозначим множество слов над  через
через 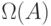 , которому принадлежит и "пустое" слово ( # ), то есть
, которому принадлежит и "пустое" слово ( # ), то есть 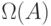 является полугруппой [49] с единичным элементом # по отношению к двуместной операции последовательного написания слов.
является полугруппой [49] с единичным элементом # по отношению к двуместной операции последовательного написания слов.
Требование 2. Алгоритм  задается конечным предписанием
задается конечным предписанием 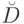 , входным алфавитом
, входным алфавитом  , выходным алфавитом
, выходным алфавитом  , содержащим
, содержащим  и
и  рабочим алфавитом
рабочим алфавитом  и размерным числом
и размерным числом 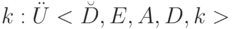 ,
где
,
где  - количество слов в последовательности слов, каждое из которых содержит
- количество слов в последовательности слов, каждое из которых содержит  символов из алфавита
символов из алфавита 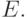
В соответствии с таким описанием алгоритм  можно применить к
можно применить к  -членной последовательности
-членной последовательности  слов над
слов над  Без нарушения общности ограничим рассмотрение алгоритмов на "микропрограммном" уровне организации вычислений, то есть будем считать
Без нарушения общности ограничим рассмотрение алгоритмов на "микропрограммном" уровне организации вычислений, то есть будем считать 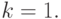
Говорят, что  применяется к
применяется к  , если
, если  является исходным объектом при выполнении операций, указанных в предписании
является исходным объектом при выполнении операций, указанных в предписании 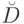 , с использованием рабочего алфавита
, с использованием рабочего алфавита  . Возможно, что согласно
. Возможно, что согласно 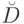 операции должны быть прекращены, после чего должно быть написано слово над
операции должны быть прекращены, после чего должно быть написано слово над  .
Если написанное слово является элементов
.
Если написанное слово является элементов 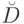 , то оно считается результатом применения алгоритма.
В противном случае его применение не приводит ни к какому результату. При этом считается, что само предписание
, то оно считается результатом применения алгоритма.
В противном случае его применение не приводит ни к какому результату. При этом считается, что само предписание 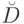 конечно, так как бесконечные предписания невозможно передать и зафиксировать.
конечно, так как бесконечные предписания невозможно передать и зафиксировать.
Требование 3. Предписание 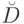 должно быть составлено так, чтобы определяемые им операции выполнялись поэтапно, то есть последовательно одна за другой. Согласно этому требованию предписание
должно быть составлено так, чтобы определяемые им операции выполнялись поэтапно, то есть последовательно одна за другой. Согласно этому требованию предписание 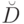 должно содержать не только описание операций, но и указания перехода от одной позиции к "следующей за ней".
должно содержать не только описание операций, но и указания перехода от одной позиции к "следующей за ней".
Требование 4. Предписание 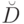 должно быть составлено так, чтобы его исполнение было однозначно и не допускало свободы принятия решений. Однозначность исполнения предписания необходима для создания технических устройств. В математике отказ от однозначности приводит к исчислению вместо алгоритма.
должно быть составлено так, чтобы его исполнение было однозначно и не допускало свободы принятия решений. Однозначность исполнения предписания необходима для создания технических устройств. В математике отказ от однозначности приводит к исчислению вместо алгоритма.
Требование 5. Предписание 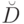 должно быть составлено так, чтобы его исполнение было воспроизводимо. Это предполагает следующее: применение алгоритма
должно быть составлено так, чтобы его исполнение было воспроизводимо. Это предполагает следующее: применение алгоритма  к одному и тому же слову приводит либо ни к какому, либо к одному и тому же результату. Данное требование исключает предписания с использованием вероятностного механизма выбора либо реализуемой операции, либо преобразуемого слова или символа.
к одному и тому же слову приводит либо ни к какому, либо к одному и тому же результату. Данное требование исключает предписания с использованием вероятностного механизма выбора либо реализуемой операции, либо преобразуемого слова или символа.
Требование 6. Предписание 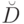 должно быть составлено так, чтобы его исполнение не требовало никакой другой информации, кроме той, которая содержится в исходном слове и в самом предписании.
должно быть составлено так, чтобы его исполнение не требовало никакой другой информации, кроме той, которая содержится в исходном слове и в самом предписании.
Требование 7. На длину предписания 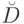 , длину слов, с которыми оно может оперировать, и число шагов, необходимых для его исполнения, не накладывается никаких других ограничений, кроме конечности, то есть соображения гиперкомбинаторных размерностей вычислений при теоретических исследованиях алгоритмов в расчет не принимаются.
, длину слов, с которыми оно может оперировать, и число шагов, необходимых для его исполнения, не накладывается никаких других ограничений, кроме конечности, то есть соображения гиперкомбинаторных размерностей вычислений при теоретических исследованиях алгоритмов в расчет не принимаются.
Требование 8. Предписание 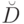 должно быть составлено так, чтобы исполняющему его вычислителю требовалась сколь угодно большая, но не бесконечная память.
должно быть составлено так, чтобы исполняющему его вычислителю требовалась сколь угодно большая, но не бесконечная память.
