|
Здравствуйте! Когда появится возможность сдать экзамен на сертификат? |
Опубликован: 08.11.2022 | Доступ: свободный | Студентов: 73 / 0 | Длительность: 06:05:00
Тема: Аппаратное обеспечение
Лекция 7:
Логические схемы на примере двоичного сумматора
Одноразрядный двоичный сумматор; четырехразрядный двоичный сумматор; оптимизация сумматора с целью ускорения переноса для арифметики большой разрядности; арифметико-логическое устройство (блок) процессора.
В этой лекции мы рассмотрим пример важной логической схемы - двоичного сумматора, который выполняет сложение двух чисел, представленных в двоичной системе исчисления.
Одноразрядный двоичный сумматор
Сначала рассмотрим одноразрядный сумматор, который позволяет складывать два бита. Для этого сначала вспомним алгоритм сложения "в столбик", универсальный для систем исчисления с любым основанием. Этот алгоритм предписывает складывать числа, начиная с младших разрядов, причём на входе каждого разряда, помимо слагаемых, есть ещё и перенос из предыдущего, равный 0 или 1, а на выходе, помимо суммы, также равный 0 или 1 перенос в следующий разряд.
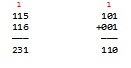
Рис. 7.1. Сложение трёхразрядных чисел "в столбик" с переносом (перенос выделен красным) в десятичной (слева) и двоичной (справа) системах исчисления.
Очевидно, что для двоичной системы (речь об одном разряде) не только перенос, но и слагаемые, и сумма представлены одним битом (одной двоичной цифрой). Поскольку мы вольны интерпретировать значение 0/1 и как целое число, и как ложь/истину, то мы можем рассматривать логические схемы как арифметические функции, которые оперируют числами в двоичной записи (то есть представленными при помощи цифр 0 и 1). При одноразрядном сложении мы руководствуемся следующими правилами:
-
s содержит результат суммы двух слагаемых a и b и переноса из предыдущего разряда c по модулю
; -
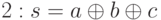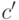содержит значение переноса; перенос возникает при сложении двух одноразрядных двоичных чисел, когда их сумма плюс значение переноса из предыдущего разряда превышает 
.
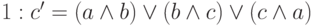Итак, мы имеем функцию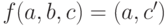 
. Таблица истинности для этой функции представлен в таблице 7.1. Очевидно, что так заданный одноразрядный сумматор является одним шагом для сложения многоразрядных двоичных чисел.
| a | b | c | s | c ' |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
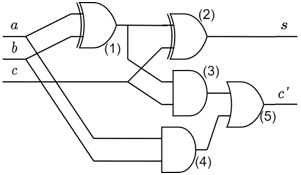
Реализация одноразрядного сумматора с помощью вентилей, то есть логическая схема сумматора, представлена на рис. 1.5. Убедимся, что эта схема действительно делает то, что нужно, то есть соответствует таблице 7.1.
- Разряд суммы s. Входы a и b схемы поступают на вход вентиля (1) "исключающее или", а его выход и вход c, в свою очередь, на вход вентиля (2) "исключающее или". Выход же вентиля (2) является одновременно и выходом схемы c. Таким образом, получаем, что
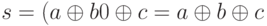, то есть на выходе s мы действительно имеем разряд суммы. - Перенос в следующий разряд
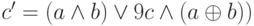. Эта формула отличается от ранее предложенной для 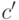, но легко убедиться, что она даёт тот же результат, причём с использованием меньшего количества вентилей. Действительно, 
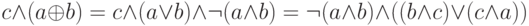, следовательно, 
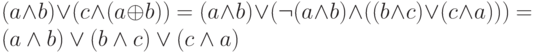, то есть мы получаем именно то, что нам и требовалось.
ЧЕТЫРЕХРАЗРЯДНЫЙ ДВОИЧНЫЙ СУММАТОР
Теперь, когда мы умеем складывать одноразрядные числа, перейдём к сложению двоичных многоразрядных чисел. Без потери общности рассмотрим сложение 4-разрядных чисел.
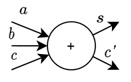
Снова вспомним сложение "в столбик" многоразрядных чисел. Обратим внимание, что оно "сконструировано" из множества одноразрядных сложений с переносом. Если принять во внимание, что система исчисления у нас двоичная, и логическая схема сложения одноразрядных чисел у нас уже есть, то можно сконструировать из набора одноразрядных сумматоров многоразрядный. Для удобства обозначим уже построенный нами одноразрядный сумматор так, как показано на рис.7.3.
4-разрядный сумматор, складывающий числа, состоящие из цифр 
и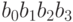 
соответственно (младшие разряды мы записали слева), можно представить, как функцию следующего вида:
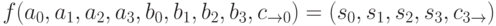
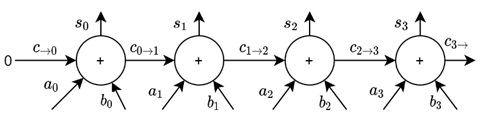
Логическая схема для этой функции показана на рис.7.4. Как и положено, каждый из четырёх одноразрядных сумматоров на этой схеме получает два бита исходных слагаемых и бит переноса из предыдущего разряда, а выдаёт бит суммы и бит переноса в следующий разряд.
Внимательные читатели могли заметить вход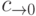 
, на который подаётся 0, и выход 
. Они оставлены на схеме не только для поддержания надлежащей степени общности. При помощи них можно объединять четырёхразрядные сумматоры в более "длинные", подсоединяя выход переноса предыдущего ко входу переноса следующего так же, как мы соединяли одноразрядные сумматоры, получая восьмиразрядные, двенадцать разрядные, шестнадцатиразрядные и так далее. Кроме того, поскольку в современных компьютерах этот вход и выход доступны для программ (при помощи так называемого флага переноса), то пользуясь ими, можно программно реализовать длинную арифметику, то есть запрограммировать функции, которые на компьютере с 64-битной арифметикой смогут выполнять операции над целыми числами произвольной длины.
Оптимизация сумматора с целью ускорения переноса
Современные компьютеры оперируют как правило 32-х или 64-х битными целыми числами. При этом при сложении таких чисел узким местом является перенос: сигнал переноса должен быть последовательно обработан во всех разрядах двоичного представления числа, начиная с младшего и заканчивая старшим. Последовательное выполнение переноса является причиной существенного замедления работы сумматоров. Для ускорения переноса при проектировании современных сумматоров используется специальный приём распараллеливания, который мы рассмотрим на примере 64-битного сумматора.
