Двоичная система исчисления и машинная арифметика

Соответственно, минимально допустимое восьмибитовое целое число будет равно -255. Отметим, что представленный способ представления целых числе называется прямым представлением. Его недостатком является необходимость обрабатывать знаковый разряд специальным образом, отличным от того, как обрабатываются остальные разряды восьмибитового целого числа. Для того, чтобы решить эту проблему, введём понятие дополнительного представления целого числа.

Дополнительное представление неотрицательного числа (то есть числа, старший разряд которого равен 0) тождественно прямому представлению. Если же мы имеем двоичное отрицательное число, то сначала мы инвертируем все двоичные разряды этого числа (то есть вместо 1 записываем 0, вместо 0 записываем 1). Знаковый разряд мы оставляем неизменным. После этого мы прибавляем к модулю данного числа единицу. Если мы получаем переполнение в предпоследнем старшем разряде, то единицу переносы мы отбрасываем.

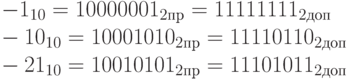
Теперь мы получаем следующее преимущество при выполнении операции вычитания по сравнению с использованием прямого представления: . То есть мы заменяем операцию вычитания сложением с отрицательным вычитаемым (из школьного курса математики мы можем помнить, что первый аргумент операции вычитания называется уменьшаемое, а второй - вычитаемым). Ниже представлен пример.

Единицы измерения цифровых данных

бит принято называть килобитом (Kbit), поскольку 1024 очень близко к 1000 и тут срабатывает аналогия с другими единицами измерения - с километром, в котором 1000 метров, килограммом, в котором 1000 грамм и т.д. Килобиты, точнее, килобиты в секунду (Kbit/s), используются при указании скорости передачи информации, например, для факсимильных аппаратов и модемов^{2Для обозначения числа в 1998 году Международной электротехнической комиссией была стандартизована бинарная приставка "киби". Аналогично, числу 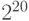соответствует "меби-", а не "мега-", 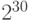- "гиби-", а не "гига-" и т.д. Но десятичные приставки применительно к соответствующим степеням 2 успели "прижиться" раньше появления двоичных, поэтому именно они повсеместно используются до сих пор.}.

байт принято называть килобайтом (Kb). Не так давно в килобайтах измеряли различные виды памяти ЭВМ: оперативную память, постоянное запоминающее устройство, видеопамять и т.д. Сейчас для этих целей применяются более крупные единицы (см. ниже).

байт равно примерно одному миллиону байт и составляет один мегабайт (Mb).

байт равно примерно одному миллиарду байт и составляет один гигабайт (Gb). Несколько гигабайт составляют объём оперативной памяти современного типового персонального компьютера, несколько десятков гигабайт - объем современного флэш-накопителя (флэшки). Такие объёмы появились в обиходе в связи с активным использованием видеоданных и появлением высокоскоростного Интернета. Приведём следующий интересный факт о гигабайтах и флэш-накопителях. Файловая система FAT-32, используемая сегодня на многих небольших флэш-накопителях, не поддерживает работу с файлами размером более 4 гигабайт. Соответственно, возникают проблемы при копировании файлов с видео в высоком качестве на такие флэш-накопители (часто размер таких файлов превышает 4 гигабайта). При необходимости работы с крупными файлами следует использовать другие файловые системы (например, NTFS или exFAT).

байт равно одному триллиону байт и составляет один терабайт (Tb). Типичный объём жесткого диска современного настольного компьютера составляет 0,5-2 терабайта.

байт - один петабайт (Pb). Нетрудно посчитать, что это составляет 1024 терабайт. Данными, измеряемыми в этих единицах, оперируют уже не отдельные люди, а крупные организации и датацентры. Петабайт - действительно крупная единица: для примера, один петабайт составляет непрерывная видеозапись хорошего качества длительностью около полутора месяцев. Но в отдельных случаях и такие объёмы оказываются слишком малы. Так, датчики Большого Адронного Коллайдера во время экспериментов могут генерировать до петабайта данных ежесекундно. На жёстких дисках подобное количество данных хранить уже слишком дорого, поэтому для этого часто используются менее удобные в обращении, но гораздо более дешёвые и ёмкие магнитные ленты.

Вопросы

1. Почему двоичная система исчисления является базовой для представления данных в ЭВМ?
2. Чем число отличается от цифры?
3. Составьте алгоритм перевода десятичной записи числа в двоичную.
4. Обобщите этот алгоритм до произвольной k-ичной системы исчисления.
5. Докажите единственность k-ичного представления любого натурального числа.
6. Дайте определения бита.
7. Дайте определение байта.
8. Дайте определение машинного слова. Приведите примеры длины машинного слова для разных процессоров.
9. Какие характеристики ЭВМ определяет машинное слово?
10. Опишите прямое машинное представление целого числа.
11. Каков недостаток прямого представления целого числа?
12. Каким будет максимально возможное значение шестнадцатибитового целого числа в случае, если отрицательные числа нас не интересуют?
13. Какими будут максимально и минимально возможные целые шестнадцатибитовые числа?
14. Что такое знаковый разряд?
15. Опишите алгоритм построение дополнительного кода для целого числа.
16. Приведите примеры вычитания двух двоичных чисел на основе дополнительного кода.
17. Каким множителям при обозначении количества данных соответствуют приставки кило-, мега-, гига- и тера-?

Литература

1. Харрис Д.М., Харрис С.Л. Цифровая схемотехника и архитектура компьютера. [пер. с англ.] Imagination Technologies. М.: ДМК Пресс, 2018. 792 с.