|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Современные симметричные алгоритмы шифрования
7.6 Алгоритм "Кузнечик"
См. ([3])
Структура шифра "Кузнечик" является вариантом подстановочно-перестановочной сети (SP-сети). Каждый раунд состоит из наложения ключа с помощью операции побитового XOR, нелинейной подстановки (S-блоков замен) и линейного перемешивания.
За счет преобразования всего блока данных на каждом шаге обеспечивается гораздо более быстрое перемешивание входных данных по сравнению со схемой Фейстеля. Кроме того, слой линейного преобразования конструируется таким образом, чтобы обеспечить максимально возможное рассеивание. Для этих целей используется так называемая MDS матрица --- используемая в качестве линейного преобразования  матрица над конечным полем
матрица над конечным полем  , такая, что любые два вектора вида
, такая, что любые два вектора вида  имеют как минимум
имеют как минимум 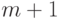 различающихся компонент. То есть набор векторов вида
различающихся компонент. То есть набор векторов вида 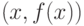 обладает свойством максимальной разнесенности (maximum distance separable). Поэтому адекватная стойкость таких алгоритмов достигается за меньшее, по сравнению со схемой Фейстеля, число раундов.
обладает свойством максимальной разнесенности (maximum distance separable). Поэтому адекватная стойкость таких алгоритмов достигается за меньшее, по сравнению со схемой Фейстеля, число раундов.
Как и в алгоритме AES, линейное преобразование алгоритма "Кузнечик" использует операции с байтами, представляя их как элементы поля Галуа  . В "Кузнечике" оно построенного с помощью неприводимого полинома
. В "Кузнечике" оно построенного с помощью неприводимого полинома 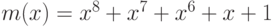 . SP-сети с линейным преобразованием, состоящим из двух частей, первая из которых похожа на операцию MixColumns, а вторая --- на операцию ShiftRows алгоритма AES, называют AES-подобными (like AES).
. SP-сети с линейным преобразованием, состоящим из двух частей, первая из которых похожа на операцию MixColumns, а вторая --- на операцию ShiftRows алгоритма AES, называют AES-подобными (like AES).
Байты-константы нам будет удобно зававать целыми числами, двоичные разряды которых есть соответствующие коэффициенты полинома. Например, под числом  мы будем понимать байт
мы будем понимать байт  .
.
Шифр "Кузнечик" имеет размер входного блока данных 128 бит, длину ключа 256 бит и выполняет 10 раундов шифрования. В последнем раунде выполняется только одна операция --- наложения раундового ключа.
Первой выполняется операция наложения ключа раунда с помощью побитового XOR:  = k\oplus a](/sites/default/files/tex_cache/110e9a61f75058e443cf0203592631ed.png) .
.
Затем входной 128-битовый блок  алгоритма шифрования представляется в виде последовательности 16 байтов, которые нумеруются справа налево, начиная с 0:
алгоритма шифрования представляется в виде последовательности 16 байтов, которые нумеруются справа налево, начиная с 0: 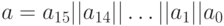 , где знаком
, где знаком 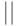 обозначена операция конкатенации строк.
обозначена операция конкатенации строк.
К каждому байту применяется нелинейная подстановка, задаваемая массивом
 = (252, 238, 221, 17, 207, 110, 49, 22, 251, 196, 250, 218, 35, 197, 4, 77, 233, 119, 240, 219, 147, 46, 153, 186, 23, 54, 241. 187, 20, 205, 95, 193, 249, 24, 101, 90, 226, 92, 239, 33, 129, 28, 60, 66, 139, 1, 142, 79, 5, 132, 2, 174, 227, 106, 143, 160, 6, 11, 237, 152, 127, 212, 211, 31, 235, 52, 44, 81, 234, 200, 72, 171, 242, 42, 104, 162, 253, 58, 206, 204, 181, 112, 14, 86, 8, 12, 118, 18, 191, 114, 19, 71, 156, 183, 93, 135, 21, 161, 150, 41, 16, 123, 154, 199, 243, 145, 120, 111, 157, 158, 178, 177, 50, 117, 25, 61, 255, 53, 138, 126, 109, 84, 198, 128, 195, 189, 13, 87, 223, 245, 36, 169, 62, 168, 67, 201, 215, 121, 214, 246, 124, 34, 185, 3, 224, 15, 236, 222, 122, 148, 176, 188, 220, 232, 40, 80, 78, 51, 10, 74, 167, 151, 96, 115, 30, 0, 98, 68, 26, 184, 56, 130, 100, 159, 38, 65, 173, 69, 70, 146, 39, 94, 85, 47, 140, 163, 165, 125, 105, 213, 149, 59, 7, 88, 179, 64, 134, 172, 29, 247, 48, 55, 107,
228, 136, 217, 231, 137, 225, 27, 131, 73, 76, 63, 248, 254, 141, 83, 170, 144, 202, 216, 133, 97, 32, 113, 103, 164, 45, 43, 9, 91, 203, 155, 37, 208, 190, 229, 108, 82, 89, 166, 116, 210, 230, 244, 180, 192, 209, 102, 175, 194, 57, 75, 99, 182).
= (252, 238, 221, 17, 207, 110, 49, 22, 251, 196, 250, 218, 35, 197, 4, 77, 233, 119, 240, 219, 147, 46, 153, 186, 23, 54, 241. 187, 20, 205, 95, 193, 249, 24, 101, 90, 226, 92, 239, 33, 129, 28, 60, 66, 139, 1, 142, 79, 5, 132, 2, 174, 227, 106, 143, 160, 6, 11, 237, 152, 127, 212, 211, 31, 235, 52, 44, 81, 234, 200, 72, 171, 242, 42, 104, 162, 253, 58, 206, 204, 181, 112, 14, 86, 8, 12, 118, 18, 191, 114, 19, 71, 156, 183, 93, 135, 21, 161, 150, 41, 16, 123, 154, 199, 243, 145, 120, 111, 157, 158, 178, 177, 50, 117, 25, 61, 255, 53, 138, 126, 109, 84, 198, 128, 195, 189, 13, 87, 223, 245, 36, 169, 62, 168, 67, 201, 215, 121, 214, 246, 124, 34, 185, 3, 224, 15, 236, 222, 122, 148, 176, 188, 220, 232, 40, 80, 78, 51, 10, 74, 167, 151, 96, 115, 30, 0, 98, 68, 26, 184, 56, 130, 100, 159, 38, 65, 173, 69, 70, 146, 39, 94, 85, 47, 140, 163, 165, 125, 105, 213, 149, 59, 7, 88, 179, 64, 134, 172, 29, 247, 48, 55, 107,
228, 136, 217, 231, 137, 225, 27, 131, 73, 76, 63, 248, 254, 141, 83, 170, 144, 202, 216, 133, 97, 32, 113, 103, 164, 45, 43, 9, 91, 203, 155, 37, 208, 190, 229, 108, 82, 89, 166, 116, 210, 230, 244, 180, 192, 209, 102, 175, 194, 57, 75, 99, 182).
Поскольку каждый байт  может принимать значение от 0 до 255, массив
может принимать значение от 0 до 255, массив  имеет 256 элементов. Это значит, что при
имеет 256 элементов. Это значит, что при  значение
значение  будет заменено на
будет заменено на 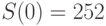 , при
, при 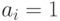 --- на
--- на 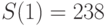 , и так далее (все числа записаны в десятеричном виде). Для выходного блока в целом нелинейная подстановка может быть определена как
, и так далее (все числа записаны в десятеричном виде). Для выходного блока в целом нелинейная подстановка может быть определена как
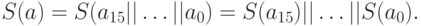
Линейное перемешивание  шифра "Кузнечик" может быть описано с помощью линейного регистра сдвига
шифра "Кузнечик" может быть описано с помощью линейного регистра сдвига  :
:
- Байты
 представляются в виде полиномов из поля Галуа
представляются в виде полиномов из поля Галуа  . Для простоты будем их также обозначать
. Для простоты будем их также обозначать  .
. - В поле
 вычисляется байт
вычисляется байт  .
. - Записываем
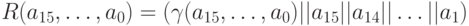 .
. - Шаги 1-3 повторяются 16 раз; при этом получаемая строка
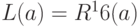 не содержит ни одного не преобразованного символа.
не содержит ни одного не преобразованного символа.
Шифрование 128-битного входного блока  описывается следующей формулой:
описывается следующей формулой:
![E(a) = X[K_{10}LSX[K_9]LSX[K_8]\ldots LSX[K_1](a).](/sites/default/files/tex_cache/dc09fb91246bef9f2e00f0cf4a3d7d14.png)
Здесь 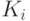 --- раундовые ключи, записанные подряд преобразования
--- раундовые ключи, записанные подряд преобразования ![LSX[K_i]](/sites/default/files/tex_cache/6ec0c9f0bda545a0884a2bb2f6e1fb96.png) обозначают последовательное применение преобразований справа налево. То есть, сначала выполняется прибавление ключа, затем нелинейная подстановка
обозначают последовательное применение преобразований справа налево. То есть, сначала выполняется прибавление ключа, затем нелинейная подстановка  , затем линейное перемешивание
, затем линейное перемешивание  .
.
