|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгебраические системы
3.1.5 Конечные кольца и поля
Определение 3.18 Множество  с двумя алгебраическими операциями
с двумя алгебраическими операциями 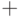 ,
,  называется ассоциативным кольцом, если в нём выполняются свойства:
называется ассоциативным кольцом, если в нём выполняются свойства:
 является коммутативной группой по сложению с нейтральным элементом
является коммутативной группой по сложению с нейтральным элементом  (эта группа называется аддитивной).
(эта группа называется аддитивной). является полугруппой (обозначается
является полугруппой (обозначается 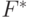 ).
).- Дистрибутивность:
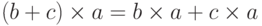 и
и  .
.
Определение 3.19 Кольца  и
и  называются изоморфными, если существует отображение
называются изоморфными, если существует отображение  , являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
, являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
Определение 3.20 Полем называется кольцо  , в котором
, в котором 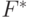 является коммутативной группой.
является коммутативной группой.
Определение 3.21 Характеристикой поля называется наименьшее такое натуральное число  , что
, что 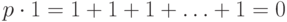 , или 0, если такого
, или 0, если такого  не существует. Характеристика поля может быть только простым числом или нулем.
не существует. Характеристика поля может быть только простым числом или нулем.
Определение 3.22 Левым (правым) идеалом кольца называется любое его подкольцо, выдерживающее умножение слева (соответственно, справа) на любой элемент кольца. Подкольцо, являющееся левым и правым идеалом, называется двусторонним идеалом, или просто идеалом.
Подкольцо  разбивает кольцо
разбивает кольцо  на классы эквивалентности:
на классы эквивалентности: 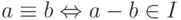 . Класс, содержащий элемент
. Класс, содержащий элемент  , можно записать в виде:
, можно записать в виде:

Если подкольцо является идеалом, то на множестве таких классов можно ввести операции сложения и умножения, относительно которых множество классов образует кольцо, называемое фактор-кольцом:
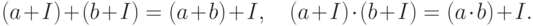
Из определения идеала следует, что результат операций не зависит от выбора представителей  ,
,  , то есть операции заданы корректно.
, то есть операции заданы корректно.
Наиболее важными для нас будут следующие кольца и поля:
- Кольцо целых чисел
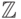 относительно обыкновенных операций сложения и умножения.
относительно обыкновенных операций сложения и умножения. - Поле рациональных чисел
 относительно операций сложения и умножения.
относительно операций сложения и умножения. - Фактор-кольцо
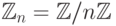 кольца целых чисел по идеалу всех чисел, кратных
кольца целых чисел по идеалу всех чисел, кратных  . Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших
. Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших  , с операцией сложения и умножения по модулю
, с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда
. Такое кольцо является полем тогда и только тогда, когда  - простое число.
- простое число. - Кольцо
![F[{x_1,{\dots}, x_n}]](/sites/default/files/tex_cache/5830bd1f7c4224bdde9427103672e170.png) многочленов от переменных
многочленов от переменных 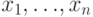 над произвольным полем
над произвольным полем  .
. - Фактор-кольцо
![F[{x}] / f(x) F[x]](/sites/default/files/tex_cache/00d09f4ebf7f7e40fc59b3267bf73e48.png) кольца многочленов над полем
кольца многочленов над полем  по идеалу, порожденному одним многочленом
по идеалу, порожденному одним многочленом 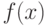 степени
степени  , то есть состоящему из всех многочленов, кратных
, то есть состоящему из всех многочленов, кратных  . Это кольцо можно также рассматривать, как кольцо многочленов степени меньше
. Это кольцо можно также рассматривать, как кольцо многочленов степени меньше  с операцией сложения и умножения по модулю
с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда многочлен
. Такое кольцо является полем тогда и только тогда, когда многочлен  неприводим над
неприводим над  .
.
В криптографии нас будут интересовать больше всего конечные поля, то есть поля с конечным множеством  . Перечислим наиболее важные для нас свойства:
. Перечислим наиболее важные для нас свойства:
- Каждое конечное поле имеет простую характеристику
 .
. - Поле простого порядка не имеет подполей, и называется простым.
- Конечное поле характеристики
 содержит подполе порядка
содержит подполе порядка  .
. - Конечное поле является линейным пространством над своим простым подполем, поэтому имеет порядок
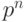 для некоторого натурального числа
для некоторого натурального числа  .
. - Мультипликативная группа конечного поля циклическая. Если поле имеет простой порядок
 , то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю
, то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю  .
. - Конечные поля одного порядка изоморфны.
Рассмотрим несколько связанных с кольцами вычетов задач, часто возникающих в криптографии.
Пример 3.5 Найти мультипликативный порядок элемента 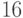 по модулю
по модулю  , то есть порядок элемента
, то есть порядок элемента 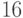 мультипликативной группы
мультипликативной группы  .
.
Решение. Поскольку число 101 простое, порядок мультипликативной группы поля  равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
После того, как обнаружили, что 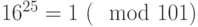 , возводить в
, возводить в 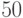 -ю и
-ю и 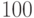 -ю степень излишне - видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
-ю степень излишне - видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
Пример 3.6 Найти случайный примитивный корень по модулю  .
.
Решение. Порядок мультипликативной группы поля вычетов по модулю 883 равен 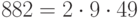 . Будем выбирать случайное число
. Будем выбирать случайное число  и возводить его в степени
и возводить его в степени  ,
,  ,
,  . Если в какой-то степени
. Если в какой-то степени  даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел
даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел  ,
,  ,
,  , то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы
, то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы  , а в следующих колонках - результаты возведения в степень.
, а в следующих колонках - результаты возведения в степень.
Итак, 326 является примитивным корнем по модулю 883.




