|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгебраические системы
3.1.3 Коммутативные и ассоциативные операции
Определение 3.5 Бинарная операция  на множестве
на множестве  называется ассоциативной, если
называется ассоциативной, если  для всех
для всех 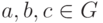 .
.
Определение 3.6 Бинарная операция  на множестве
на множестве  называется коммутативной, если
называется коммутативной, если  для всех
для всех  .
.
Свойства ассоциативности и коммутативности независимы. Действительно, например операция на 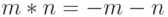 на
на 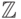 является коммутативной, но не ассоциативной, а операция умножения квадратных
является коммутативной, но не ассоциативной, а операция умножения квадратных  -матриц - ассоциативна, но не коммутативна.
-матриц - ассоциативна, но не коммутативна.
Пример 3.2
- Операции сложения и умножения на множестве
 действительных чисел коммутативны и ассоциативны.
действительных чисел коммутативны и ассоциативны. - Операция
 на множестве натуральных чисел, задаваемая формулой
на множестве натуральных чисел, задаваемая формулой 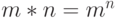 - некоммутативна (например,
- некоммутативна (например, 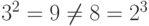 ). Эта операция и неассоциативна (упражнение: приведите пример трех чисел
). Эта операция и неассоциативна (упражнение: приведите пример трех чисел  таких, что
таких, что 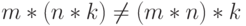 .
. - Операция на множестве
 , заданная формулой
, заданная формулой 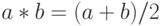 - коммутативна, но не ассоциативна.
- коммутативна, но не ассоциативна.
3.1.4 Группы и полугруппы
Определение 3.7 Множество  с определённой на нём ассоциативной бинарной операцией
с определённой на нём ассоциативной бинарной операцией  называется полугруппой. Полугруппа, в которой есть нейтральный элемент, называется моноидом.
называется полугруппой. Полугруппа, в которой есть нейтральный элемент, называется моноидом.
Примеры полугрупп.
-
 - полугруппа без нейтрального элемента.
- полугруппа без нейтрального элемента.
 - моноид.
- моноид. -
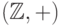 - моноид.
- моноид. -
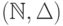 , где
, где  ,
,
 , где
, где  .
. -
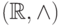 , где
, где  ,
,
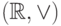 , где
, где  .
.
Пусть  - произвольное (непустое) множество. Зададимся вопросом: можно ли превратить
- произвольное (непустое) множество. Зададимся вопросом: можно ли превратить  в полугруппу? Другими словами, можно ли задать на
в полугруппу? Другими словами, можно ли задать на  какую-нибудь ассоциативную операцию? Ответ утвердительный. Более того, если
какую-нибудь ассоциативную операцию? Ответ утвердительный. Более того, если  неодноэлементно, то это можно сделать многими способами, а при бесконечном
неодноэлементно, то это можно сделать многими способами, а при бесконечном  - бесконечным числом способов. Укажем несколько таких способов.
- бесконечным числом способов. Укажем несколько таких способов.
- Положим
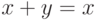 для любых
для любых  . Очевидно, введенная операция
. Очевидно, введенная операция 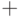 ассоциативна. Полугруппу с такой операцией называют полугруппой левых нулей.
ассоциативна. Полугруппу с такой операцией называют полугруппой левых нулей. - Положим
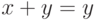 для любых
для любых  . Этот пример полугруппы правых нулей аналогичен предыдущему.
. Этот пример полугруппы правых нулей аналогичен предыдущему. - Зафиксируем элемент
 и положим
и положим  для любых
для любых  . И эта операция
. И эта операция 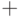 , очевидно, ассоциативна.
, очевидно, ассоциативна.
Свободные полугруппы
Пусть  - произвольное (непустое) множество. Будем называть
- произвольное (непустое) множество. Будем называть  алфавитом, а элементы
алфавитом, а элементы  - буквами. Через
- буквами. Через  обозначим множество всех конечных последовательностей букв из
обозначим множество всех конечных последовательностей букв из  . Зададим на
. Зададим на  операцию умножения, полагая
операцию умножения, полагая 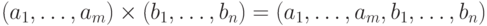 . Легко видеть, что эта операция (называемая иногда конкатенацией, то есть сцеплением) ассоциативна (упражнение: проверить), так что
. Легко видеть, что эта операция (называемая иногда конкатенацией, то есть сцеплением) ассоциативна (упражнение: проверить), так что  становится полугруппой, которая называется свободной полугруппой над алфавитом
становится полугруппой, которая называется свободной полугруппой над алфавитом  . Другое употребительное обозначение для нее :
. Другое употребительное обозначение для нее : 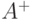 . Отождествляя последовательность из одной буквы с самой этой буквой и опуская в записи знак для конкатенации, элементы свободной полугруппы записывают в виде
. Отождествляя последовательность из одной буквы с самой этой буквой и опуская в записи знак для конкатенации, элементы свободной полугруппы записывают в виде 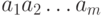 и называют словами.
По определению, слова
и называют словами.
По определению, слова 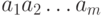 и
и 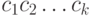 равны, если
равны, если  и
и  при
при 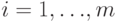 .
.
Свободные полугруппы играют важную роль как в общей теории полугрупп, так и в приложениях. Их прикладная роль объясняется, в частности, тем, что во многих процессах передачи информации передаваемые сообщения представляют собой цепочки символов ("реальных" букв или слов, других кодовых знаков, электрических сигналов и т.д.) и соединение двух таких цепочек есть не что иное, как конкатенация слов в подходящей свободной полугруппе. Свободные полугруппы (главным образом, над конечными алфавитами) являются исходным объектом в теории формальных языков и теории кодов, существенна их роль в теории автоматов. При этом обычно к элементам полугруппы  добавляют так называемое пустое слово, не содержащее букв и играющее роль единицы при умножении, получается полугруппа с единицей, обозначаемая
добавляют так называемое пустое слово, не содержащее букв и играющее роль единицы при умножении, получается полугруппа с единицей, обозначаемая 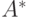 и называемая свободным моноидом над алфавитом
и называемая свободным моноидом над алфавитом  .
.
Формальным языком называется произвольное подмножество некоторого свободного моноида.
Определение 3.8 Полугруппа с единицей, в которой для каждого элемента существует обратный, называется группой.
Определение 3.9 Если операция в группе  обладает коммутативностью, т.е.
обладает коммутативностью, т.е.
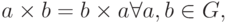
то группа  называется коммутативной.
называется коммутативной.
Определение 3.10 Мощность множества  , на котором задана групповая операция, называется порядком группы
, на котором задана групповая операция, называется порядком группы  .
.
Если множество конечно, то группа  называется конечной.
называется конечной.
Определение 3.11 Подмножество множества  , являющееся одновременно группой относительно той же самой операции, называется подгруппой группы
, являющееся одновременно группой относительно той же самой операции, называется подгруппой группы  .
.
Определение 3.11 Подгруппа  группы
группы  называется тривиальной, если либо
называется тривиальной, если либо  , либо
, либо  состоит из одного нейтрального элемента.
состоит из одного нейтрального элемента.
Справедлива
Теорема 3.1 (Теорема Лагранжа) Порядок  конечной группы
конечной группы  делится на порядок
делится на порядок  любой её подгруппы
любой её подгруппы  .
.
Определение 3.12 Число 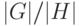 называется индексом подгруппы
называется индексом подгруппы  в группе
в группе  и обозначается
и обозначается 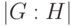 .
.
Определение 3.13 Полугруппы  и
и  называются изоморфными, если существует взаимно однозначное отображение
называются изоморфными, если существует взаимно однозначное отображение 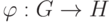 , сохраняющее операцию, то есть такое, что
, сохраняющее операцию, то есть такое, что 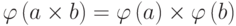 .
.
Определение 3.14 Подгруппа группы  называется максимальной, если она не содержится в других собственных (не совпадающих с
называется максимальной, если она не содержится в других собственных (не совпадающих с  ) подгруппах группы
) подгруппах группы  .
.
Определение 3.15 Минимальная подгруппа группы  , содержащая элементы
, содержащая элементы 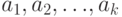 , называется подгруппой, порождённой этими элементами, и обозначается
, называется подгруппой, порождённой этими элементами, и обозначается 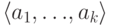 .
.
Определение 3.16 Группа 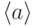 , порождённая одним элементом, называется циклической, и состоит из элементов
, порождённая одним элементом, называется циклической, и состоит из элементов 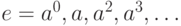 .
.
Существуют две возможности: либо все степени элемента  различны, тогда список элементов группы
различны, тогда список элементов группы 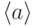 будет продолжаться бесконечно, либо на каком-то шаге окажется:
будет продолжаться бесконечно, либо на каком-то шаге окажется:  .
.
Определение 3.17 Минимальное натуральне число  такое, что
такое, что 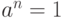 , называется порядком элемента
, называется порядком элемента  (пишут
(пишут 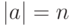 ). Если такого
). Если такого  не существует, пишут
не существует, пишут  .
.
Одновременно такое  является порядком подгруппы
является порядком подгруппы 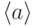 .
.
Справедливо
Следствие 3.1 (из теоремы Лагранжа) Порядок конечной группы  делится на порядок любого её элемента.
делится на порядок любого её элемента.
Отметим несколько свойств циклической группы, которые пригодятся нам в дальнейшем:
- Каждая подгруппа циклической группы циклическая.
- Если порядок элемента
 равен
равен  , то порядок элемента
, то порядок элемента 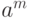 равен
равен  .
. - Если
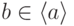 имеет порядок
имеет порядок 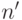 , то
, то  лежит в подгруппе
лежит в подгруппе  .
. - Если
 делит
делит  , то
, то 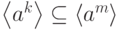 .
. - Максимальными в циклической группе
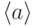 порядка
порядка  являются подгруппы
являются подгруппы 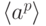 для простых чисел
для простых чисел  , делящих
, делящих  , и только они.
, и только они. - Если в группе
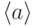 найдётся элемент
найдётся элемент  порядка
порядка  , то группа
, то группа 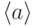 порождается и элементом
порождается и элементом  , то есть
, то есть  .
. - Число элементов, порождающих
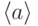 , равно
, равно 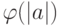 .
. - Циклические группы одного порядка изоморфны.
Пример 3.3 Множество 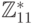 чисел от
чисел от  до
до  c умножением по модулю
c умножением по модулю  образует группу. Отметим, что в этой группе нейтральным элементом является
образует группу. Отметим, что в этой группе нейтральным элементом является  , элемент
, элемент  имеет порядок
имеет порядок  , поскольку
, поскольку  , элементы
, элементы 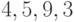 имеют порядок
имеют порядок 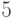 , а остальные элементы имеют порядок, не делящий ни
, а остальные элементы имеют порядок, не делящий ни  , ни
, ни 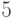 , но делящий
, но делящий  . То есть элементы
. То есть элементы 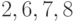 имеют порядок
имеют порядок  , то есть
, то есть  .
.
Пример 3.4 Пусть элемент  группы
группы  имеет порядок
имеет порядок  . Найти число
. Найти число  элементов порядка
элементов порядка 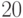 в группе
в группе 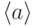 ? Сколько элементов являются порождающими в
? Сколько элементов являются порождающими в 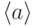 ?
?
Решение. По свойству 2, элементы порядка 20 лежат в подгруппе 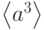 и, по свойствам 3,5, не лежат в её максимальных подгруппах:
и, по свойствам 3,5, не лежат в её максимальных подгруппах: 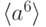 и
и 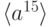 . Отсюда,
. Отсюда,
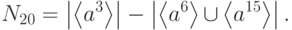
Порядок элементов из  делит и 10 и 4, следовательно, равен 1 или 2, т.е.
делит и 10 и 4, следовательно, равен 1 или 2, т.е. 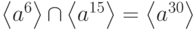 ,
, 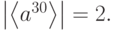 Отсюда,
Отсюда,
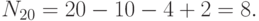
Число  порождающих элементов в
порождающих элементов в 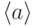 , то есть элементов порядка 60, можно найти по формуле:
, то есть элементов порядка 60, можно найти по формуле:
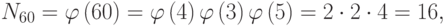
где  - функция Эйлера.
- функция Эйлера.
