НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 1: Основы теории чисел

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2785 / 698 | Длительность: 21:50:00

Специальности: Программист, Администратор информационных систем, Специалист по безопасности, Архитектор программного обеспечения, Разработчик интернет-проектов

|

Вам нравится? Нравится 57 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.2.5 Сравнения первой степени

Любое сравнение первой степени с одним неизвестным можно привести к виду

$ax \equiv b~(mod \ m),$

( 1.4)

где $a \not\equiv 0 ~(mod \ m)$ .

Выясним условия, при которых сравнение (1.4) имеет:

единственное решение,
несколько решений,
не имеет решений.

Теорема 1.17 Для того, чтобы сравнение (1.4) имело хотя бы одно решение, необходимо и достаточно, чтобы число делилось на .

Пример 1.24 Сравнение 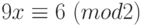$9x\equiv 6~(mod \12)$ имеет решение, так как делится на .

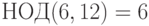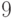Пример 1.25 Сравнение $6x\equiv 9 ~(mod \12)$ не имеет решений, так как , а не делится на .

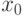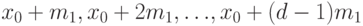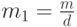Теорема 1.18 Пусть сравнение (1.4) разрешимо и . Тогда множество решений сравнения (1.4) состоит из классов по модулю , а именно, если ${x}_{0}$ - одно из решений, то все другие решения - это ${x}_{0}+m_1, {x}_{0}+2m_1,{\dots}, {x}_{0}+(d-1)m_1$ , где $m_1= \frac{m}{d}$ .

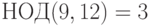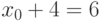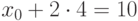Пример 1.26 Сравнение $9x\equiv 6~(mod \ 12)$ имеет ровно три решения, так как . Эти решения: ${x}_{0}=2$ , ${x}_{0}+4=6$ , ${x}_{0}+2 \cdot 4=10$ .

Пример 1.27 Сравнение 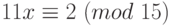$11x\equiv 2~(mod \ 15)$ имеет единственное решение 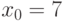${x}_{0}=7$ , т.к. .

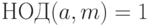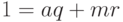Покажем, как решать сравнение первой степени. Рассмотрим случай НОД(a,m)=1 . Тогда решение сравнения (1.4) можно искать, например, по алгоритму Евклида. Действительно, используя расширенный алгоритм Евклида, представим число 1 в виде линейной комбинации чисел и : 1=aq+mr .

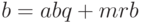Умножим обе части этого равенства на , получим: b=abq+mrb , откуда abq-b=-mrb , то есть $a \cdot (bq) \equiv b~(mod \ m)$ и - решение сравнения (1.4).

Другой способ: использовать теорему Эйлера. Пусть, снова, 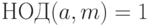НОД(a,m)=1 . Применяем теорему Эйлера: 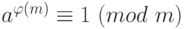${a}^{\varphi (m)}\equiv 1~(mod \ m)$ . Умножим обе части сравнения на : 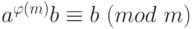${a}^{\varphi (m)}b \equiv b~(mod \ m)$ . Переписывая последнее выражение в виде $a( {a}^{\varphi (m)-1}b) \equiv b~(mod \ m)$ , получаем, что ${a}^{\varphi (m)-1}b$ - решение сравнения (1.4).

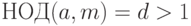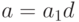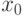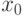Допустим теперь, что НОД(a,m)=d>1 . Тогда a=a_1 d , m=m_1 d , где НОД(a_1,m_1)=1 . Кроме того, необходимо b=b_1 d для того, чтобы сравнение было разрешимо. Если ${x}_{0}$ - решение сравнения $a_1 x\equiv b_1 ~(mod \ m_1)$ , причем единственное, поскольку , то ${x}_{0}$ будет решением и сравнения $a_1 dx\equiv b_1 d ~(mod \ m_1) d$ , то есть исходного сравнения (1.4). Остальные решения (их d-1 ) находим по теореме.

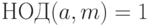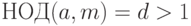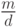Итак, если НОД(a,m)=1 , то сравнение (1.4) имеет единственное решение, и решением сравнения является класс $x=ba^{\varphi(m)-1}~(mod \ m)$ . Если НОД(a,m)=d>1 , не делится на , то сравнение решений не имеет. Если делится на , то сравнение имеет различных решений. Все эти решения образуют один класс по модулю $\frac{m}{d}$ .

Пример 1.28 Решим сравнение: 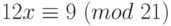$12x\equiv 9~(mod \ 21)$$ .

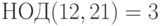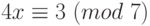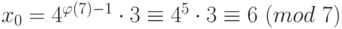Вычисляем НОД(12,21)=3 . Число 9 делится на 3, поэтому сравнение разрешимо, и у него три решения. Поделим обе части сравнения и модуль на их наибольший общий делитель: $4x\equiv 3 ~(mod \ 7)$ . Поскольку НОД(4, 7)=1 , можем воспользоваться теоремой Эйлера: ${x}_{0}={4}^{\varphi \left(7\right)-1} \cdot 3 \equiv {4}^{5} \cdot 3 \equiv 6 ~(mod \ 7)$ .

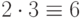Поясним: $\varphi(7)=6$ , $4^{2}=16\equiv 2~(mod \ 7)$ , поэтому ${4}^{5}\equiv 4^{2} \cdot 4^{2} \cdot 4\equiv 2 \cdot 2 \cdot 4\equiv 2$ , и $2 \cdot 3\equiv 6$ .

Таким образом, 6 - это одно из решений сравнения $12x\equiv 9 ~(mod \ 21)$ . Находим остальные решения:

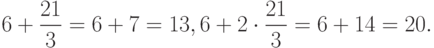
$6+ \frac{21}{3} =6+7=13, 6+2 \cdot \frac{21}{3} =6+14=20.$

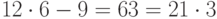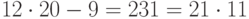Проверка: $12 \cdot 6-9=63=21 \cdot 3$ ; $12 \cdot 13-9=147=21 \cdot 7$ ; $12 \cdot 20-9=231=21 \cdot 11$ .

Пример 1.29 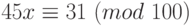$45 x \equiv 31~(mod \ 100)$ .

Так как 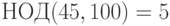НОД(45,100)=5 , а 31 не делится на 5, то решений сравнение 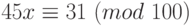$45 x \equiv 31~(mod \ 100)$ не имеет.

Пример 1.30 $51 x \equiv 141~(mod \ 234)$ .

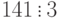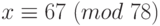Поскольку НОД(51,234)=3 , $141 \, \vdots \, 3$ , то сравнение имеет 3 решения. После деления обеих частей и модуля на 3 получим сравнение: $17 x \equiv 47~(mod \ 78)$ . Решение этого сравнения: $x \equiv 67~(mod \ 78)$ .

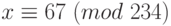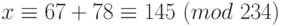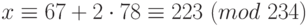Решения исходного сравнения найдём по теореме 1.18: $x \equiv 67~(mod \ 234)$ , $x \equiv 67+78 \equiv 145~(mod \ 234)$ , $x \equiv 67+2\cdot 78 \equiv 223~(mod \ 234)$ .

Дальше >>

Авторизоваться

Криптографические методы защиты информации

Основы теории чисел

1.2.5 Сравнения первой степени

Вопросы и ответы