|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Основы теории чисел
1.2.3 Функция Эйлера. Теоремы Эйлера и Ферма
Определение 1.13 Функция Эйлера  - количество положительных чисел, не превосходящих
- количество положительных чисел, не превосходящих  и взаимно простых с
и взаимно простых с  .
.
Пример 1.13 Пусть  . Взаимно простыми с
. Взаимно простыми с 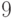 являются числа:
являются числа:  ,
,  ,
, 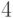 ,
, 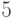 ,
,  ,
,  . Так как количество этих чисел равно
. Так как количество этих чисел равно  , то
, то  .
.
Пример 1.14 Пусть  . Взаимно простые с
. Взаимно простые с  числа, меньшие
числа, меньшие  - это
- это  ,
, ,
, ,
, 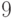 . Поэтому
. Поэтому  .
.
Рассмотрим простое число  . Все числа, меньшие
. Все числа, меньшие  , взаимно просты с ним. Итак,
, взаимно просты с ним. Итак, 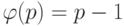 для простого
для простого  .
.
Для чисел 9, 10 можно было вычислить значение функции Эйлера непосредственным перечислением чисел, взаимно простых с данным числом. Для числа 100 сделать это уже труднее, а для 10000 еще труднее. Оказывается, есть формула, позволяющая вычислять значение функции Эйлера достаточно просто.
Пусть задано каноническое разложение числа  :
:
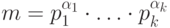 .
.
Тогда 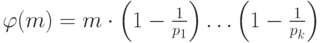 .
.
Пример 1.15
-
Так как
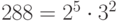 , то
, то  .
. -
Так как
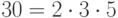 , то
, то 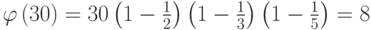 .
. -
Так как
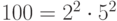 , то
, то 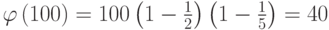 .
.
Теорема 1.15 (Эйлер) Если a - такое число, что 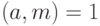 , то
, то 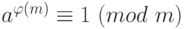 .
.
Пример 1.16 Пусть 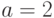 ,
,  . Тогда
. Тогда 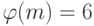 , и по теореме Эйлера получаем:
, и по теореме Эйлера получаем: 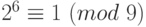 . В справедливости этого равенства легко убедиться, если учесть, что
. В справедливости этого равенства легко убедиться, если учесть, что 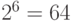 .
.
Пример 1.17 Пусть 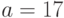 ,
,  . Тогда
. Тогда  , то по теореме Эйлера получаем:
, то по теореме Эйлера получаем: 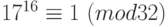 . Убедиться в справедливости этого равенства непосредственным подсчётом было бы затруднительно.
. Убедиться в справедливости этого равенства непосредственным подсчётом было бы затруднительно.
Особенно простой вид теорема Эйлера принимает, если 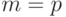 - простое число. В этом случае
- простое число. В этом случае 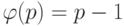 , а потому получаем следующее утверждение:
, а потому получаем следующее утверждение:
Теорема 1.16 (малая теорема Ферма) Если  - простое число и
- простое число и  - целое число, такое, что
- целое число, такое, что 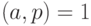 , то
, то 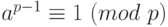 .
.
Часто используется следствие малой теоремы Ферма, если  - простое число, то для любого целого числа a имеет место сравнение:
- простое число, то для любого целого числа a имеет место сравнение: 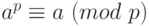 .
.
Рассмотрим примеры на применение теорем Эйлера и Ферма.
Пример 1.18 Найдём остаток отделения 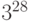 на
на  .
.
Согласно теореме Ферма 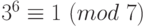 , тогда
, тогда 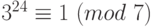 . Кроме того,
. Кроме того, 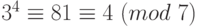 . Тогда
. Тогда 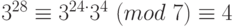 . Следовательно, искомый остаток
. Следовательно, искомый остаток  .
.
Пример 1.19 Найдём остаток от деления 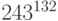 на
на 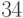 .
.
Имеем: 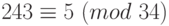 . Тогда
. Тогда  . Согласно теореме Эйлера
. Согласно теореме Эйлера 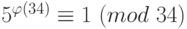 , или
, или 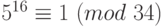 . Далее делим
. Далее делим 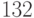 на
на 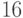 , получим:
, получим:  . Поэтому
. Поэтому  . Таким образом,
. Таким образом, 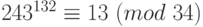 .
.
Следовательно, 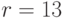 .
.
Пример 1.20 Найдем остаток от деления числа 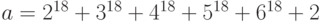 на
на  .
.
Решение. Числа 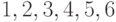 взаимно просты с числом 7. По теореме Ферма,
взаимно просты с числом 7. По теореме Ферма, 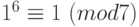 ,
, 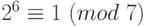 ,
, 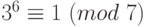 ,
, 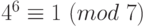 ,
, 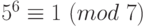 ,
, 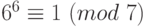 . Возведем эти сравнения в третью степень и сложим, получим:
. Возведем эти сравнения в третью степень и сложим, получим: 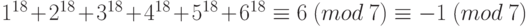 . Следовательно,
. Следовательно,  , то есть число
, то есть число  делится на 7 без остатка.
делится на 7 без остатка.
Пример 1.21 Найти остаток от деления  на
на  .
.
Решение. Число 101 простое, 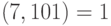 ,
, 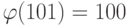 . По теореме Ферма,
. По теореме Ферма, 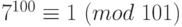 . Возведем это сравнение в четвертую степень, получим:
. Возведем это сравнение в четвертую степень, получим: 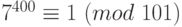 . Умножим полученное сравнение на сравнение
. Умножим полученное сравнение на сравнение 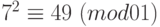 . Итак,
. Итак, 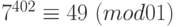 , то есть остаток равен 49.
, то есть остаток равен 49.
Пример 1.22 Доказать, что 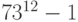 делится на
делится на 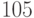 .
.
Решение. Разложим на множители: 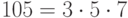 . Далее,
. Далее, 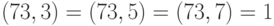 . По теореме Ферма,
. По теореме Ферма, 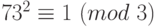 ,
, 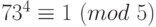 ,
, 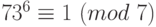 . Возведем первое сравнение в шестую степень, второе в третью степень, третье во вторую, получим:
. Возведем первое сравнение в шестую степень, второе в третью степень, третье во вторую, получим: 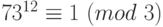 ,
, 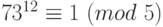 ,
, 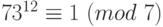 . А отсюда следует, что
. А отсюда следует, что  , так как 105- наименьшее общее кратное чисел 3, 5, 7.
, так как 105- наименьшее общее кратное чисел 3, 5, 7.
Определение 1.14 Число  называется обратным к
называется обратным к  по модулю
по модулю  , если
, если 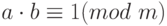 . Пишут:
. Пишут: 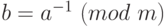 .
.
Например, 3 обратно к 2 по модулю 5, так как 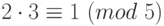 . Заметим, что обратное к
. Заметим, что обратное к  по модулю
по модулю  можно найти лишь в случае
можно найти лишь в случае 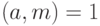 . Если
. Если  , то обратный к
, то обратный к  по модулю
по модулю  не существует. Например, обратного к 2 по модулю 10 не существует: при умножении любого числа
не существует. Например, обратного к 2 по модулю 10 не существует: при умножении любого числа  на 2 мы не получим 1 по модулю 10. Если модуль сравнения
на 2 мы не получим 1 по модулю 10. Если модуль сравнения  - простое число, то обратный элемент есть для каждого числа.
- простое число, то обратный элемент есть для каждого числа.
Пример 1.23 Найдем число, обратное к 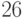 по модулю
по модулю 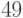 .
.
Числа 26 и 49 взаимно просты, поэтому искомое число существует. Реализуем расширенный алгоритм Евклида для чисел 26 и 49.
И теперь 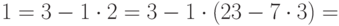 . Итак,
. Итак, 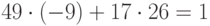 . То есть
. То есть 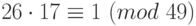 . Таким образом, число 17 является обратным к 26 по модулю 49.
. Таким образом, число 17 является обратным к 26 по модулю 49.
1.2.4 Решение сравнений
Сравнение с одним неизвестным  имеет вид
имеет вид
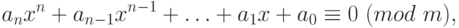 |
( 1.3) |
где  ,
,  . Если
. Если 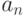 не делится на
не делится на  , то
, то  называется степенью сравнения (1.3).
называется степенью сравнения (1.3).
Определение 1.15 Решением сравнения (1.3) называется всякое целое число 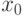 , для которого
, для которого 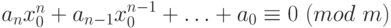 .
.
Если 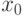 удовлетворяет сравнению (1.3), то, согласно свойству 11 сравнений, этому сравнению будут удовлетворять все целые числа, сравнимые с
удовлетворяет сравнению (1.3), то, согласно свойству 11 сравнений, этому сравнению будут удовлетворять все целые числа, сравнимые с 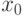 по модулю
по модулю  . Поэтому все числа, сравнимые по модулю
. Поэтому все числа, сравнимые по модулю  с
с 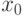 , будем рассматривать как одно решение. Другими словами, решениями сравнения (1.3) будут классы чисел. Например,
, будем рассматривать как одно решение. Другими словами, решениями сравнения (1.3) будут классы чисел. Например, 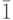 - это класс единицы, то есть все числа, сравнимые с 1,
- это класс единицы, то есть все числа, сравнимые с 1, 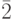 - класс числа 2, то есть все числа, сравнимые с 2, т.д. И фразу "данное сравнение имеет 2 решения" надо понимать так: данному сравнению удовлетворяют два класса чисел. Как отмечалось выше, эти классы не имеют общих элементов. В дальнейшем мы записываем какое-либо число - представитель класса без черты сверху, называя это число решением.
- класс числа 2, то есть все числа, сравнимые с 2, т.д. И фразу "данное сравнение имеет 2 решения" надо понимать так: данному сравнению удовлетворяют два класса чисел. Как отмечалось выше, эти классы не имеют общих элементов. В дальнейшем мы записываем какое-либо число - представитель класса без черты сверху, называя это число решением.
Сравнения, множества решений которых совпадают, называются равносильными.

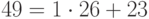 ,
,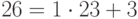 ,
,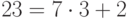 ,
,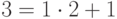 .
.