|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на основе спинового магнитного резонанса
Введение
В данной лекции мы рассмотрим несколько перспективных вариантов реализации квантового процессора на основе явления спинового магнитного резонанса. Именно на них в начале ХХІ в. возлагались наибольшие надежды.
Как мы уже отметили в предыдущей лекции, спин атомного ядра, электрона или другой элементарной частицы в конце ХХ в. рассматривался как один из наиболее естественных вариантов реализации кубита. Прежде, чем ознакомить вас с предложенными конструкциями квантовых процессоров на основе явления спинового магнитного резонанса, напомним вкратце сведения о поведении ядра или элементарной частицы с не нулевым спином и соответственно с не нулевым магнитным моментом во внешнем магнитном поле.
Поведение "спиновых" кубитов в магнитном поле
Расщепление вырожденного квантового состояния
Квантово-механический анализ этого поведения показывает, что во внешнем магнитном поле каждое разрешенное (при отсутствии магнитного поля) стационарное состояние частицы со спином  расщепляется на
расщепляется на 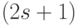 разрешенных состояний. Строго говоря, с самого начала это не одно, а
разрешенных состояний. Строго говоря, с самого начала это не одно, а 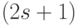 разрешенных состояний с разными значениями спинового квантового числа. Но при отсутствии магнитного поля они не отличаются между собой по энергии, "вырождены". А вот при наличии внешнего магнитного поля "вырождение" снимается, и эти разные состояния уже явным образом отличаются по энергии и по ориентации магнитного момента частицы относительно этого поля.
разрешенных состояний с разными значениями спинового квантового числа. Но при отсутствии магнитного поля они не отличаются между собой по энергии, "вырождены". А вот при наличии внешнего магнитного поля "вырождение" снимается, и эти разные состояния уже явным образом отличаются по энергии и по ориентации магнитного момента частицы относительно этого поля.
На
рис.
9.1 показано расщепление разрешенного уровня энергии частицы в постоянном магнитном поле с индукцией  и соответствующие каждому разрешенному энергетическому уровню ориентации вектора магнитного момента относительно направления поля при нескольких разных значениях спина
и соответствующие каждому разрешенному энергетическому уровню ориентации вектора магнитного момента относительно направления поля при нескольких разных значениях спина  .
.
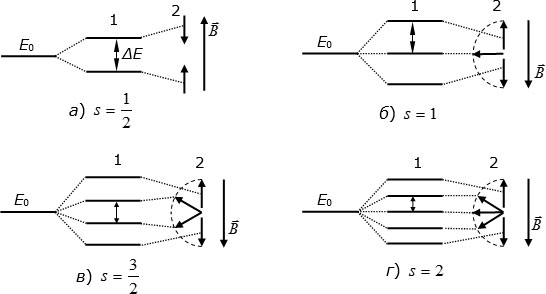
Рис. 9.1. Расщепление энергетического уровня частицы со спином в постоянном магнитном поле: 1 – расщепленные энергетические уровни; 2 – разрешенные ориентации магнитного момента относительно направления поля
При значении спина 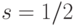 (
рис.
9.1.а) каждый разрешенный энергетический уровень расщепляется на 2 разрешенных уровня, нижнему из которых соответствует ориентация магнитного момента
(
рис.
9.1.а) каждый разрешенный энергетический уровень расщепляется на 2 разрешенных уровня, нижнему из которых соответствует ориентация магнитного момента 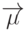 частицы параллельно, а верхнему – антипараллельно вектору
частицы параллельно, а верхнему – антипараллельно вектору  . Оба энергетических уровня отстоят от первоначального уровня
. Оба энергетических уровня отстоят от первоначального уровня 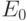 на величину
на величину  . Энергетическое расстояние между разрешенными уровнями
. Энергетическое расстояние между разрешенными уровнями
 |
( 9.1) |
 – т.н. гиромагнитное отношение для данной частицы,
– т.н. гиромагнитное отношение для данной частицы, 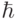 – известная константа (приведенная постоянная Планка),
– известная константа (приведенная постоянная Планка), 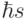 – механический вращательный момент частицы со спином
– механический вращательный момент частицы со спином  . В частности для свободного электрона
. В частности для свободного электрона
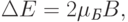 |
( 9.2) |
 Дж/Тл – магнитный спиновый момент электрона, который называют магнетоном Бора. Заметим, что для электрона (из-за отрицательного знака его электрического заряда) гиромагнитное отношение отрицательное, т.е. магнитный момент электрона направлен противоположно механическому орбитальному моменту. У положительно заряженных атомных ядер направления механического и магнитного моментов совпадают, но величина гиромагнитного отношения намного меньше. Из-за этого магнитный момент ядер намного меньше магнитного момента электронов с таким же спином.
Дж/Тл – магнитный спиновый момент электрона, который называют магнетоном Бора. Заметим, что для электрона (из-за отрицательного знака его электрического заряда) гиромагнитное отношение отрицательное, т.е. магнитный момент электрона направлен противоположно механическому орбитальному моменту. У положительно заряженных атомных ядер направления механического и магнитного моментов совпадают, но величина гиромагнитного отношения намного меньше. Из-за этого магнитный момент ядер намного меньше магнитного момента электронов с таким же спином.При значении спина 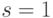 (
рис.
9.1.б) каждый разрешенный энергетический уровень расщепляется на 3 разрешенных энергетических уровня, которым соответствует ориентация магнитного момента
(
рис.
9.1.б) каждый разрешенный энергетический уровень расщепляется на 3 разрешенных энергетических уровня, которым соответствует ориентация магнитного момента 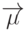 частицы параллельно, ортогонально или противоположно к вектору
частицы параллельно, ортогонально или противоположно к вектору  . Состоянию с ориентацией
. Состоянию с ориентацией 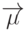 параллельно к вектору
параллельно к вектору  соответствует уровень энергии, лежащий ниже начального уровня
соответствует уровень энергии, лежащий ниже начального уровня 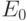 на величину
на величину  , состоянию с ориентацией
, состоянию с ориентацией 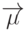 противоположно вектору
противоположно вектору  – уровень энергии, расположенный выше
– уровень энергии, расположенный выше 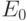 на такую же величину, а состоянию с ортогональной ориентацией – уровень энергии, равный
на такую же величину, а состоянию с ортогональной ориентацией – уровень энергии, равный 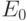 .
.
При значении спина 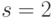 (
рис.
9.1.г) каждый разрешенный энергетический уровень расщепляется на 5 разрешенных энергетических уровней с ориентацией магнитного момента
(
рис.
9.1.г) каждый разрешенный энергетический уровень расщепляется на 5 разрешенных энергетических уровней с ориентацией магнитного момента 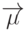 частицы параллельно или противоположно к вектору
частицы параллельно или противоположно к вектору  , ортогонально или под углами
, ортогонально или под углами  и
и  к нему. Энергетическое расстояние между соседними разрешенными уровнями, как и в предыдущих случаях, определяется формулой (10.1).
к нему. Энергетическое расстояние между соседними разрешенными уровнями, как и в предыдущих случаях, определяется формулой (10.1).
Свойства простейшего спинового кубита
При использовании для реализации кубита ядерных спинов, как правило, используют ядра с наименьшим полуцелым спином 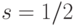 . В этом случае энергетическая схема наиболее проста, и поэтому легче разобраться с квантовым поведением такого кубита.
. В этом случае энергетическая схема наиболее проста, и поэтому легче разобраться с квантовым поведением такого кубита.
Простейший спиновый кубит имеет два базовых состояния, которым соответствуют два уровня энергии, изображенные на
рис.
9.2. Маленькими стрелками показана ориентация магнитного момента кубита в каждом состоянии. Справа показан общепринятый вариант кодирования этих состояний: нижний уровень энергии соответствует состоянию 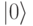 , верхний – состоянию
, верхний – состоянию 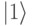 .
.
В гибридных состояниях ориентация магнитного момента кубита относительно постоянного магнитного поля  задается двумя углами
задается двумя углами 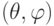 , которые отсчитываются от направления магнитного поля так, как принято в сферической системе координат и как было показано в
"Квантовые процессоры на основе спинового магнитного резонанса"
на сфере Блоха (см.
рис.
9.1).
, которые отсчитываются от направления магнитного поля так, как принято в сферической системе координат и как было показано в
"Квантовые процессоры на основе спинового магнитного резонанса"
на сфере Блоха (см.
рис.
9.1).
Квантово-механический расчет (так же, как и классический) показывает, что влияние постоянного магнитного поля  на магнитный момент
на магнитный момент 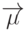 кубита при наличии у микрочастицы механического момента вращения (
кубита при наличии у микрочастицы механического момента вращения (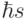 ) приводит к прецессии магнитного момента вокруг направления магнитного поля с частотой
) приводит к прецессии магнитного момента вокруг направления магнитного поля с частотой
 |
( 9.3) |
 магнитного момента
магнитного момента 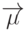 не является фиксированным, а все время изменяется по закону
не является фиксированным, а все время изменяется по закону
 |
( 9.4) |
Разные гибридные состояния кубита с одинаковым углом  различаются начальной фазой
различаются начальной фазой  .
.
В собственной системе координат вектор состояния (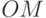 на
рис.
9.1) остается неподвижным и характеризуется парой углов
на
рис.
9.1) остается неподвижным и характеризуется парой углов 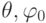 . Это – т.н. подвижная система координат (ПСК), которая вращается вместе с вектором
. Это – т.н. подвижная система координат (ПСК), которая вращается вместе с вектором 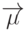 с частотой ларморовой прецессии вокруг направления магнитного поля.
с частотой ларморовой прецессии вокруг направления магнитного поля.

