Процедуры и функции - методы класса
Классификация чисел
Числа разделяются на классы. Целые положительные числа - N = {1, 2, 3, … } - составляют множество натуральных чисел. Зачастую и 0 считают натуральным числом.
Множество целых чисел Z включает в себя все натуральные числа, число 0 и все натуральные числа, взятые со знаком минус: Z = {0, 1, -1, 2, -2, …}.
Каждое рациональное число x можно задать парой целых чисел (m, n), где m является числителем, n - знаменателем числа: x = m/n. Эквивалентным представлением рационального числа является его задание в виде числа, записанного в позиционной десятичной системе счисления, где дробная часть числа может быть конечной или бесконечной периодической дробью. Например, число x = 1/3 = 0,(3) представляется бесконечной периодической дробью.
Числа, задаваемые бесконечными непериодическими дробями, называются иррациональными числами. Таковыми являются, например, все числа вида vp, где p - простое число. Иррациональными являются известные всем числа  и e.
и e.
Объединение множеств целых, рациональных и иррациональных чисел составляет множество вещественных чисел. Геометрическим образом множества вещественных чисел является прямая линия - вещественная ось, где каждой точке оси соответствует некоторое вещественное число, так что вещественные числа плотно и непрерывно заполняют всю вещественную ось.
Плоскость представляет геометрический образ множества комплексных чисел, где вводятся уже две оси - вещественная и мнимая. Каждое комплексное число, задаваемое парой вещественных чисел, представимо в виде: x = a+b*i, где a и b - вещественные числа, которые можно рассматривать как декартовы координаты числа на плоскости.
Делители и множители
Рассмотрим сейчас классификацию, которая делит множество натуральных чисел на два подмножества - простых и составных чисел. В основе этой классификации лежит понятие делимости натуральных чисел. Если n делится нацело на d, то говорят, что d "делит" n, и записывают это в виде:  . Заметьте, это определение, возможно, не соответствует интуитивному пониманию: d "делит" n, если n делится на d, а не наоборот. Число d называется делителем числа n. У каждого числа n есть два тривиальных делителя - 1 и n. Делители, отличные от тривиальных, называются множителями числа n. Число n называется простым, если у него нет делителей, отличных от тривиальных. Простые числа делятся только на 1 и сами на себя. Числа, у которых есть множители, называются составными. Число 1 является особым числом, поскольку не относится ни к простым, ни к составным числам. Отрицательные числа также не относятся ни к простым, ни к составным,
но всегда можно рассматривать модуль числа и относить его к простым или составным числам.
. Заметьте, это определение, возможно, не соответствует интуитивному пониманию: d "делит" n, если n делится на d, а не наоборот. Число d называется делителем числа n. У каждого числа n есть два тривиальных делителя - 1 и n. Делители, отличные от тривиальных, называются множителями числа n. Число n называется простым, если у него нет делителей, отличных от тривиальных. Простые числа делятся только на 1 и сами на себя. Числа, у которых есть множители, называются составными. Число 1 является особым числом, поскольку не относится ни к простым, ни к составным числам. Отрицательные числа также не относятся ни к простым, ни к составным,
но всегда можно рассматривать модуль числа и относить его к простым или составным числам.
Любое составное число N можно представить в виде произведения его множителей: 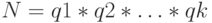 . Это представление не единственно, например 96 = 8*12 = 2*3*16. Однако для каждого составного числа N существует единственное представление в виде произведения степеней простых чисел:
. Это представление не единственно, например 96 = 8*12 = 2*3*16. Однако для каждого составного числа N существует единственное представление в виде произведения степеней простых чисел: 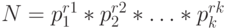 , где
, где 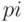 - простые числа и
- простые числа и 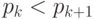 . Это представление называется разложением числа N на простые множители. Например
. Это представление называется разложением числа N на простые множители. Например  .
.
Если 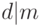 и
и  , то d является общим делителем чисел m и n. Среди всех общих делителей можно выделить наибольший общий делитель, обозначаемый как НОД(m,n). Если НОД(m,n) = 1, то числа m и n называются взаимно простыми. Простые числа взаимно просты, так что НОД(q,p) =1, если q и p - простые числа.
, то d является общим делителем чисел m и n. Среди всех общих делителей можно выделить наибольший общий делитель, обозначаемый как НОД(m,n). Если НОД(m,n) = 1, то числа m и n называются взаимно простыми. Простые числа взаимно просты, так что НОД(q,p) =1, если q и p - простые числа.
Если 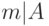 и
и  , то A является общим кратным чисел m и n. Среди всех общих кратных можно выделить наименьшее общее кратное, обозначаемое как НОК(m,n). Если НОК(m,n) = m*n, то числа m и n являются взаимно простыми. НОК(q, p) =q*p, если q и p - простые числа.
, то A является общим кратным чисел m и n. Среди всех общих кратных можно выделить наименьшее общее кратное, обозначаемое как НОК(m,n). Если НОК(m,n) = m*n, то числа m и n являются взаимно простыми. НОК(q, p) =q*p, если q и p - простые числа.
Если через 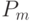 и
и 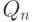 обозначить множества всех простых множителей чисел m и n, то
обозначить множества всех простых множителей чисел m и n, то

Если получено разложение чисел m и n на простые множители, то, используя приведенные соотношения, нетрудно вычислить НОД(m,n) и НОК(m,n). Существуют и более эффективные алгоритмы, не требующие разложения числа на множители.
Алгоритм Эвклида
Эффективный алгоритм вычисления НОД(m,n) предложен еще Эвклидом. Он основывается на следующих свойствах НОД(m,n), доказательство которых предоставляется читателю:
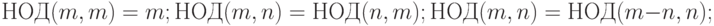
Если  , то по третьему свойству его можно уменьшить на величину n. Если же
, то по третьему свойству его можно уменьшить на величину n. Если же  , то по второму свойству аргументы можно поменять местами и вновь придти к ранее рассмотренному случаю. Когда же в результате этих преобразований значения аргументов сравняются, то решение будет найдено. Поэтому можно предложить следующую схему:
, то по второму свойству аргументы можно поменять местами и вновь придти к ранее рассмотренному случаю. Когда же в результате этих преобразований значения аргументов сравняются, то решение будет найдено. Поэтому можно предложить следующую схему:
while(m != n)
{
if(m < n) swap(m,n);
m = m - n;
}
return(m);Здесь процедура swap выполняет обмен значениями аргументов.
Если немного подумать, то становится ясно, что вовсе не обязательно обмениваться значениями - достаточно на каждом шаге цикла изменять аргумент с максимальным значением. В результате приходим к схеме:
while(m != n)
{
if(m > n) m = m - n;
else n = n - m;
}
return(m);Если еще немного подумать, то можно улучшить и эту схему, перейдя к циклу с тождественно истинным условием:
while(true)
{
if(m > n) m = m - n;
else if (n > m) n = n - m;
else return(m);
}Последняя схема хороша тем, что в ней отчетливо видна необходимость доказательства завершаемости этого цикла. Доказать завершаемость цикла нетрудно, используя понятие варианта цикла. Для данного цикла вариантом может служить целочисленная функция - max(m,n), которая уменьшается на каждом шаге, оставаясь всегда положительной.
Достоинством данной версии алгоритма Эвклида является и то, что на каждом шаге используется элементарная и быстрая операция над целыми числами - вычитание. Если допустить операцию вычисления остатка при делении нацело, то число шагов цикла можно существенно уменьшить. Справедливо следующее свойство:
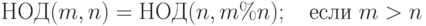
Это приводит к следующей схеме:
int temp;
if(n>m) temp = m; m = n; n = temp; //swap(m,n)
while(m != n)
{
temp = m; m = n; n = temp%n;
}Если немного подумать, то становится ясно, что вовсе не обязательно выполнять проверку перед началом цикла. Это приводит к более простой схеме вычисления НОД, применяемой обычно на практике:
int temp;
while(m != n)
{
temp = m; m = n; n = temp%n;
}Для вычисления НОК(m, n) можно воспользоваться следующим соотношением:
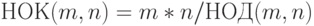
А можно ли вычислить НОК(m, n), не используя операций умножения и деления? Оказывается, можно одновременно с вычислением НОД(m,n) вычислять и НОК(m,n). Вот соответствующая схема:
int x = v = m, y = u = n,;
while(x != y)
{
if(x > y){ x = x - y; v = v + u;}
else {y = y - x; u = u + v;}
}
НОД = (x + y)/2; НОК = (u+v)/2;Доказательство того, что эта схема корректно вычисляет НОД, следует из ранее приведенных свойств НОД. Менее очевидна корректность вычисления НОК. Для доказательства заметьте, что инвариантом цикла является следующее выражение:
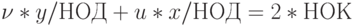
Это соотношение выполняется после инициализации переменных до начала выполнения цикла. По завершении цикла, когда x и y становятся равными НОД, из истинности инварианта следует корректность схемы. Нетрудно проверить, что операторы тела цикла оставляют утверждение истинным. Детали доказательства оставляются читателям.
Понятие НОД и НОК можно расширить, определив их для всех целых чисел. Справедливы следующие соотношения:
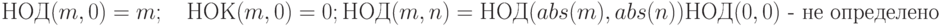
Расширенный алгоритм Эвклида
Иногда полезно представлять НОД(m,n) в виде линейной комбинации m и n:

В частности, вычисление коэффициентов a и b необходимо в алгоритме RSA - шифрования с открытым ключом. Приведу схему алгоритма, позволяющую вычислить тройку - d, a, b - наибольший общий делитель и коэффициенты разложения. Алгоритм удобно реализовать в виде рекурсивной процедуры
ExtendedEuclid(int m, int n, ref int d, ref int a, ref int b),
которая по заданным входным аргументам m и n вычисляет значения аргументов d, a, b. Нерекурсивная ветвь этой процедуры соответствует случаю n = 0, возвращая в качестве результата значения: d = m, a = 1, b = 0. Рекурсивная ветвь вызывает
ExtendedEuclid(n, m % n, ref d, ref a, ref b)
и затем изменяет полученные в результате вызова значения a и b следующим образом:

Доказательство корректности этого алгоритма построить нетрудно. Для нерекурсивной ветви корректность очевидна, а для рекурсивной ветви нетрудно показать, что из истинности результата, возвращаемого при рекурсивном вызове, следует его истинность для входных аргументов после пересчета значений a и b.
Как работает эта процедура? Вначале происходит рекурсивный спуск, пока n не станет равно нулю.
В этот момент впервые будет вычислено значение d и значения параметров a и b. После этого начнется подъем и будут перевычисляться параметры a и b.
Задачи
- 49. Даны m и n - натуральные числа. Вычислите НОД(m, n). При вычислениях не используйте операций умножения и деления.
- 50. Даны m и n - натуральные числа. Вычислите НОК(m, n).
- 51. Даны m и n - натуральные числа. Вычислите НОК(m, n). При вычислениях не используйте операций умножения и деления.
- 52. Даны m и n - целые числа. Вычислите НОД(m, n). При вычислениях не используйте операций умножения и деления.
- 53. Даны m и n - целые числа. Вычислите НОК(m, n). При вычислениях не используйте операций умножения и деления.
- 54. Даны m и n - целые числа. Вычислите НОД(m, n). При вычислениях используйте операцию взятия остатка от деления нацело.
- 55. Даны m и n - целые числа. Вычислите НОК(m, n). При вычислениях используйте операцию взятия остатка от деления нацело.
- 56. Даны m и n - целые числа. Вычислите тройку чисел - (d, a, b), используя расширенный алгоритм Эвклида.
- 57. Даны m и n - натуральные числа. Представьте НОД(m, n) в виде линейной комбинации m и n.
- 58. Даны m и n - целые числа. Представьте НОД(m, n) в виде линейной комбинации m и n.
- 59. Даны m и n - целые числа. Проверьте, являются ли числа m и n взаимно простыми.
Простые числа
Среди четных чисел есть только одно простое число - это 2. Простых нечетных чисел сколь угодно много. Нетрудно доказать, что число 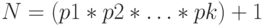 , где
, где 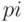 - подряд идущие простые числа, является простым. Так что, если построено
- подряд идущие простые числа, является простым. Так что, если построено  простых чисел, то можно построить еще одно простое число
простых чисел, то можно построить еще одно простое число  , большее
, большее 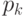 . Отсюда следует, что множество простых чисел неограниченно. Пример: число N = 2*3*5*7 + 1 = 211 является простым числом.
. Отсюда следует, что множество простых чисел неограниченно. Пример: число N = 2*3*5*7 + 1 = 211 является простым числом.
Решето Эратосфена
Как определить, что число N является простым? Если допустима операция N % m, дающая остаток от деления числа N на число m, то простейший алгоритм состоит в проверке того, что остаток не равен нулю при делении числа N на все числа m, меньшие N. Очевидным улучшением этого алгоритма является сокращение диапазона проверки - достаточно рассматривать числа m в диапазоне [2, vN].
Еще в 3-м веке до н.э. греческий математик Эратосфен предложил алгоритм нахождения простых чисел в диапазоне [3, N], не требующий операций деления. Этот алгоритм получил название "Решето Эратосфена". В компьютерном варианте идею этого алгоритма можно описать следующим образом. Построим массив Numbers, элементы которого содержат подряд идущие нечетные числа, начиная с 3. Вначале все числа этого массива считаются невычеркнутыми. Занесем первое невычеркнутое число из этого массива в массив SimpleNumbers - и это будет первое нечетное простое число (3). Затем выполним просеивание, проходя по массиву Numbers с шагом, равным найденному простому числу, вычеркивая все попадающиеся при этом проходе числа. При первом проходе будет вычеркнуто число 3 и все числа, кратные 3. На следующем проходе в таблицу простых чисел будет занесено следующее простое число 5, а из массива Numbers будут вычеркнуты числа, кратные 5. Процесс повторяется, пока не будут вычеркнуты все числа в массиве Numbers. В результате массив SimpleNumbers будет содержать таблицу первых простых чисел, меньших N.
Этот алгоритм хорош для нахождения сравнительно небольших простых чисел. Но если потребуется найти простое число с двадцатью значащими цифрами, то памяти компьютера уже не хватит для хранения соответствующих массивов. Замечу, что в современных алгоритмах шифрования используются простые числа, содержащие несколько сотен цифр.
Плотность простых чисел
Мы показали, что число простых чисел неограниченно. Понятно, что их меньше, чем нечетных чисел, но насколько меньше? Какова плотность простых чисел? Пусть  - это функция, возвращающая число простых чисел, меньших n. Точно задать эту функцию не удается, но для нее есть хорошая оценка. Справедлива следующая теорема:
- это функция, возвращающая число простых чисел, меньших n. Точно задать эту функцию не удается, но для нее есть хорошая оценка. Справедлива следующая теорема:
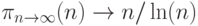
Функция  асимптотически сверху приближается к своему пределу, так что оценка дает слегка заниженные значения. Эту оценку можно использовать в алгоритме решета Эратосфена для выбора размерности массива SimpleNumbers, когда задана размерность массива Numbers, и, наоборот, при заданной размерности таблицы простых чисел можно выбрать подходящую размерность для массива Numbers.
асимптотически сверху приближается к своему пределу, так что оценка дает слегка заниженные значения. Эту оценку можно использовать в алгоритме решета Эратосфена для выбора размерности массива SimpleNumbers, когда задана размерность массива Numbers, и, наоборот, при заданной размерности таблицы простых чисел можно выбрать подходящую размерность для массива Numbers.
Табличный алгоритм определения простоты чисел
Если хранить таблицу простых чисел SimpleNumbers, в которой наибольшее простое число равно M, то достаточно просто определить, является ли число N, меньшее 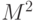 , простым. Если N меньше M, то достаточно проверить, находится ли число N в таблице SimpleNumbers. Если N больше M, то достаточно проверить, делится ли число N на числа из таблицы SimpleNumbers, не превосходящие значения vN. Понятно, что если у числа N нет простых множителей, меньших vN, то число N является простым.
, простым. Если N меньше M, то достаточно проверить, находится ли число N в таблице SimpleNumbers. Если N больше M, то достаточно проверить, делится ли число N на числа из таблицы SimpleNumbers, не превосходящие значения vN. Понятно, что если у числа N нет простых множителей, меньших vN, то число N является простым.
Использование таблицы простых чисел требует соответствующей памяти компьютера, а следовательно, ограничивает возможности этого алгоритма, не позволяя использовать его для нахождения больших простых чисел.
Тривиальный алгоритм
Если N - нечетное число, то проверить, что оно является простым, можно на основе определения простоты числа. При этом не требуется никакой памяти для хранения таблиц чисел, - но, как всегда, выигрывая в памяти, мы проигрываем во времени. Действительно, достаточно проверить, делится ли нацело число N на подряд идущие нечетные числа в диапазоне [3, vN]. Если у числа N есть хоть один множитель, то оно составное, иначе - простое.
Все рассмотренные алгоритмы перестают эффективно работать, когда числа выходят за пределы разрядной сетки компьютера, отведенной для представления чисел, так что если возникает необходимость работы с целыми числами, выходящими за пределы диапазона System.Int64, то задача определения простоты такого числа становится совсем не простой. Существуют некоторые рецепты, позволяющие определить, что число является составным. Вспомним хотя бы известные со школьных времен алгоритмы. Если последняя цифра числа делится на 2, то и число делится на 2. Если две последние цифры числа делятся на 4, то и число делится на 4. Если сумма цифр делится на 3 (на 9), то и число делится на 3 (на 9). Если последняя цифра равна 0 или 5, то число делится на 5. Математики затратили много усилий, доказывая, что то или иное число является (или не является) простым числом. Сейчас есть особые приемы, позволяющие доказать, что числа некоторого вида являются простыми.
Наиболее подходящими кандидатами на простоту являются числа вида 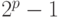 , где p - это простое число. Например, доказано, что число
, где p - это простое число. Например, доказано, что число  , имеющее более 6000 цифр, является простым, но нельзя сказать, какие простые числа являются ближайшими соседями этого числа.
, имеющее более 6000 цифр, является простым, но нельзя сказать, какие простые числа являются ближайшими соседями этого числа.
Задачи
- 60. Дано целое N. Используя алгоритм решета Эратосфена, найдите все простые числа, меньшие N.
- 61. Дано целое N. Используя алгоритм решета Эратосфена, найдите N первых простых чисел.
- 62. Дана таблица, содержащая N первых простых чисел. По заданному n < N вычислите разность между функцией
 и ее оценкой - n/ln(n).
и ее оценкой - n/ln(n). - 63. Дана таблица, содержащая N первых простых чисел. Используя табличный алгоритм, вычислите все простые числа в диапазоне [M+1, M*M], где M - наибольшее простое число, хранимое в таблице.
- 64. Дано целое N. Постройте таблицу, содержащую N первых нечетных простых чисел. Используйте табличный алгоритм с постепенным заполнением таблицы, начиная со случая, когда в ней хранится только одно простое число 3.
- 65. Дано число N. Определите, является ли оно простым, используя тривиальный алгоритм.
- 66. Дано число N. Определите его первый простой множитель, если он существует.
Проекты
- 67. Построить класс "Температура", позволяющий задавать температуру в разных единицах измерения. Построить Windows-проект, поддерживающий интерфейс для работы с классом.
- 68. Построить класс "Расстояния", позволяющий использовать разные системы мер. Построить Windows-проект, поддерживающий интерфейс для работы с классом.
- 69. Построить класс "Простые числа". Построить Windows-проект, поддерживающий интерфейс для работы с классом.
- 70. Построить класс "Системы счисления". Построить Windows-калькулятор, поддерживающий вычисления в заданной системе счисления.
- 71. Построить класс "Рациональные числа". Построить Windows-калькулятор, поддерживающий вычисления с этими числами.
- 72. Построить класс "Комплексные числа". Построить Windows-калькулятор, поддерживающий вычисления с этими числами.
