|
Упражнение 2.1.25 |
Основные свойства контекстно-свободных языков
9.4. Свойства замкнутости класса контекстно-свободных языков
Теорема 9.4.1. Если L - контекстно-свободный язык, то L* тоже контекстно-свободный язык.
Доказательство.
Пусть язык L
порождается контекстно-свободной грамматикой 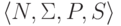 .
Тогда язык L*
порождается грамматикой
.
Тогда язык L*
порождается грамматикой
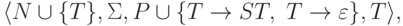
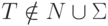 .
.Теорема 9.4.2. Если L1
и L2 - контекстно-свободные языки над алфавитом  ,
то
,
то 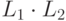 тоже контекстно-свободный язык.
тоже контекстно-свободный язык.
Доказательство.
Пусть язык L1
порождается контекстно-свободной грамматикой 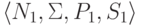 и L2
порождается контекстно-свободной грамматикой
и L2
порождается контекстно-свободной грамматикой 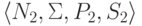 ,
где
,
где 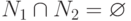 .
Тогда
.
Тогда 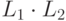 порождается грамматикой
порождается грамматикой

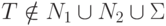 .
.Теорема 9.4.3. Если L1 и L2 - контекстно-свободные языки над алфавитом  , то
, то 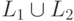 тоже контекстно-свободный язык.
тоже контекстно-свободный язык.
Доказательство.
Пусть язык L1
порождается контекстно-свободной грамматикой 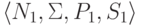 и L2
порождается контекстно-свободной грамматикой
и L2
порождается контекстно-свободной грамматикой 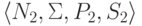 ,
где
,
где 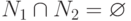 .
Тогда
.
Тогда 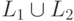 порождается грамматикой
порождается грамматикой
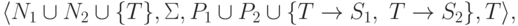
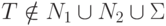 .
.Теорема 9.4.4. Если L - контекстно-свободный язык, то 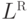 тоже контекстно-свободный язык.
тоже контекстно-свободный язык.
Упражнение 9.4.5. Является ли контекстно-свободным язык  ?
?
Упражнение 9.4.6.
Найти контекстно-свободную грамматику для языка 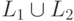 ,
где L1
порождается грамматикой
,
где L1
порождается грамматикой


9.5. Пересечение и дополнение контекстно-свободных языков
Теорема 9.5.1. Неверно, что для любых контекстно-свободных языков L1 и L2 язык 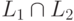 тоже контекстно-свободный.
тоже контекстно-свободный.
Доказательство.
Положим 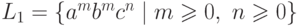 и
и 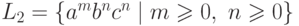 .
В примере 9.2.1
было доказано, что язык
.
В примере 9.2.1
было доказано, что язык 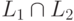 не является контекстно-свободным.
не является контекстно-свободным.
Теорема 9.5.2. Неверно, что для любого контекстно-свободного языка  язык
язык  тоже контекстно-свободный.
тоже контекстно-свободный.
Доказательство.
Положим 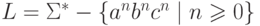 ,
где
,
где 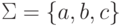 .
В примере 9.3.4
было доказано, что язык L
является линейным
(и следовательно, контекстно-свободным).
.
В примере 9.3.4
было доказано, что язык L
является линейным
(и следовательно, контекстно-свободным).
Упражнение 9.5.3. Является ли контекстно-свободным язык 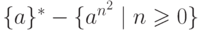 ?
?
Упражнение 9.5.4. Является ли контекстно-свободным язык 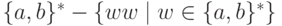 ?
?
Упражнение 9.5.5. Существует ли такой
линейный язык L
над алфавитом {a,b},
что язык 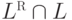 не является контекстно-свободным?
не является контекстно-свободным?
