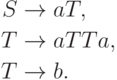|
Упражнение 2.1.25 |
Нормальные формы контекстно-свободных грамматик
8.4*. Нормальная форма Грейбах
Определение 8.4.1. Грамматика в нормальной форме Грейбах
(grammar in Greibach normal form) -
контекстно-свободная грамматика 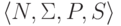 ,
в которой каждое правило имеет один из следующих четырех видов:
,
в которой каждое правило имеет один из следующих четырех видов:  ,
, 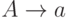 ,
,  ,
, 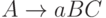 ,
где
,
где 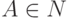 ,
, 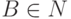 ,
, 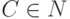 ,
,  .
.
Пример 8.4.2. Грамматика
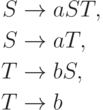
Замечание 8.4.3.
Некоторые авторы разрешают
в грамматиках в нормальной форме Грейбах
использовать также правила вида  ,
где
,
где 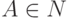 ,
,  ,
, 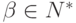 (в определении 8.4.1
разрешены, только если
(в определении 8.4.1
разрешены, только если  ).
).
Теорема 8.4.4. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Грейбах.
Доказательство.
Докажем теорему для контекстно-свободных языков,
не содержащих пустого слова.
Согласно теореме 8.3.5
исходный язык порождается некоторой грамматикой 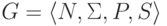 ,
в которой каждое правило имеет вид
,
в которой каждое правило имеет вид 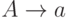 или
или 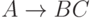 ,
где
,
где 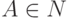 ,
, 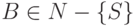 ,
, 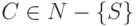 ,
,  .
.
Введем |N|2
новых вспомогательных символов, соответствующих упорядоченным парам
из множества  .
Новый символ, соответствующий паре
.
Новый символ, соответствующий паре 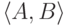 ,
будем обозначать (A\B).
Построим грамматику "почти в нормальной форме Грейбах"
,
будем обозначать (A\B).
Построим грамматику "почти в нормальной форме Грейбах" 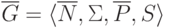 ,
положив
,
положив 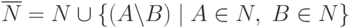 и
и
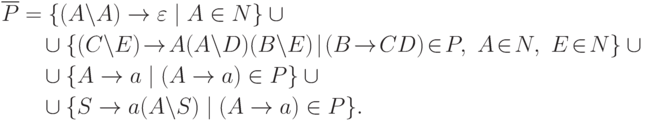
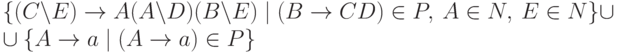
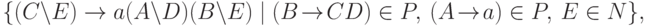
 .
.Сначала проверим индукцией по длине слова 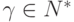 ,
что если
,
что если 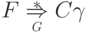 ,
то
,
то 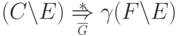 для любого
для любого 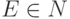 .
Чтобы провести шаг индукции, допустим, что
.
Чтобы провести шаг индукции, допустим, что  и
и

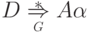 и
и 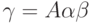 .
По предположению индукции имеем
.
По предположению индукции имеем 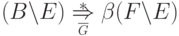 и
и 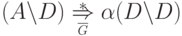 .
Подключая эти выводы к правилу
.
Подключая эти выводы к правилу  и используя
и используя 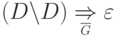 ,
получаем искомый вывод
,
получаем искомый вывод  .
.Докажем теперь, что для любого 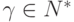 равносильны утверждения
равносильны утверждения 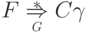 и
и  .
В одну сторону это следует из только что доказанного.
Доказательство того,
что если
.
В одну сторону это следует из только что доказанного.
Доказательство того,
что если  ,
то
,
то 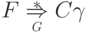 ,
проведем
индукцией по длине слова
,
проведем
индукцией по длине слова 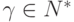 .
Чтобы провести шаг индукции, допустим, что
.
Чтобы провести шаг индукции, допустим, что  ,
,  ,
, 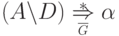 ,
, 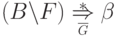 и
и 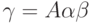 .
По предположению индукции
.
По предположению индукции 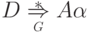 и
и 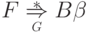 .
Получаем искомый вывод
.
Получаем искомый вывод

Теперь убедимся, что  .
Рассмотрим произвольное слово
.
Рассмотрим произвольное слово 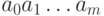 ,
где
,
где 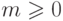 и
и 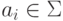 для всех
для всех 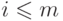 .
Пусть
.
Пусть
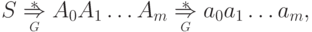
 для всех
для всех 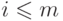 .
Тогда
.
Тогда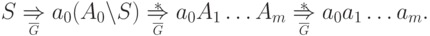
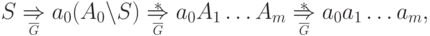
 для всех
для всех 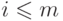 .
Тогда
.
Тогда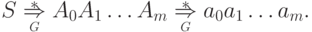
Пример 8.4.5. Грамматика

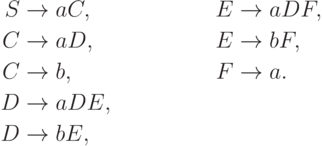
Теорема 8.4.6. Пусть язык L контекстно-свободный. Тогда язык 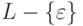 порождается некоторой грамматикой в нормальной форме Грейбах без
порождается некоторой грамматикой в нормальной форме Грейбах без  - правил.
- правил.
Пример 8.4.7. Грамматика
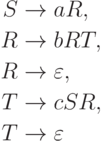
 -правил:
-правил: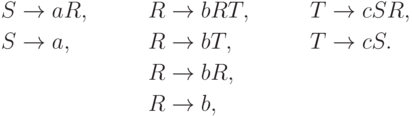
Упражнение 8.4.8. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
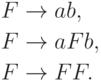
Упражнение 8.4.9. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
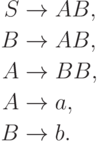
Упражнение 8.4.10. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
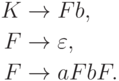
Упражнение 8.4.11. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике