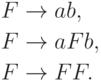НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 9: Нормальные формы контекстно-свободных грамматик

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 2521 / 1036 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.2. Устранение эпсилон-правил

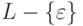Теорема 8.2.1. Пусть язык является контекстно-свободным. Тогда язык $L \sminus \{ \varepsilon \}$ порождается некоторой контекстно-свободной грамматикой без $\varepsilon$ - правил.

Доказательство. Пусть дана контекстно-свободная грамматика 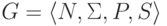$G = \lalg N , \Sigma , P , S \ralg$ , порождающая язык L. Проведем серию преобразований множества P.

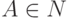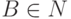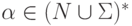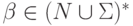Если для каких-то $A \in N$ , $B \in N$ , $\alpha \in \ns ^*$ и $\beta \in \ns ^*$ множество P содержит правила 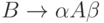$B \tto \alpha A \beta$ и $A \tto \varepsilon$ , но не содержит правила $B \tto \alpha \beta$ , то добавим это правило в P. Повторяем эту процедуру, пока возможно.

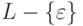Теперь исключим из множества P все правила вида $A \tto \varepsilon$ . Полученная грамматика порождает язык $L \sminus \{ \varepsilon \}$ .

Пример 8.2.2. Рассмотрим язык L, порождаемый грамматикой

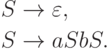
$\begin{align*} S \; & {\to} \; \varepsilon , \\ S \; & {\to} \; aSbS . \end{align*}$

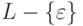Язык $L \sminus \{ \varepsilon \}$ порождается грамматикой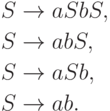

$\begin{align*} S \; & {\to} \; aSbS , \\ S \; & {\to} \; abS , \\ S \; & {\to} \; aSb , \\ S \; & {\to} \; ab . \end{align*}$

Упражнение 8.2.3. Найти контекстно-свободную грамматику без $\varepsilon$ -правил, эквивалентную грамматике

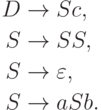
$\begin{align*} D \; & {\to} \; S c , \\ S \; & {\to} \; S S , \\ S \; & {\to} \; \varepsilon , \\ S \; & {\to} \; a S b . \end{align*}$

8.3. Нормальная форма Хомского

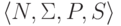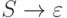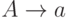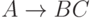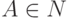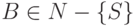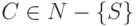Определение 8.3.1. Грамматика в нормальной форме Хомского ( грамматика в бинарной нормальной форме, квадратичная грамматика, grammar in Chomsky normal form) - контекстно-свободная грамматика $\lalg N , \Sigma , P , S \ralg$ , в которой каждое правило имеет один из следующих трех видов: $S \tto \varepsilon$ , $A \tto a$ , $A \tto B C$ , где $A \in N$ , $B \in N \sminus \{ S \}$ , $C \in N \sminus \{ S \}$ , $a \in \Sigma$ .

Пример 8.3.2. Грамматика

$\begin{align*} S \; & {\to} \; RR , & A \; & {\to} \; a , \\ S \; & {\to} \; AB , & B \; & {\to} \; RB , \\ R \; & {\to} \; RR , & B \; & {\to} \; b \\ R \; & {\to} \; AB , \end{align*}$

является грамматикой в нормальной форме Хомского.

Теорема 8.3.3. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Хомского.

Доказательство. Пусть дана контекстно-свободная грамматика 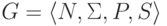$G = \lalg N , \Sigma , P , S \ralg$ . Проведем ряд преобразований этой грамматики так, что порождаемый ею язык остается неизменным.

Если правая часть какого-нибудь правила содержит символ S, то заменим грамматику 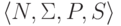$\lalg N , \Sigma , P , S \ralg$ на грамматику

$\lalg N \cup \{ S_0 \} , \Sigma , P \cup \{ S_0 \tto S \} , S_0 \ralg ,$

где S₀ - новый символ, не принадлежащий множеству $N \cup \Sigma$ .

Заменим во всех правилах каждый терминальный символ a на новый нетерминальный символ T_a и добавим к множеству P правила 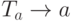$T_a \tto a$ для всех $a \in \Sigma$ .

Устраним правила вида $A \tto \alpha$ , где $| \alpha | > 2$ , заменив каждое из них на ряд более коротких правил (при этом добавляются новые нетерминальные символы).

Теперь устраним все правила вида $A \tto \varepsilon$ , где A не является начальным символом. Это можно сделать так же, как в доказательстве теоремы 8.2.1.

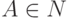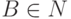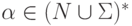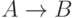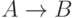Если для каких-то $A \in N$ , $B \in N$ и $\alpha \in \ns ^*$ множество P содержит правила $A \tto B$ и $B \tto \alpha$ , но не содержит правила $A \tto \alpha$ , то добавим это правило в P. Повторяем эту процедуру, пока возможно. После этого исключим из множества P все правила вида $A \tto B$ .

Пример 8.3.4. Грамматика

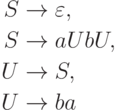
$\begin{align*} S \; & {\to} \; \varepsilon , \\ S \; & {\to} \; aUbU , \\ U \; & {\to} \; S , \\ U \; & {\to} \; ba \end{align*}$

эквивалентна следующей грамматике в нормальной форме Хомского:

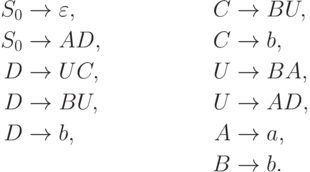
$\begin{align*} S_0 \; & {\to} \; \varepsilon , & C \; & {\to} \; BU , \\ S_0 \; & {\to} \; AD , & C \; & {\to} \; b , \\ D \; & {\to} \; UC , & U \; & {\to} \; BA , \\ D \; & {\to} \; BU , & U \; & {\to} \; AD , \\ D \; & {\to} \; b , & A \; & {\to} \; a , \\ & & B \; & {\to} \; b . \end{align*}$

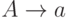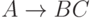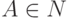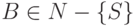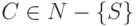Теорема 8.3.5. Если контекстно-свободный язык не содержит пустого слова, то он порождается некоторой грамматикой, в которой каждое правило имеет один из следующих двух видов: $A \tto a$ , $A \tto B C$ , где $A \in N$ , $B \in N \sminus \{ S \}$ , $C \in N \sminus \{ S \}$ , $a \in \Sigma$ .

Упражнение 8.3.6. Найти контекстно-свободную грамматику в нормальной форме Хомского, эквивалентную грамматике

$\begin{align*} F \; & {\to} \; ab , \\ F \; & {\to} \; a F b , \\ F \; & {\to} \; F F . \end{align*}$

Дальше >>

Авторизоваться

Математическая теория формальных языков

Нормальные формы контекстно-свободных грамматик

8.2. Устранение эпсилон-правил

8.3. Нормальная форма Хомского

Вопросы и ответы