Регулярные выражения

5.4*. Звездная высота

Определение 5.4.1. Звездная высота (star-height) регулярного выражения (обозначение sh(e) ) определяется рекурсивно следующим образом:

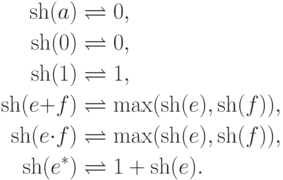
Пример 5.4.2. Пусть 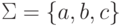. Тогда

sh((a*+b*+ab)*+(ab*c)*)  = 2.

Определение 5.4.3. Звездной высотой регулярного языка L (обозначение sh(L) ) называется минимум звездных высот регулярных выражений, задающих этот язык.

Замечание 5.4.4. Регулярный язык L является конечным тогда и только тогда, когда sh(L) = 0.

Теорема 5.4.5. Пусть 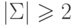. Тогда для любого 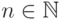существует такой регулярный язык , что sh(L) = n.

Доказательство можно найти в книге Саломаа А. Жемчужины теории формальных языков. - М.: Мир, 1986 с.41-46.

Пример 5.4.6. Пусть 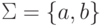и

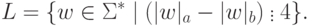
Замечание 5.4.7. Неизвестно, верен ли аналог теоремы 5.4.5 для обобщенных регулярных выражений, в которых, помимо итерации, конкатенации и объединения, разрешена операция дополнения.

Упражнение 5.4.8.Уменьшить звездную высоту регулярного выражения (a^*+b^*+ab)^*.

Упражнение 5.4.9.Уменьшить звездную высоту регулярного выражения (c(a^*b)^*)^*.

Упражнение 5.4.10.Уменьшить звездную высоту регулярного выражения (a(ab)^*b)^*.

Упражнение 5.4.11. Существует ли такой регулярный язык 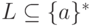, что sh(L) = 2?