НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 6: Регулярные выражения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.3. Теорема Клини

Определение 5.3.1. Назовем обобщенным конечным автоматом аналог конечного автомата, где переходы помечены не словами, а регулярными выражениями. Метка пути такого автомата - произведение регулярных выражений на переходах данного пути. Слово w допускается обобщенным конечным автоматом, если оно принадлежит языку, задаваемому меткой некоторого успешного пути.

Замечание 5.3.2. Каждый конечный автомат можно преобразовать в обобщенный конечный автомат, допускающий те же слова. Для этого достаточно заменить всюду в метках переходов пустое слово на 1, а каждое непустое слово - на произведение его букв.

Замечание 5.3.3. Если к обобщенному конечному автомату добавить переход с меткой 0, то множество допускаемых этим автоматом слов не изменится.

Пример 5.3.4. Пусть 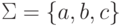$\Sigma = \{ a , b , c \}$ . Обобщенный конечный автомат $\lalg Q , \Sigma , \Delta , I , F \ralg$ , где Q = {1,2,3}, I = {1,2}, F = {3},

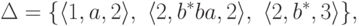
$\Delta = \{ \lp 1 , a , 2 \rp ,\ \lp 2 , b^* ba , 2 \rp ,\ \lp 2 , b^* , 3 \rp \} ,$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "2,1" _{a} & \\ *=[o][F-]{2} \ar @`{+/l16mm/} [] ^{} \ar "2,2" _{b^*} \rloop{0,-1} ^{b^*ba} & *=[o][F=]{3} }$

допускает все слова в алфавите $\Sigma$ , кроме слов, содержащих подслово aa.

Теорема 5.3.5 (теорема Клини). Язык L является регулярным тогда и только тогда, когда он является автоматным.

Доказательство. Пусть e - регулярное выражение. Индукцией по построению e легко показать, что задаваемый им язык является автоматным (см. теорему 3.1.1).

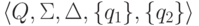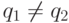Обратно, пусть язык L распознается некоторым (недетерминированным) конечным автоматом с одним начальным состоянием и одним заключительным состоянием. Существует эквивалентный ему обобщенный конечный автомат $\lalg Q , \Sigma , \Delta , \{ q_1 \} , \{ q_2 \} \ralg$ , где $q_1 \neq q_2$ . Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными ), заменим их на один переход, используя операцию +.

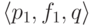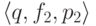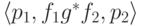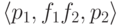Устраним по очереди все состояния, кроме q₁ и q₂. При устранении состояния q нужно для каждого перехода вида $\lp p_1 , f_1 , q \rp$ , где $p_1 \neq q$ , и для каждого перехода вида $\lp q , f_2 , p_2 \rp$ , где $p_2 \neq q$ , добавить переход $\lp p_1 , f_1 g^* f_2 , p_2 \rp$ , где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход $\lp p_1 , f_1 f_2 , p_2 \rp$ ), и снова всюду заменить параллельные переходы на один переход, используя операцию +.

После устранения всех состояний, кроме q₁ и q₂, получится обобщенный конечный автомат 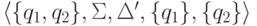$\lalg \{ q_1 , q_2 \} , \Sigma , \Delta' , \{ q_1 \} , \{ q_2 \} \ralg$ , где

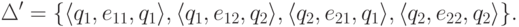
$\Delta' = \{ \lp q_1 , e_{11} , q_1 \rp , \lp q_1 , e_{12} , q_2 \rp , \lp q_2 , e_{21} , q_1 \rp , \lp q_2 , e_{22} , q_2 \rp \} .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{e_{11}} \ar "1,2" <0.6mm> ^{e_{12}} & *=[o][F=]{q_2} \ar "1,1" <0.6mm> ^{e_{21}} \rloop{0,1} ^{e_{22}} }$

Очевидно, что $L = \regval{ e_{11}^* e_{12} ( e_{22} \replus e_{21} e_{11}^* e_{12} )^* }$ .

Пример 5.3.6. Рассмотрим язык, распознаваемый конечным автоматом

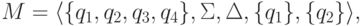
$M = \lalg \{ q_1 , q_2 , q_3 , q_4 \} , \Sigma , \Delta , \{ q_1 \} , \{ q_2 \} \ralg ,$

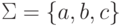где $\Sigma = \{ a , b , c \}$ и

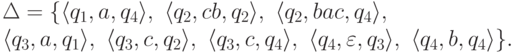
$\begin{multiline*} \Delta = \{ \lp q_1 , a , q_4 \rp ,\ \lp q_2 , cb , q_2 \rp ,\ \lp q_2 , bac , q_4 \rp ,\ \\ \lp q_3 , a , q_1 \rp ,\ \lp q_3 , c , q_2 \rp ,\ \lp q_3 , c , q_4 \rp ,\ \lp q_4 , \varepsilon , q_3 \rp ,\ \lp q_4 , b , q_4 \rp \} . \end{multiline*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{a} & *=[o][F-]{q_4} \ar "2,2" <0.6mm> ^{\varepsilon} \rloop{0,1} ^{b} & *=[o][F=]{q_2} \rloop{0,1} ^{cb} \ar "1,2" _{bac} \\ % & *=[o][F-]{q_3} \ar "1,1" ^{a} \ar "1,3" _{c} \ar "1,2" <0.6mm> ^{c} & }$

Тот же язык порождается обобщенным конечным автоматом

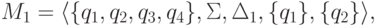
$M_1 \peq \lalg \{ q_1 , q_2 , q_3 , q_4 \} , \Sigma , \Delta_1 , \{ q_1 \} , \{ q_2 \} \ralg ,$

где

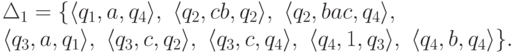
$\begin{multiline*} \Delta_1 = \{ \lp q_1 , a , q_4 \rp ,\ \lp q_2 , cb , q_2 \rp ,\ \lp q_2 , bac , q_4 \rp ,\ \\ \lp q_3 , a , q_1 \rp ,\ \lp q_3 , c , q_2 \rp ,\ \lp q_3 , c , q_4 \rp ,\ \lp q_4 , 1 , q_3 \rp ,\ \lp q_4 , b , q_4 \rp \} . \end{multiline*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{a} & *=[o][F-]{q_4} \ar "2,2" <0.6mm> ^{1} \rloop{0,1} ^{b} & *=[o][F=]{q_2} \rloop{0,1} ^{cb} \ar "1,2" _{bac} \\ % & *=[o][F-]{q_3} \ar "1,1" ^{a} \ar "1,3" _{c} \ar "1,2" <0.6mm> ^{c} & }$

После устранения состояния q₃ получается обобщенный конечный автомат

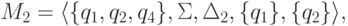
$M_2 = \lalg \{ q_1 , q_2 , q_4 \} , \Sigma , \Delta_2 , \{ q_1 \} , \{ q_2 \} \ralg ,$

где

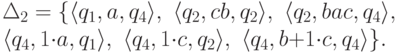
$\begin{multiline*} \Delta_2 = \{ \lp q_1 , a , q_4 \rp ,\ \lp q_2 , cb , q_2 \rp ,\ \lp q_2 , bac , q_4 \rp ,\ \\ \lp q_4 , 1 \redot a , q_1 \rp ,\ \lp q_4 , 1 \redot c , q_2 \rp ,\ \lp q_4 , b \replus 1 \redot c , q_4 \rp \} . \end{multiline*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix @=11mm{ *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" <0.6mm> ^{a} & *=[o][F-]{q_4} \ar "1,1" <0.6mm> ^{1 \cdot a} \ar "1,3" <0.6mm> ^{1 \cdot c} \rloop{0,1} ^{b + 1 \cdot c} & *=[o][F=]{q_2} \rloop{0,1} ^{cb} \ar "1,2" <0.6mm> ^{bac} }$

Можно упростить регулярные выражения и получить

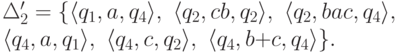
$\begin{multiline*} \Delta_2' = \{ \lp q_1 , a , q_4 \rp ,\ \lp q_2 , cb , q_2 \rp ,\ \lp q_2 , bac , q_4 \rp ,\ \\ \lp q_4 , a , q_1 \rp ,\ \lp q_4 , c , q_2 \rp ,\ \lp q_4 , b \replus c , q_4 \rp \} . \end{multiline*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix @=11mm{ *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" <0.6mm> ^{a} & *=[o][F-]{q_4} \ar "1,1" <0.6mm> ^{a} \ar "1,3" <0.6mm> ^{c} \rloop{0,1} ^{b + c} & *=[o][F=]{q_2} \rloop{0,1} ^{cb} \ar "1,2" <0.6mm> ^{bac} }$

После устранения состояния q₄ и упрощения регулярных выражений получается обобщенный конечный автомат

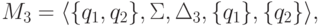
$M_3 = \lalg \{ q_1 , q_2 \} , \Sigma , \Delta_3 , \{ q_1 \} , \{ q_2 \} \ralg ,$

где

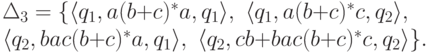
$\begin{multiline*} \Delta_3 = \{ \lp q_1 , a ( b \replus c )^* a , q_1 \rp ,\ \lp q_1 , a ( b \replus c )^* c , q_2 \rp ,\ \\ \lp q_2 , bac ( b \replus c )^* a , q_1 \rp ,\ \lp q_2 , cb \replus bac ( b \replus c )^* c , q_2 \rp \} . \end{multiline*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix @=11mm{ *=[o][F-]{q_1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{a (b+c)^* a} \ar "1,3" <0.6mm> ^{a (b+c)^* c} & & *=[o][F=]{q_2} \ar "1,1" <0.6mm> ^{bac (b+c)^* a} \rloop{0,1} ^{cb + bac (b+c)^* c} }$

Следовательно, язык L(M) задается регулярным выражением

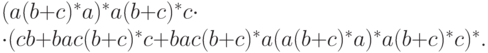
$\begin{multiline*} ( a ( b \replus c )^* a )^* a ( b \replus c )^* c \redot \\ \redot ( cb \replus bac ( b \replus c )^* c \replus bac ( b \replus c )^* a ( a ( b \replus c )^* a )^* a ( b \replus c )^* c )^* . \end{multiline*}$

Упростив это регулярное выражение, получим

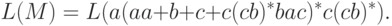
$L ( M ) = \regval{ a ( aa \replus b \replus c \replus c (cb)^* bac)^* c (cb)^* } .$

Упражнение 5.3.7. Найти регулярное выражение для языка, порождаемого грамматикой

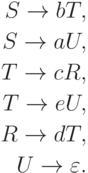
$\begin{align*} \regl{ S \tto b T } \regl{ S \tto a U } \regl{ T \tto c R } \regl{ T \tto e U } \regl{ R \tto d T } \regl{ U \tto \varepsilon }. \end{align*}$

Упражнение 5.3.8. Найти регулярное выражение для языка 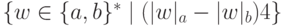$\{ w \in \{a,b\}^* \mid ( | w |_a - | w |_b ) \Vdots 4 \}$

Упражнение 5.3.9. Найти регулярное выражение для языка 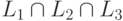$L_1 \cap L_2 \cap L_3$ , где L₁ = (aaab+c+d)^*, L₂ = (a^*ba^*ba^*bc+d)^*, L₃ = ((a+b)^*c(a+b)^*cd)^*

Упражнение 5.3.10 Найти регулярное выражение для дополнения языка (a+b)^*bbb(a+b)^* в алфавите {a,b}.

Упражнение 5.3.11 Найти регулярное выражение для дополнения языка (ab+ba)^*(1+a+b) в алфавите {a,b}.

Упражнение 5.3.12 Найти регулярное выражение для дополнения языка (a+b)^*(aab+abaa+abb)(a+b)^* в алфавите {a,b}.

Упражнение 5.3.13 Найти регулярное выражение для дополнения языка (aa(ab)^*bb(ab)^*)^* в алфавите {a,b}.

Дальше >>

Авторизоваться

Математическая теория формальных языков

Регулярные выражения

5.3. Теорема Клини

Вопросы и ответы