Проективная геометрия в компьютерном зрении

1.3 Модель искажений линз

Мы рассмотрели хорошую математическую модель, которая работает в идеальном случае. Но это еще не все, что нам нужно. На практике у нас возникают дополнительные эффекты из-за того, что мир неидеальный, и линзы они тоже несовершенны – они вносят свои искажения. Например, вы видите то, что в трехмерном мире было прямой линией на изображении перешло в некую изогнутую кривую.

Рис. 5.7. Fisheye lens room (Wikimedia)

На самом деле, в предыдущей математической модели прямые линии должны переходят в прямые. На приведенном рисунке искажения вносят непосредственно линзы. Их тоже нужно моделировать для того чтобы корректно предсказывать, как трехмерный мир перейдет на изображение. Для того чтобы это моделировать вводятся так называемые коэффициенты дисторсии и рассматривается довольно сложная модель:

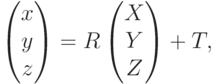
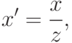
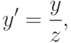
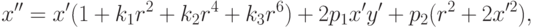
где

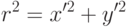
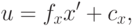
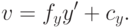
Отметим только, что все эти искажения мы приближаем неким полиномом. У этого полинома есть некоторые коэффициенты – это и есть коэффициенты дисторсии, которые моделируют искажения. Если мы сможем для камеры посчитать эти коэффициенты, то, тем самым, мы сможем предсказать, какие искажения вносит эта камера. В этом случае, зная трехмерный мир, зная проекционную матрицу камеры и коэффициенты дисторсии, мы можем корректно предсказать, куда именно спроецируется трехмерная точка на изображение. Идея в том, что вместо идеальной проективной проекции произойдет переход в какое-то искаженное положение, которое мы должны здесь учесть.

1.4. Определение позы объекта. Задача PnP.

Теперь рассмотрим конкретный пример того, как описанную модель камеры можно использовать для получения каких-нибудь знаний о трехмерном мире по его изображению. Сейчас мы попытаемся найти позу объекта. Это как раз задача из примера с роботом: чтобы взять объект, робот должен понять, как именно объект расположен в трехмерном мире. Мы рассмотрим, как эту задачу можно решать.

Объект изначально имеет некие трехмерные точки в какой-то системе координат, связанной с объектом (не так важно какую именно систему координат брать). Также мы знаем координаты точек объекта на изображении, и мы знаем, что эта точка изображения соответствует конкретной трехмерной точке. Как этого добиться и как найти такие соответствия – об этом вам должны были рассказывать в лекции про детекторы и дескрипторы. Это как раз стандартный способ нахождения таких соответствий. Если вы знаете дескрипторы, которые возможны для трехмерной точки, то вы сможете найти соответствие этих дескрипторов с точкой на изображении. И, таким образом, понять, что вот эта трехмерная точка соответствует именно вот этой двухмерной точке. То есть если это какая-то специфическая точка на объекте, с характерной текстурой, то такое соответствие вы сможете построить. Когда есть такие соответствия из 3d в 2d, мы можем поставить задачу поиска объекта. Нам нужно определить позу объекта – то есть найти конкретные матрицы R и T, которые характеризуют позу объекта. Например, если цилиндр расположен в той же ориентации, что и изначально, то у него будет просто какой-то вектор переноса. Если он еще повернут, то соответственно будет еще какая-то матрица поворота. Это и будет поза объекта, которая нужна роботу, чтобы его взять.

Для того чтобы эту задачу решать, мы можем на нее посмотреть как на задачу оптимизации. Что мы хотим сделать? У нас есть трехмерные точки, мы знаем, что для проекционной матрицы P точки (X,Y,Z) проецируются в некие (u,v) при какой-то фиксированной позе R,T . И мы хотим взять такие R и T , чтобы вот эти проекции совпадали с теми координатами, которые мы на самом деле наблюдаем. Мы хотим, чтобы точка объекта спроецировалась именно в соответствующую точку на изображении. Таким образом, получаем задачу оптимизации: необходимо найти минимум функции ошибки

варьируя R и T , при условиях

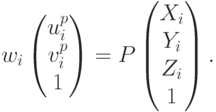
Вообще говоря, можно рассматривать не только такую целевую функцию для минимизации; можно было бы рассматривать какие-то другие функции и соответственно получалось бы другое решение. Например, можно рассматривать ошибку не в плоскости изображения, а в трехмерном мире:

Рис. 5.8.

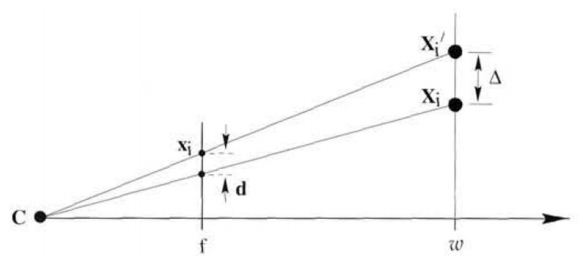
– у нас есть камера C, оптическая ось и плоскость изображения, на которую мы проецируем. Раньше она у нас была сзади – за камерой – но мы ее можем перенести вперед, и это будет фактически тоже самое. Когда у нас изображение находилось сзади камеры – с этим было не очень удобно работать – так как все переворачивалось. Поэтому вводят виртуальную плоскость, расположенную перед камерой, тогда точка объекта, которая находилась вверху, будет и верхней точкой проекции. И это уже то, что постоянно используется, и с чем удобно работать. Соответственно, мы рассматриваем виртуальную плоскость (слайд 14), нам известна точка Xi на изображении – мы спроецировали нашу точку модели и мы можем рассматривать ошибку репроекции, то есть ошибку вот этого расстояния на изображении. Вообще говоря, можно было бы рассматривать расстояние в трехмерном пространстве – то есть точку модели и реальные трехмерные координаты. И соответственно рассматривать минимизацию такой целевой функции. Решение получилось бы немножко другое, потому что ошибка на изображении будет одинаковой (у точек общая проекция), а в трехмерном пространстве, если мы их будем сдвигать – геометрическое расстояние в трехмерном мире оно будет меняться. То есть можно рассматривать и другие целевые функции – будет своя ошибка, которую мы будем минимизировать:

То, что мы здесь обсудили, называется проблемой PnP (perspective- -points problem): у нас есть трехмерные точки, у нас есть двумерные соответствия и внутренние параметры камеры. Проблема заключается в поиске позы объекта R,T.

Рассмотрим один из самых простых способов ее решения – метод DLT (Direct Linear Transformation). Идея метода очень красивая. Мы хотим, чтобы трехмерные точки проецировались в известные точки на изображении:

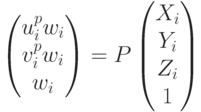
Из-за однородных координат у нас получается коэффициент w. В правой части записан трехмерной вектор, и в левой части записан трехмерный вектор, которому соответствует целая прямая. Мы хотим, чтобы при правильно подобранном , они бы совпали. Но поскольку непонятно, откуда этот брать, то мы можем задачу решать по-другому – мы можем сказать, что эти векторы должны быть коллинеарны и поэтому векторное произведение этих векторов должно быть равно нулю:

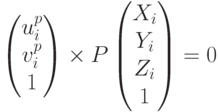
Таким образом, мы получаем уравнение относительно матрицы P, которое мы уже можем решать – получается просто система линейных уравнений. Тем самым мы найдем позу объекта. Метод получается очень простой, но тем не менее, есть другие методы, потому что, когда мы будем решать систему линейных уравнений, то у нас будет минимизироваться вектор невязки – сумма квадратов ошибок в этой системе – то есть мы минимизируем некую алгебраическую ошибку – каков ее физический смысл – так сразу и непонятно. На выходе мы что-то получим, но что именно мы минимизировали проинтерпретировать физически сложно. Поэтому методы, которые явно минимизируют ошибку репроекции в этом отношении лучше, потому что мы четко понимаем, что мы минимизируем, и наша целевая функция действительно осмысленная. Обычно используются именно такие методы, но в явном виде решение в них не выведешь, поэтому используются оптимизационные методы. Например, метод Левенберга-Марквардта, который представляет собой смесь градиентного спуска и метода Ньютона, в нем динамически определяются, какой алгоритм лучше использовать. Есть другие методы, которые используют три соответствия или четыре соответствия и находят позу. Вообще говоря, для того чтобы решить задачу PnP нужно как минимум четыре соответствия для того, чтобы не было неоднозначности. На практике обычно берется больше соответствий для того чтобы убрать влияние шумов и получить точную оценку. Есть очень важный момент, о котором мы сейчас поговорим – то, что в этих соответствиях очень часто бывают шумы. Если вы помните из детекторов-дескрипторов – когда мы находим соответствия – то у нас не вот идеально находится один дескриптор и соответствующий ему второй дескриптор – часто возникают ложные соответствия. И поэтому в том методе, который мы обсудили – ничего работать не будет, потому что мы будем пытаться минимизировать ошибку репроекции там, где вообще у нас что-то проецируется совсем не туда. Поэтому хорошего результата мы не получим. Для работы с большим количеством ложных соответствий используется метод RANSAC. Это очень популярная идея, которая используется в большом количестве задач.

Идея состоит в том, что мы не можем оптимизировать по всем соответствиям сразу из-за наличия шумов – поэтому мы выберем 4 случайных соответствия – что позволит однозначно определить позу. И так мы будем делать много-много раз. В какой-то момент нам повезет – мы выберем такие 4 соответствия, что все они правильные. По этим 4 соответствиям мы оценим правильную позу. И чтобы понять, что найденная поза действительно правильная мы делаем следующее – рассчитаем количество так называемых инлайеров. Что такое инлайер? Вот у нас есть трехмерные точки, мы нашли некоторую позу R и T, и для этих точек применяет эту позу и смотрим, перешли ли они в соответствующие точки. Если точки спроецировались близко – то это намек на то, что поза правильная. Одно соответствие сработало – трехмерная точка перешла в правильную двумерную. Соответственно, если большое количество точек при найденной позе переходит в правильные точки, то мы почти уверены, что поза правильная. Можно добавить еще один шаг. После того как мы нашли лучшее преобразование, которое дает максимальное количество инлайеров, мы уточняем его по всем найденным соответствиям. Мы позу изначально нашли по 4 соответствиям, теперь, когда мы уже знаем, какие соответствия правильные, а какие нет, мы посчитаем позу по всем соответствиям. Как долго работает этот алгоритм? Нужно делать много итераций, но каждая итерация довольно простая. Выборка случайных точек – это просто; найти преобразование по 4 точкам – это тоже просто; с нахождением количества инлайеров ситуация уже посложнее, потому что нам нужно взять все трехмерные точки, спроецировать их, проверить перешли ли они в соответствующие, но все равно это не очень тяжелая операция.

Рассмотрим еще один пример, чтобы лучше прочувствовать метод RANSAC: как можно применять этот метод к поиску прямых. У нас есть двумерные точки, где-то в них есть какая-то прямая, но при этом есть очень много разных шумов. Прямая угадывается, на ней очень много точек. Но как нам найти такую прямую? Если мы стандартно попытается применить метод наименьших квадратов –то понятно, что ничего хорошего не будет, шумы нам все испортят. Поэтому здесь можно применять метод RANSAC. Мы случайно берем две точки, проводим прямую и смотрим, сколько получилось инлайеров – то есть, сколько точек попало на эту прямую. Сейчас мы очень неудачно выбрали точки – на этой прямой точек почти нет. Если на следующей итерации мы возьмем другие две точки, то одна точка на нее попала, и у нас есть три точки на прямой. Так мы будем делать много-много раз, и в какой-то момент нам повезет, мы выберем точки, которые действительно лежат на прямой. У нас будет очень много инлайеров, и очень много точек лежат близко к этой прямой.

Давайте обсудим, сколько нам нужно итераций для того, чтобы все получилось хорошо. Здесь все зависит от того, насколько много у нас ложных соответствий и насколько много правильных. Если бы у нас все соответствия были правильные, то мы бы сошлись за одну итерацию. Если же у нас много ложных соответствий, то нам понадобится много итераций для того чтобы найти правильное. Если вероятность выбрать правильное соответствие равна p, например, 0.2, если у нас 20% соответствий правильные. Для того чтобы метод нашел правильную модель – правильную прямую или правильную позу – нам нужно чтобы все соответствия были правильными – то есть нам нужно выбрать k соответствий правильных. Грубо говоря, это будет 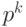– вероятность того, что все k соответствий правильные. И если найти теперь мат. ожидание. Сколько нам нужно сделать итераций n, чтобы событие с вероятностью pk наступило? Легко выводится, что мат. ожидание количества операций будет обратное – 1/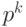 . То есть если у нас 50% соответствий правильные, и нам нужно найти 4 соответствия, то нам понадобится 1/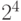 итераций, то есть не так уж и много. Формулу вы можете видеть на слайде 18.

Рассмотрим конкретный пример. Задача для робота – задача определения позы объекта.

Рис. 5.9.

Вот у нас объекты были в тренировочном глазе, робот обучился, запомнил их, и теперь, когда ему пришла новая картинка, где он хочет понять, где какие объекты расположены, то это можно сделать, именно решая задачу PnP. Мы находим соответствия, используя дескрипторы, потом запускаем схему RANSAC, и находим позу для каждого из объектов.