|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
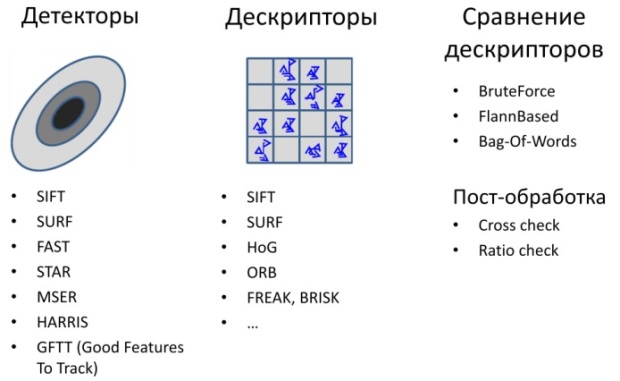
Начало работы с библиотекой OpenCV
1.4.3. Пример: поиск плоских объектов
В качестве практического примера использования OpenCV c С++ рассмотрим задачу поиска на изображении плоских объектов. Пусть имеется некоторое изображение плоского объекта, например, передняя грань коробки. Требуется найти этот объект на другом большом изображении некоторой сложной сцены. Коробка может быть загорожена другими объектами, ориентирована произвольным образом в пространстве. Освещение сцены может быть иным.
Основная идея метода – нахождение особых точек, т. е. точек, примечательных для данного объекта, за которые можно "зацепиться". Однородные участки поверхности для идентификации объекта обычно не подходят, так как могут совпасть с чем угодно. Если возьмем окрестность более интересных точек – то случайное совпадение маловероятно. Мы находим точки, строим их описание (дескрипторы), и пытаемся найти похожие точки на втором изображение. После чего отфильтровываем неправильно сопоставленные точки, исходя из гипотезы что объект жесткий (недеформируемый) и поэтому все точки на нем должны преобразовываться от одного кадра к другому согласованно. В случае плоского объекта это должно быть перспективное преобразование (гомография).
Все необходимое для реализации этого метода есть в модуле features2d. Он позволяет находить особые точки, строить их дескрипторы, применять методы сравнения дескрипторов.
Приведем код, решающий данную задачу:
// Загружаем изображения:
Mat img1 = imread(argv[1], CV_LOAD_IMAGE_GRAYSCALE);
Mat img2 = imread(argv[2], CV_LOAD_IMAGE_GRAYSCALE);
// Находим особые точки на каждом изображении
// Вычисляем их дескрипторы:
Ptr<Feature2D>
surf=Algorithm::create<Feature2D>("Feature2D.SURF");
vector<KeyPoint> keypoints1, keypoints2;
Mat descriptors1, descriptors2;
surf->operator()(img1, Mat(), keypoints1, descriptors1);
surf->operator()(img2, Mat(), keypoints2, descriptors2);
// Находим наилучшее соответствие между особыми точками
// на изображениях
vector<DMatch> matches;
BFMatcher(NORM_L2, true).match(descriptors1, descriptors2,
matches);
// Находим оптимальное преобразование,
// согласующееся с большинством пар точек.
vector<Point2f> pt1, pt2;
for( size_t i = 0; i < matches.size(); i++ ) {
pt1.push_back(keypoints1[matches[i].queryIdx].pt);
pt2.push_back(keypoints2[matches[i].trainIdx].pt);
}
// H – это матрица оптимального перспективного
// преобразования от img1 к img2
Mat H = findHomography(pt1, pt2, RANSAC, 10);
Мы загружаем оба изображения. Находим особые точки и вычисляем их дескрипторы. При этом создаем экземпляр алгоритма Feature2D, используя параметры по умолчанию. В результате получаем 2 "списка" особых точек и 2 "списка" их дескрипторов: keypoints1, keypoints2, descriptors2, descriptors2, при этом keypoints1, keypoints2 – это векторы, содержащие номера особых точек, а descriptors2, descriptors2 – матрицы, строки которых содержат их дескрипторы.
На рисунке указаны найденные особые точки.
После этого, сравнивая каждый набор дескрипторов из первого изображения, с каждым таким набором из второго изображения, находим наилучшее соответствие между особыми точками.
На рисунке графически изображено найденное соответствие.
Далее находим матрицу наилучшего перспективного преобразования (гомографии), осуществляющую это соответствие.
На рисунке отмечены "правильные" пары особых точек, т. е. пары, подчиняющиеся найденному перспективному преобразованию. Обратите внимание на пару точек (самый верхний отрезок), найденную ошибочно (эти точки принадлежат разным объектам), но геометрически не противоречащую остальным парам.
После того как матрица гомографии найдена само расположение коробки в пространтсве можно найти с помощью функции solvePnP().
Заметим, что данный метод работает также для склейки панорам, если снимаемая сцена (например пейзаж) находится достаточно далеко от точки съемки, чтобы считать ее плоской.
В случае неплоских объектов, "правильные" пары можно найти с помощью findFundamentalMat() вместо findHomography(), после чего опять использовать solvePnP().