|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Детекторы и дескрипторы ключевых точек. Алгоритмы классификации изображений. Задача детектирования объектов на изображениях и методы её решения
3. Задача классификации изображений и методы еe решения
3.1. Алгоритмы класса bag-of-words
К одному из наиболее распространенных классов алгоритмов классификации изображений можно отнести так называемые bag-of-words (также известные как bag-of-features или bag-of-keypoints) методы, впервые предложенные в работе [ 27 ]. Фактически bag-of-words использует в качестве описания гистограмму вхождений отдельных шаблонов в изображение. Корни идеи восходят к задаче классификации текстов, для решения которой используют описания в виде гистограмм вхождений в документ слов из заранее составленного словаря.
Корни идеи восходят к задаче классификации текстов, для решения которой используют описания в виде гистограмм вхождений в документ слов из заранее составленного словаря.
Основные шаги алгоритмов класса bag-of-words могут быть описаны следующим образом:
- Детектирование ключевых точек на изображении
- Построение описания (дескрипторов) локальных окрестностей ключевых точек
- Кластеризация дескрипторов ключевых точек, принадлежащих всем объектам обучающей выборки (это соответствует построению словаря, "словами" в котором являются центроиды построенных кластеров)
- Построение описания каждого изображения в виде нормированной гистограммы встречаемости "слов" (для каждого кластера вычисляется количество отнесенных к нему ключевых точек, принадлежащих определенному изображению)
- Построение классификатора, использующего вычисленное на шаге 4 признаковое описание изображения.
На дескрипторы, используемые алгоритмами данного класса, накладываются определенные ограничения: в частности, они должны быть инварианты к аффинным преобразованиям изображения, изменениям в условиях освещенности и окклюзиям. Словарь дескрипторов ключевых точек должен быть достаточно большим, чтобы отражать релевантные изменения частей изображения, но в то же время не чрезмерным, чтобы сделать алгоритм устойчивым к шуму.
Одним из недостатков классического bag-of-words подхода является то, что он никак не учитывает пространственную информацию о распределении ключевых точек на изображении. Это приводит к тому, что описания объектов со схожими по дескрипторам наборами ключевых точек, находящимися в совершенно разных конфигурациях, совпадают. Для того чтобы учесть пространственную информацию, было предложено несколько подходов. Так, в работе [ 143 ] используются т.н. кореллограммы визуальных слов, позволяющие эффективно моделировать типовые пространственные корреляции между визуальными словами для определенных классов. В работе [ 144 ] рассматривается двухуровневая иерархическая модель, в которой объект представляется  частями, к каждой из которых относится
частями, к каждой из которых относится 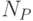 ключевых точек. Широкое развитие получил подход, в котором используется сопоставление пространственных пирамид признаков (де-факто, объект описывается не одной гистограммой, а объединением гистограмм, соответствующих отдельным частям изображения). Подробное изложение подхода приведено в разделе 3.2.
ключевых точек. Широкое развитие получил подход, в котором используется сопоставление пространственных пирамид признаков (де-факто, объект описывается не одной гистограммой, а объединением гистограмм, соответствующих отдельным частям изображения). Подробное изложение подхода приведено в разделе 3.2.
3.2. Сопоставление пространственных пирамид
Пусть X и Y – два множества векторов в d-мерном пространстве признаков (данные множества векторов соответствуют наборам дескрипторов ключевых точек). В работе [ 52 ] предложена схему сопоставления пирамид, которая находит приблизительное соответствие между двумя множествами такого типа. Данный алгоритм работает следующим образом: пространство признаков разбивается на последовательность вложенных друг в друга подобластей (ячеек) и вычисляется взвешенная сумма числа совпадений на всех уровнях разбиения. Для каждого фиксированного уровня две точки считаются соответствующими, если они принадлежат одной подобласти, совпадения на более детальных уровнях разбиения учитываются с большим весом, чем соответствия, найденные на более грубых уровнях разбиения.
Пусть имеется  уровней разбиения
уровней разбиения 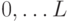 , где
, где  -ому уровню соответствует
-ому уровню соответствует 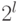 ячеек по каждой размерности (таким образом, общее число ячеек на
ячеек по каждой размерности (таким образом, общее число ячеек на  -ом уровне равно
-ом уровне равно  ). Пусть
). Пусть 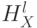 и
и 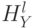 – гистограммы, описывающие множества
– гистограммы, описывающие множества  и
и  , в которых
, в которых 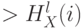 и
и 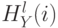 соответствует числу точек из
соответствует числу точек из  и
и  , которые относятся к
, которые относятся к  -ой ячейке. Тогда число совпадений на
-ой ячейке. Тогда число совпадений на  -ом уровне разбиения вычисляется с помощью функции пересечения гистограмм:
-ом уровне разбиения вычисляется с помощью функции пересечения гистограмм:

Необходимо отметить, что число совпадений, найденных на уровне  , также включает в себя число совпадений, найденных на уровне
, также включает в себя число совпадений, найденных на уровне  , поэтому число новых совпадений, найденных на уровне
, поэтому число новых совпадений, найденных на уровне  , вычисляется как
, вычисляется как 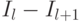 для всех
для всех  . Вес, соответствующий уровню
. Вес, соответствующий уровню  , устанавливается равным
, устанавливается равным  , что обратно пропорционально ширине ячейки на этом уровне. С практической точки зрения кажется целесообразным установить меньший вклад в итоговую функцию числа совпадений совпадения, найденные на более грубых уровнях разбиений, т.к. они включают в себя явно непохожие друг на друга признаки.
, что обратно пропорционально ширине ячейки на этом уровне. С практической точки зрения кажется целесообразным установить меньший вклад в итоговую функцию числа совпадений совпадения, найденные на более грубых уровнях разбиений, т.к. они включают в себя явно непохожие друг на друга признаки.
Суммируя функции пересечения гистограмм на всех уровнях, получаем функцию ядра сопоставления пирамид:

Очевидно, что приведенная выше схема работает с неупорядоченным представлением изображения (функции, описанной выше, не важно расположение ключевых точек внутри изображения). Это позволяет точно сопоставить 2 набора признаков в многомерном пространстве, игнорируя при этом всю пространственную информации об их расположении на изображении. Авторами схемы сопоставления пространственных пирамид в работе [ 67 ] предложен альтернативный подход: выполнять сопоставление пирамид в двухмерном пространстве и использовать алгоритмы кластеризации в пространстве признаков. Все вектора признаков квантизуются к  дискретным типам (что соответствует отнесению вектора признаков к одному из
дискретным типам (что соответствует отнесению вектора признаков к одному из  кластеров), и делается предположение, что только признаки одного типа могут соответствовать друг другу. Каждому значению
кластеров), и делается предположение, что только признаки одного типа могут соответствовать друг другу. Каждому значению 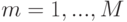 соответствует набор двухмерных векторов
соответствует набор двухмерных векторов 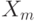 и
и 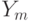 Ym, представляющих координаты векторов признаков типа m, найденных на изображении. Итоговая функция ядра сопоставления пирамид является суммой отдельных ядер для каждого типа признаков:
Ym, представляющих координаты векторов признаков типа m, найденных на изображении. Итоговая функция ядра сопоставления пирамид является суммой отдельных ядер для каждого типа признаков:

Так как функция ядра сопоставления пирамид является взвешенной суммой функций пересечения гистограмм, можно представить 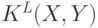 как единую функцию пересечения гистограмм для векторов признаков, полученных конкатенаций соответствующим образом взвешенных гистограмм, относящихся ко всем
как единую функцию пересечения гистограмм для векторов признаков, полученных конкатенаций соответствующим образом взвешенных гистограмм, относящихся ко всем  типам признаков и ко всем уровням пирамиды. Для
типам признаков и ко всем уровням пирамиды. Для  уровней и
уровней и  типов признаков результирующий вектор будет иметь размерность
типов признаков результирующий вектор будет иметь размерность 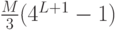 . Однако в силу разреженности гистограмм сложность вычисления ядра является линейной от числа признаков.
. Однако в силу разреженности гистограмм сложность вычисления ядра является линейной от числа признаков.
3.3. Модели объектов, основанные на частях
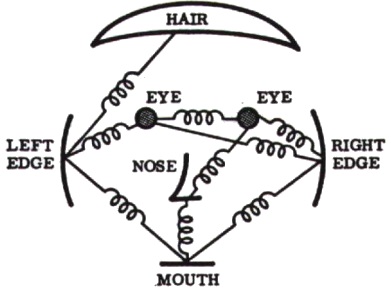
Одним из наиболее известных подходов к классификации объектов является использование моделей объектов, основанных на частях (part-based models). В отличие от bag-of-words методов с добавленной информацией о расположении ключевых точек алгоритмы данного класса явно учитывают взаимное расположение различных частей объекта. Впервые подход был представлен в работе [ 142 ] для задачи классификации лиц.
Основными элементами моделей объектов, основанных на частях, являются:
- представление (модель) отдельных частей объекта;
- методы обучения данного представления;
- описание связей между частями объекта.
Конфигурация, которой описывается взаимное расположение частей объекта, является одним из ключевых факторов, влияющих на качество и быстродействие для моделей данного класса. Если предположить, что объект содержит  частей, при этом для каждой части на изображении возможно
частей, при этом для каждой части на изображении возможно  различных положений, то в данном случае имеется
различных положений, то в данном случае имеется 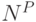 различных конфигураций, что накладывает ограничение на практическую применимость методов в силу вычислительной сложности (при сопоставлении частей классифицируемого изображения с частями обученной модели (т.н. вывода (inference)) приходится выполнить
различных конфигураций, что накладывает ограничение на практическую применимость методов в силу вычислительной сложности (при сопоставлении частей классифицируемого изображения с частями обученной модели (т.н. вывода (inference)) приходится выполнить 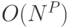 операций. Ряд используемых моделей представлено на рис. 3.5 [ 140 ]
операций. Ряд используемых моделей представлено на рис. 3.5 [ 140 ]
a) Constellation ("созвездие") [ 135 ] (вычислительная сложность вывода 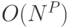 )
)
b) Star ("звезда") [ 134 ] (вычислительная сложность вывода 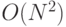 )
)
c) k-fan [ 136 ] (вычислительная сложность 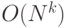 , где
, где  – число частей в клике графа, являющейся основой модифицированной структуры типа "звезда")
– число частей в клике графа, являющейся основой модифицированной структуры типа "звезда")
d) Tree ("дерево") [ 137 ] (вычислительная сложность вывода 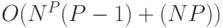 с при использовании основанного на динамическом программировании алгоритма Витерби [ 141 ])
с при использовании основанного на динамическом программировании алгоритма Витерби [ 141 ])
e) Bag-of-features [ 138 ]
f) Hierarchy (иерархическая структура, описывающая зависимость между частями объекта и их объединениями (укрупненными частями)) [ 139 ]
g) Sparse flexible models (направленный ациклический граф, описывающий отношение между частями объекта) [ 140 ]
Для представления отдельных частей объекта могут использоваться как дескрипторы ключевых точек (например, SIFT), так и другие признаки, например результаты PCA преобразования интенсивностей пикселей внутри патча, соответствующего части изображения, гистограммы ориентированных градиентов (HoG) [ 26 ] и т.д.
При обучении представления отдельных частей объекта используются как генеративные (например, Байесов классификатор), так и дискриминативные алгоритмы машинного обучения, которые отличаются лучшей точностью предсказания. В частности, в работе [ 39 ] был предложен подход, основанный на описании частей объекта в виде гистограмм ориентированных градиентов, для обучения представления отдельных частей используется скрытый метод опорных векторов (Latent SVM).