Самостоятельная работа 2: Оптимизация вычислительно трудоемкого программного модуля для архитектуры Intel Xeon Phi. Линейные сортировки
Чётно-нечетное слияние Бэтчера
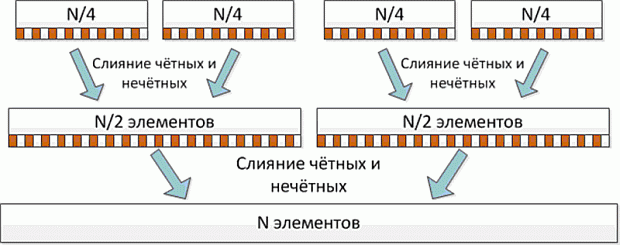
Чётно-нечётное слияние Бэтчера заключается в том, что два упорядоченных массива, которые необходимо слить, разделяются на чётные и нечётные элементы [ [ 4.3 ] ]. Такое слияние может быть выполнено параллельно. Чтобы массив стал окончательно отсортированным, достаточно сравнить пары элементов, стоящие на нечётной и чётной позициях. Первый и последний элементы массива проверять не надо, т.к. они являются минимальным и максимальным элементов массивов.
Чётно-нечётное слияние Бэтчера позволяет задействовать 2 потока при слиянии двух упорядоченных массивов. В этом случае слияние n массивов могут выполнять n параллельных потоков. На следующем шаге слияние n/2 полученных массивов будут выполнять n/2 потоков и т.д. На последнем шаге два массива будут сливать 2 потока.
Создайте пустой файл main.cpp и скопируйте в него код из файла main_lsd2.cpp.
Классы EvenSplitter и OddSplitter выполняют слияние чётных и нечётных элементов массивов соответственно.
class EvenSplitter:public task
{
private:
double *mas;
double *tmp;
int size1;
int size2;
public:
EvenSplitter(double *_mas, double *_tmp, int _size1,
int _size2): mas(_mas), tmp(_tmp),
size1(_size1), size2(_size2)
{}
task* execute()
{
for(int i=0; i<size1; i+=2)
tmp[i] = mas[i];
double *mas2 = mas + size1;
int a = 0;
int b = 0;
int i = 0;
while( (a < size1) && (b < size2))
{
if(tmp[a] <= mas2[b])
{
mas[i] = tmp[a];
a+=2;
}
else
{
mas[i] = mas2[b];
b+=2;
}
i+=2;
}
if (a == size1)
for(int j=b; j<size2; j+=2,i+=2)
mas[i] = mas2[j];
else
for(int j=a; j<size1; j+=2,i+=2)
mas[i] = tmp[j];
return NULL;
}
};
class OddSplitter:public task
{
private:
double *mas;
double *tmp;
int size1;
int size2;
public:
OddSplitter(double *_mas, double *_tmp, int _size1,
int _size2): mas(_mas), tmp(_tmp),
size1(_size1), size2(_size2)
{}
task* execute()
{
for(int i=1; i<size1; i+=2)
tmp[i] = mas[i];
double *mas2 = mas + size1;
int a = 1;
int b = 1;
int i = 1;
while( (a < size1) && (b < size2))
{
if(tmp[a] <= mas2[b])
{
mas[i] = tmp[a];
a+=2;
}
else
{
mas[i] = mas2[b];
b+=2;
}
i+=2;
}
if (a == size1)
for(int j=b; j<size2; j+=2,i+=2)
mas[i] = mas2[j];
else
for(int j=a; j<size1; j+=2,i+=2)
mas[i] = tmp[j];
return NULL;
}
};
Класс SimpleComparator выполняется сравнение чётных и нечётных пар элементов массива, проходя по массиву один раз.
class SimpleComparator
{
private:
double *mas;
int size;
public:
SimpleComparator(double *_mas, int _size): mas(_mas), size(_size)
{}
void operator()(const blocked_range<int>& r) const
{
int begin = r.begin(), end = r.end();
for(int i=begin; i<end; i++)
if(mas[2*i] < mas[2*i-1])
{
double _tmp = mas[2*i-1];
mas[2*i-1] = mas[2*i];
mas[2*i] = _tmp;
}
}
};Класс LSDParallelSorter как и ранее реализует рекурсивный алгоритм слияния, выполняя последовательную сортировку, в том случае, если размер сортируемой порции массива меньшее, чем значение поля portion (значение этого поля задаётся при создании объекта в функции LSDParallelSortDouble()).
class LSDParallelSorter:public task
{
private:
double *mas;
double *tmp;
int size;
int portion;
public:
LSDParallelSorter(double *_mas, double *_tmp, int _size,
int _portion): mas(_mas), tmp(_tmp),
size(_size), portion(_portion)
{}
task* execute()
{
if(size <= portion)
{
LSDSortDouble(mas, tmp, size);
}
else
{
int s = size/2 + (size/2)%2;
LSDParallelSorter &sorter1 = *new (allocate_child())
LSDParallelSorter(mas, tmp, s, portion);
LSDParallelSorter &sorter2 = *new (allocate_child())
LSDParallelSorter(mas + s, tmp + s, size - s,
portion);
set_ref_count(3);
spawn(sorter1);
spawn_and_wait_for_all(sorter2);
EvenSplitter &splitter1 = *new (allocate_child())
EvenSplitter(mas, tmp, s, size - s);
OddSplitter &splitter2 = *new (allocate_child())
OddSplitter(mas, tmp, s, size - s);
set_ref_count(3);
spawn(splitter1);
spawn_and_wait_for_all(splitter2);
parallel_for(blocked_range<int>(1, (size+1)/2),
SimpleComparator(mas, size));
}
return NULL;
}
};
Соберите получившуюся реализацию для Intel Xeon Phi и проведите тест для 10 миллионов элементов при разном числе потоков на сопроцессоре. Результаты, полученные авторами на Intel Xeon Phi, представлены на рис. 4.6.
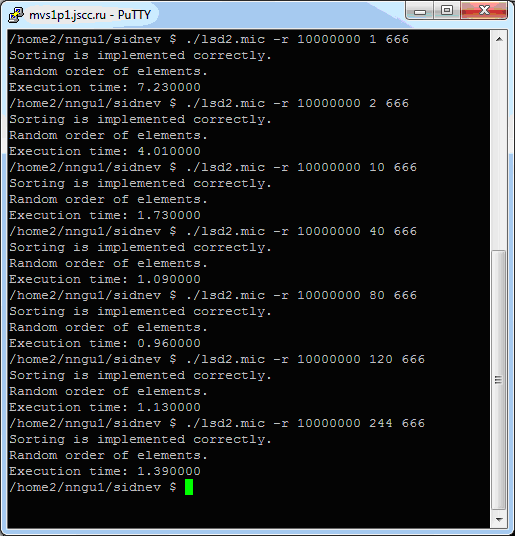
Рис. 4.6. Результаты параллельной побайтовой восходящей сортировки при использовании чётно-нечётного слияния Бэтчера на Intel Xeon Phi
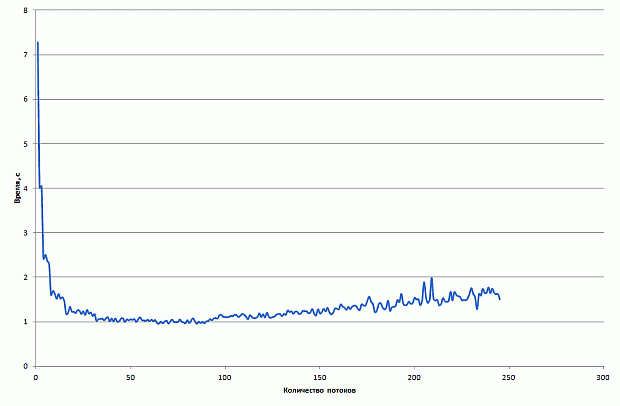
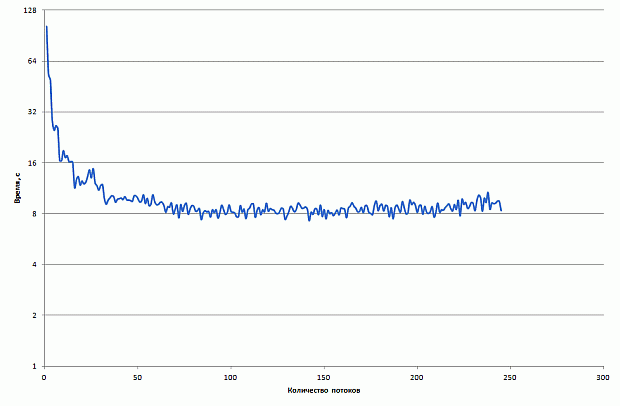
Здесь мы запускали только вариант со случайным заполнением, но с разным числом потоков. Результаты очень похожи на предыдущие. Для наглядности приведём графики времени сортировки 10 миллионов ( рис. 4.7) и 100 миллионов ( рис. 4.8) элементов с помощью параллельного алгоритма LSD с использованием чётно-нечётного слияния Бэтчера на сопроцессоре.
увеличить изображение
Рис. 4.7. Время сортировки 10 миллионов элементов с помощью параллельного алгоритма LSD с использованием чётно-нечётного слияния Бэтчера на Intel Xeon Phi
увеличить изображение
Рис. 4.8. Время сортировки 100 миллионов элементов с помощью параллельного алгоритма LSD с использованием чётно-нечётного слияния Бэтчера на Intel Xeon Phi
Максимальное ускорение, равное 14.1, достигается при использовании 142 потоков.