|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Самостоятельная работа 5: Оптимизация вычислений в задаче матричного умножения. Оптимизация работы с памятью
Последовательная реализация алгоритма умножения матриц
Попробуем разработать собственную реализацию алгоритма умножения матриц. В начале, реализуем алгоритм согласно определению. Затем попробуем повысить эффективность реализации с точки зрения времени вычислений.
Базовая реализация алгоритма умножения матриц
Реализуем алгоритм умножения согласно определению.
//single.cpp
#include "mult.h"
void mult(ELEMENT_TYPE * A, ELEMENT_TYPE * B,
ELEMENT_TYPE * C, int n)
{
ELEMENT_TYPE s;
int i, j, k;
for(j = 0; j < n; j++ )
for(i = 0; i < n; i++ )
C[j * n + i] = 0;
for(i = 0 i < n; i++ )
for(j = 0; j < n; j++ )
for(k = 0; k < n; k++ )
C[j * n + i] += A[j * n + k] * B[k * n + i];
}
Укажем в строке компиляции файл с реализацией алгоритма:
icpc -mmic –mkl=parallel -openmp ./single.cpp ./main.cpp ./routine.cpp –osingle
Скомпилируем и запустим приложение.
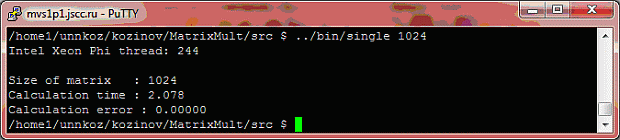
На рис. 10.2 представлен результат работы программы.
Итак, мы видим (таблица 10.4), что при N = 1024 время работы составляет около 57с. При этом время работы аналогичной (более сложной) функции в библиотеке MKL составляет около 0,1с. Для определенности сделаем запуск для N = 1025. Заметим, что время работы нашей программы существенно сократилось, в то время как время работы функции из MKL осталось прежним. Мистика или объективная реальность?
| N | Наивная реализация | MKL sequential | MKL parallel |
| 1024 | 57,34 | 0,207 | 0,004 |
| 1025 | 33,09 | 0,200 | 0,004 |
Попробуем ответить на поставленный вопрос. Тот факт, что время работы первой наивной реализации сильно отличается от "эталона", не является сюрпризом. Разработчики высокопроизводительных библиотек хорошо знают свое дело. А вот существенное сокращение времени при увеличении размера на единицу – более чем странный факт. Причина может быть найдена при помощи профилировщика, который обнаружит, что при размере матрицы N = 1024 мы обращаемся в память с таким шагом, что нужные нам данные должны быть загружены в одну и ту же кеш-линию. В результате кеш-память используется крайне неэффективно: при следующей операции с данными мы вынуждены вытеснить кеш-линейку, которую недавно загружали и планировали использовать далее, тогда как значительная часть других кеш-линеек не используется. При размере матрицы N = 1025 этого не происходит. Слушателям предлагается составить фрагмент карты обращений в память с учетом того, что кеш является 8-ассоциативным, размер кеш-линии составляет 64 байта, размер кеш-памяти составляет 32KB. Данная карта поможет понять рассмотренный выше эффект, а также пригодится для дальнейшего изучения вопроса эффективного использования кеш-памяти.
Влияние порядка циклов на скорость вычислений
Посмотрев внимательно на карту обращений в память, составленную ранее, можно заметить, что мы обращаемся в память не в том порядке, в котором храним данные ( рис. 10.3). Попробуем изменить порядок циклов и исследуем вопрос о том, как это влияет на время работы программы.
Всего существует шесть возможных перестановок. Попробуем каждую из них для экспериментального определения оптимального порядка циклов. Разработку реализаций алгоритма при разных порядках циклов предлагается провести самостоятельно.
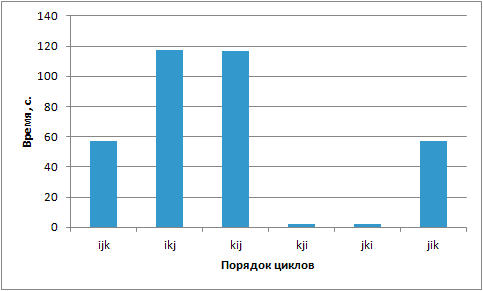
В таблице 10.5 представлены времена вычислений:
| Ijk | Ikj | Kij | Kij | jki | jik | MKL seq. |
| 57,34 | 117,5 | 116,81 | 2,149 | 12,084 | 56,904 | 0,207 |
Почему времена так сильно отличаются?
Одна из главных причин низкой производительности при "неправильном порядке" циклов – плохо организованная работа с памятью. Современные процессоры чувствительны к тому, в каком порядке происходит чтение и запись в память. Чувствительность связана со сложной архитектурой организации памяти, как процессоров, так и сопроцессоров [6]. Если чтение и запись происходит последовательно, то процессор может это предсказать и заранее загрузить данные в кэш-память. Доступ к кэш-памяти гораздо быстрее доступа к оперативной памяти. Кроме того, данные в кэш-память загружаются не поэлементно, а сразу группами (размер кэш-линейки равный 64 КБ.). Если из кеш-линии использовать только один элемент, то много данных будет загружено в процессор и не использовано в вычислениях. Обратим внимание на то, что обращение к элементам матриц A и B таково, что многие элементы читаются и используются в кеш-памяти (при больших размерах матриц) один раз.
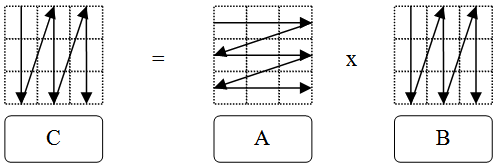
В реализации алгоритма умножения матриц из раздела 4.1 (порядок циклов ijk соответствующий определению), обход матрицы происходит, как показано на рис. 10.4.
Учитывая, что матрицы хранятся непрерывным вектором, обход матриц B и С не оптимален (хоть и имеет регулярный характер). Значительную роль в снижение производительности играет обход матрицы B. Элементы матрицы B используются 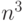 раз, а матрицы С –
раз, а матрицы С –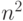 раз.
раз.
При оптимальном порядке циклов jki обход матриц показан на рис. 10.5. Доступ к элементам стал последовательным. Как следствие, повысилась производительность.
На рис. 10.6 представлен результат вычислений при лучшем расположении циклов.
Следует отметить, что низкая производительность программ из-за неудачно организованной работы с памятью является общей тенденцией и проявляется не только при реализации алгоритма умножении матриц, но во многих других практически значимых задачах.