Программирование на языке MC#
В этом разделе, использование специфических конструкций языка MC# будет проиллюстрировано на ряде параллельных и распределенных программ. Также излагаются и иллюстрируются общие принципы построения MC#-программ для нескольких типичных задач параллельного программирования. Подчеркиваются различия при разработке параллельных программ, предназначенных для исполнения на системах с общей памятью (например, мультиядерных процессорах), и распределенных программ, исполняющихся на сети машин (вычислительном кластере).
5.1. Вычисление чисел Фибоначчи
Последовательность чисел Фибоначчи есть бесконечный ряд из натуральных чисел
a0, a1, a2, a3, . . .
таких, что
a0 = 1, a1 = 1, и ai = ai-1 + ai-2, для i >= 2.
Построим параллельную программу, находящую n -ое ( n >= 0 ) число в ряду Фибоначчи, т.е., элемент an последовательности.
Первый вариант такой программы будет иметь рекурсивную структуру, соответствующую формуле определения чисел Фибоначчи. Основной вычислительный метод этой программы будет объявлен асинхронным, и будет возвращать вычисленный результат по каналу, переданному ему в качестве одного из входных аргументов. С другой стороны, в рекурсивных вызовах внутри этого метода будут использоваться каналы для получения значений от методов, вызванных рекурсивно.
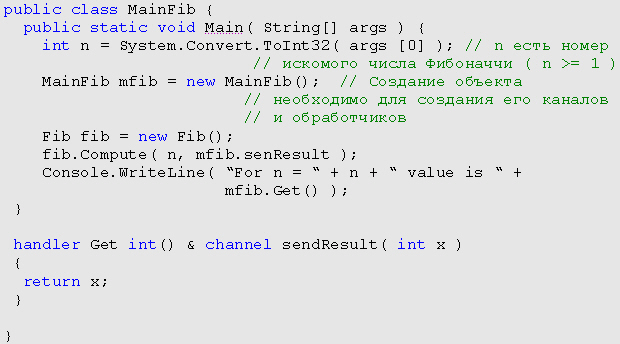
Класс Fib, содержащий основной вычислительный метод Compute, может иметь следующий вид:
Главный класс для этой программы может выглядеть следующим образом:
Упражнение 1. Показать, почему при рекурсивных вызовах функции Compute необходимо создание новых объектов класcа Fib.
( Подсказка: рассмотреть как будут использоваться каналы ic1 и ic2 в программе, в которой опущено создание таких объектов, например, при вызове функции Compute с n = 3).
Легко видеть, что приведенный вариант параллельной программы является очень неэффективным, поскольку в нем порождается 2n асинхронных вызовов метода Compute, каждый из которых выполняет очень мало вычислительных операций: фактически, порождает два дополнительных вызова и передает результат по каналу. Очевидно, что в этом случае эффект от параллельного исполнения методов будет перекрыт накладными расходами на их порождение.
Избежать порождения асинхронных вызовов функции Compute для малых по величине аргументов n можно путем введения "локального" вычисления соответствующей функции для малых n:
Приведенный выше вариант является более эффективным, чем первый, но и он обладает существенным недостатком: теперь async-методы для больших n выполняют очень мало вычислительных операций.
Сократить общее количество порождаемых рекурсивно async-методов и более равномерно распределить по ним вычислительную нагрузку позволяет следующий, "линейный" вариант программы Fib:
Приведенные выше рассуждения и варианты программы Fib переносятся и на варианты этой же программы, но для распределенного исполнения (т.е., с заменой async на movable ). При этом, для получения максимального ускорения программист должен подобрать оптимальное значение константы threshold.
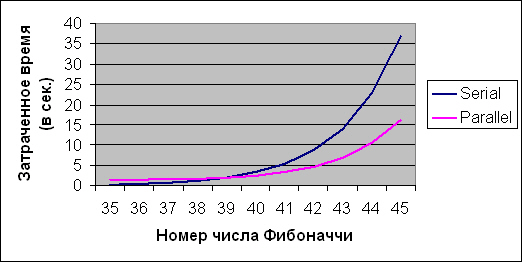
Ниже приведены графики времени выполнения последовательной программы и распределенного, "линейного" варианта программы Fib с threshold = 36. Причем количество используемых процессоров в распределенном варианте определялось как n - 34 (для n >= 35 ). Тестовые замеры проводились на кластере с процессорами AMD Athlon(TM) MP 1800+.
Полные тексты вариантов программы Fib приведёны в приложении [ "Программирование на языке MC#" ].
5.2. Обход бинарного дерева
Если структура данных задачи организована в виде дерева, то его обработку легко распараллелить путем обработки каждого поддерева отдельном async- ( movable- ) методом.
Предположим, что мы имеем следующее определение (в действительности, сбалансированного) бинарного дерева в виде класса BinTree:
Тогда просуммировать значения, находящиеся в узлах такого дерева (и, в общем случае, произвести более сложную обработку) можно с помощью следующей программы, структура которой, по существу, совпадает со структурой предыдущей программы Fib:
Естественно, что для повышения эффективности этой программы, а именно, для получения ускорения при исполнении ее на параллельной архитектуре, необходимо внести в нее усовершенствования, аналогичные тем, которые были сделаны для программы Fib.
Следует также отметить, что в случае распределенного варианта этой программы, при вызове movable -метода Sum, к объекту класса BinTree, являющемуся аргументом этого метода, будут применяться процедуры сериализации/десериализации при переносе вычислений на другой компьютер. (В действительности, с точки зрения Runtime-языка MC#, поддерживающей распределенное исполнение программ, канал также является обычным объектом, к которому будут применяться процедуры сериализации/десериализации).
Полный текст данной программы приведён в приложении [ "Программирование на языке MC#" ].
Упражнение 2. Предположим, что имеется класс Tree, внутренними полями которого являются поле value, хранящее значение, связанное с корнем данного дерева, и поле subtrees, являющееся массивом объектов класса Tree.
Написать параллельную программу на MC#, суммирующую значения из всех вершин заданного дерева.
( Подсказка: для получения значений от рекурсивно порождаемых методов, воспользуйтесь одним каналом).