|
не хватает одного параметра: static void Main(string[] args) |
Программные проекты на C#
Сортировка. Описание Решения Sorting
Решение Sorting содержит проекты, позволяющие провести сравнительный анализ эффективности последовательных и параллельных алгоритмов сортировки массивов. В проектах анализируются три алгоритма:
- пузырьковой сортировки;
- быстрой сортировки;
- сортировки Бэтчера.
Первые две сортировки рассматриваются в учебном курсе. Сортировка Бэтчера, которая создавалась как сортировка, предназначенная для параллельного выполнения, в текст учебника не вошла. Одна из причин в том, что хотя алгоритм сортировки достаточно прост, но объяснение его корректности совсем не просто.
Структура Решения Sorting
Решение Sorting содержит 3 проекта. Следуя принципу разделения интерфейса и бизнес-логики, содержательная часть реализована в проекте ClassLibrary Sorting, представляющем динамическую библиотеку классов. Библиотека содержит один класс – Sorting, включающий методы, реализующие последовательные и параллельные алгоритмы сортировки массива.
Для пузырьковой сортировки построен метод, реализующий последовательную классическую версию, и метод, реализующий параллельный вариант пузырьковой сортировки. Параллельный вариант реализует идею шагового алгоритма. Сортируемый массив разбивается на k групп, в каждую из которых включаются элементы, отстоящие на расстоянии k. Все группы сортируются параллельно, а затем выполняется последовательная операция слияния k-упорядоченных групп в единый массив.
Для быстрой сортировки наряду с последовательной версией рассматриваются два параллельных метода – один реализует идею шагового алгоритма, другой – реализует рекурсивный вариант сортировки с ограниченным распараллеливанием.
Для рекурсивного варианта с ограничением на параллелизм в зависимости от объема массива вызывается либо последовательная версия либо параллельная версия, использующая инструментарий параллельных задач (класс Task). Этот вариант в лекциях курса не рассматривался, хотя, как можно будет увидеть по результатам экспериментов, он наиболее эффективен при сортировке больших массивов.
Для сортировки Бэтчера построены две параллельные версии. Одна реализует алгоритм, описанный в третьем томе "Искусство программирования" - фундаментальном труде Дональда Кнута. Эта версия (у Кнута это явно не оговорено) корректно работает только тогда , когда размер массива N является степенью двойки. Вторая версия работает для массивов любого размера.
Два проекта WindowsFormsSorting и ConsoleSorting являются интерфейсным проектами. Первый удобен при проведении запланированных исследований, второй – при проведении экспериментов, проверки различных возникающих гипотез.
Сортировка. Результаты и Выводы
Рассмотрим результаты экспериментов по анализу сравнительной эффективности последовательных и параллельных алгоритмов. Посмотрим, что может дать параллельный вариант пузырьковой сортировки в сравнении с его последовательным собратом:
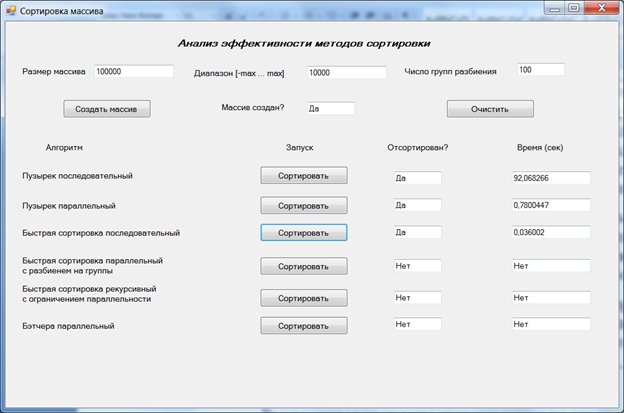
Рис. 9.7. Сравнительный анализ эффективности последовательного и параллельного алгоритмов пузырьковой сортировки
Результаты показывают, что параллельный вариант "пузырька" сортировки массива из 100 000 элементов при разбиении массива на 100 групп эффективнее по времени более чем в 100 раз, затрачивая на сортировку менее секунды, в то время, когда последовательный вариант затрачивает более полутора минут. Как видите, распараллеливание дает существенный эффект. Радость этого успеха слегка портит тот факт, что существует другой последовательный алгоритм, который сортирует этот массив еще быстрее. Можно видеть, что последовательный алгоритм быстрой сортировки справляется с задачей на порядок лучше параллельного пузырька, затрачивая на сортировку сотые доли секунды.
Главный вопрос, на какой хотелось получить ответ при изучении методов сортировки, можно ли предложить параллельный вариант сортировки, работающий быстрее последовательного варианта быстрой сортировки? В тексте лекций положительного ответа так и не было дано. Приведу результаты, показывающие, что параллельные методы сортировки могут работать быстрее последовательного метода:
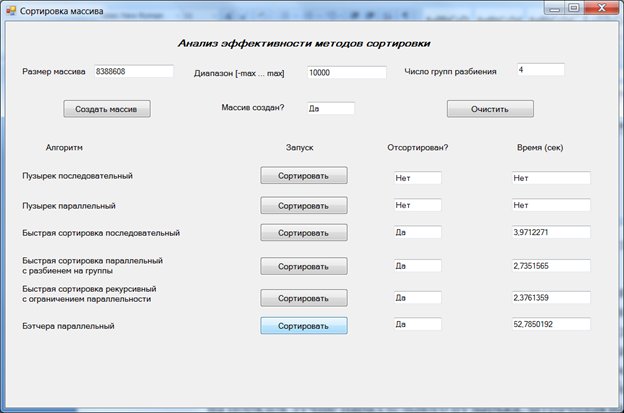
Рис. 9.8. Сравнительный анализ эффективности последовательного алгоритма и параллельных алгоритмов быстрой сортировки (2-х ядерный компьютер)
Как можно видеть, на массиве из 8 388 608 элементов обе параллельные версии быстрой сортировки работают существенно быстрее последовательного варианта быстрой сортировки. Лучший результат показывает рекурсивная версия с ограниченной параллельностью, в которой для массивов размера менее 100 000 элементов вызывается рекурсивная последовательная версия, а для массивов большего размера создаются две параллельно работающие задачи.
Размер массива в данном эксперименте может показаться на первый взгляд странным, но он выбран таковым для того, чтобы можно было использовать лучшую по эффективности версию сортировки Бэтчера, накладывающую ограничения на размер массива (в данном случае N = 223).
О сортировке Бэтчера следует сказать особо. В этом эксперименте она показала наихудший результат, затратив на порядок больше времени, чем последовательная версия. Эта сортировка построена на операциях "сравнение – обмен", рассматриваемых как единое целое. Вначале сравниваются пары элементов массива, после чего массив становится дву- упорядоченным. На следующем этапе новые пары сравниваются таким образом, что поволяют получить четырех-упорядоченный массив. Затем строятся восьмерки упорядоченности, пока массив не будет полностью упорядочен. Все операции "сравнение – обмен" можно выполнять параллельно. Теоретически ожидается, что сортировка Бэтчера, несмотря на сложность организации, при распараллеливании вычислений работает быстрее в сравнении с последовательными вариантами . Но практика не всегда совпадает с теорией.
Ситуация здесь примерно такая же, как и с пирамидальным алгоритмом суммирования. Теоретически, обладая сложностью порядка O(logN), пирамидальный алгоритм должен работать значительнее эффективнее по времени, чем последовательный алгоритм со сложностью O(N). Но на практике это не так, поскольку на малых N последовательный алгоритм обогнать практически невозможно и нецелесообразно, а для больших значений N накладные расходы на организацию параллелизма не только съедают весь выигрыш от распараллеливания вычислений, но и приводят к дополнительным существенным затратам. Вот и в алгоритме Бэтчера накладные расходы слишком велики, чтобы им стоило пользоваться для сортировки больших массивов в рассматриваемых усовиях.
Следует заметить, что данные по сортировке массива приведены по результатам экспериментов на 2-х ядерном 32-х разрядном компьютере. Вот как выглядят в тех же условиях результаты работы на 4-х ядерном 64-х битном компьютере:
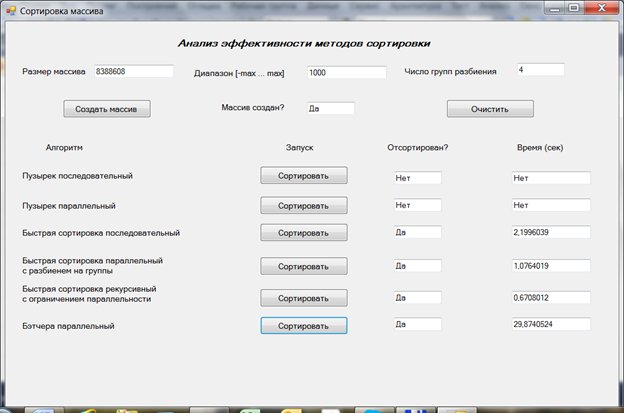
Рис. 9.9. Сравнительный анализ эффективности последовательного алгоритма и параллельных алгоритмов быстрой сортировки (4-х ядерный компьютер)
Как видите, с увеличением числа ядер параллельные алгоритмы улучшают свои показатели в сравнении с последовательным алгоритмом. Первый из параллельных алгоритмов показывает результаты вдвое лучше последовательного алгоритма, второй – более чем в три раза.
Подводя общие итоги сравнительного анализа методов сортировки, следует сказать, что для массивов сравнительно небольшого размера (до миллиона элементов) сортировка относится в нашей классификации к задачам второго класса, где существует эффективный последовательный алгоритм, делающий нерациональным применение параллельных вычислений. Однако современная тенденция состоит в том, что оперативная память может быть очень большой, позволяющая, например, вести в оперативной памяти работу с большими базами данных. В этом случае приходится сортировать массивы с сотнями миллионов элементов. В таких ситуациях параллельные версии сортировки эффективны. Как показывают наши исследования, эффективные параллельные версии сортировки существуют, так что задачу сортировки сверхбольших массивов следует отнести к задачам третьего класса.
