|
не хватает одного параметра: static void Main(string[] args) |
Параллельные вычисления
Четыре проблемы параллельных вычислений
В заключение первой главы кратко рассмотрим некоторые проблемы, возникающие при организации параллельных вычислений.
Синхронизация
Когда несколько модулей одной и той же программы запускаются на разных процессорах, то возникает необходимость в синхронизации их действий.
Модулю А могут быть необходимы результаты работы модулей В и С, поэтому начать свое выполнение модуль А может лишь по завершении работы как модуля В, так и модуля С, которые могут выполняться параллельно, но не известно, какой из них первым закончит работу. В любом случае запуск модуля А на выполнение должен быть синхронизирован с окончанием работ модулей В и С.
При распараллеливании по данным один и тот же модуль F может быть запущен на k процессорах и параллельно выполняться, обрабатывая разные подмножества данных 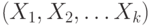 . Результаты работы k процессоров затем объединяются в процессе работы модуля G. Понятно, что запуск на выполнение модуля G должен быть синхронизирован с окончанием работы модуля F на всех параллельно работающих k процессорах.
. Результаты работы k процессоров затем объединяются в процессе работы модуля G. Понятно, что запуск на выполнение модуля G должен быть синхронизирован с окончанием работы модуля F на всех параллельно работающих k процессорах.
Параллельные вычисления требуют тщательной синхронизации работы модулей программы, выполняемых разными процессорами.
Гонка данных (Data race)
Так называемая проблема "гонки данных" возникает для мультипроцессорных компьютеров с общей памятью. Поскольку процессоры работают параллельно, то в одни и те же моменты времени они могут получать доступ к одним и тем же данным, хранимым в общей памяти, как для чтения, так и для записи.
Если совместное чтение данных представляется возможным и допустимым, то одновременная запись двух разных значений в одну и ту же ячейку памяти не допустима. Запись всегда будет идти по очереди. Конкурирование процессоров за запись в одно и то же слово памяти и называется "гонкой данных". Интересно, что в этой гонке выигрывает не тот, кто пришел первый, а тот, кто пришел последний, поскольку именно его результаты будут сохранены в памяти. Это соответствует пословице: "хорошо смеется тот, кто смеется последним".
Чтобы справиться с проблемой "гонки данных", существуют разные механизмы закрытия памяти - одного из видов совместно используемого ресурса. Тот, кто выигрывает гонку и приходит первым, закрывает ресурс для доступа. Проигравшие гонку прерывают выполнение и становятся в очередь за обладание ресурсом. Обладатель ресурса спокойно выполняет свою работу, а по ее окончании открывает ресурс, с которым теперь начинает работать тот, кто первым стоит в очереди.
Гонка данных - это одна из самых серьезных проблем параллельного программирования, поскольку при некорректно организованной блокировке ресурса программа может завершаться с некорректными результатами без возникновения исключительных ситуаций.
Плохо, когда в процессе работы программы происходит отказ и нужные нам результаты не могут быть получены. Но еще хуже, когда программа завершается, выдает результаты, но эти результаты ошибочны. Плохо, когда студент на экзамене говорит: "не знаю", но хуже, когда он говорит "глупости".
Клинч или смертельные объятия (deadlock)
Чтобы справиться с гонкой данных, приходится включать блокировку, закрывая ресурс для других конкурентов, которые должны прервать свою работу и томиться в очереди, ожидая момента освобождения ресурса. Блокировка - полезный механизм, обойтись без которого в ряде ситуаций просто невозможно. Но блокировка - это и опасный механизм, порождающий прерывание работы всей программы, когда возникает ситуация, называемая тупиком, клинчем или смертельным объятием.
Рассмотрим простейшую ситуацию, приводящую к возникновению клинча. Пусть есть два конкурента А и В, претендующие на два ресурса f и g. Пусть гонку за ресурс f выиграл А и соответственно закрыл этот ресурс для В. Гонку за ресурс g выиграл В и закрыл ресурс для А. Но А, чтобы закончить свою работу нужен ресурс g, поэтому он стал в очередь, ожидая освобождения ресурса g. Симметрично, В томится в очереди, ожидая освобождения ресурса f. Возникает ситуация клинча, когда ни А, ни В не могут продолжить свою работу.
В боксе, когда два боксера входят в клинч, сцепившись друг с другом, нужен судья, дающий команду "break", чтобы боксеры могли разойтись и продолжить бой. Так и в параллельных вычислениях при возникновении клинча, только внешнее воздействие может разрешить ситуацию.
Послать - Получить (Send - Receive или Map - Reduce)
Для мультикомпьютерных комплексов, где каждый компьютер комплекса имеет собственную память, проблемы гонки данных и клинча не столь актуальны. Здесь возникает своя не менее серьезная проблема. Хотя каждый компьютер комплекса работает со своими данными, но все параллельно работающие компьютеры решают одну и ту же задачу, поэтому без обмена информацией обойтись невозможно. В процессе работы компьютеры должны обмениваться данными, посылая друг другу сообщения. В кластерах (типичном виде мультикомпьютерного комплекса) компьютеры объединены высокоскоростными линиями связи. Тем не менее, передача данных является медленной операцией, и время на передачу данных может "съесть" весь выигрыш, полученный за счет распараллеливания вычислений. Поэтому при анализе эффективности работы программы, работающей на кластере или другом мультикомпьютерном комплексе, где параллельно работающие процессоры обмениваются сообщениями по линиям связи, не имея доступа к общей памяти, важную роль играют операции п осылки и получения сообщений (send - receive, map - reduce).
Пусть на кластере, содержащем k компьютеров, нужно решить некоторую задачу D на множестве данных X.
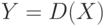
Алгоритм решения может быть задан следующей схемой:
Map(X); //Исходное множество X разбивается на k подмножеств, каждое из которых
//пересылается на соответствующий компьютер кластера.
Parallel_D(Xi); //Задача D параллельно запускается на каждом компьютере,
//обрабатывая подмножество данных Xi, и получая результат Yi.
Reduce(Y); //Результаты работы каждого компьютера Yi объединяются, создавая общее
//решение Y.Для последовательного алгоритма время решения исходной задачи может быть записано в виде:
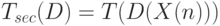 |
( 1.37) |
Для параллельного алгоритма время решения исходной задачи может быть записано в виде:
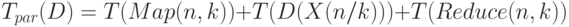 |
( 1.38) |
Как правило, Map и Reduce имеют линейную сложность. Полагая, что архитектура кластера позволяет одновременно пересылать данные всем компьютерам кластера, можно записать следующие соотношения для времени выполнения этих операций:
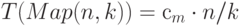
Аналогично
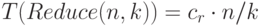
Какой же алгоритм предпочтительнее по времени выполнения - последовательный или параллельный? В этих условиях все зависит от сложности задачи D. Если это простая задача с линейной временной сложностью
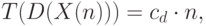
то вероятнее всего последовательный алгоритм будет эффективнее, поскольку обычно константы 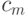 и
и 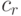 много больше константы
много больше константы 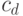 . Так что будет выполняться соотношение:
. Так что будет выполняться соотношение:
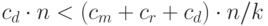
Для этого достаточно выполнения условия:
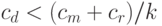
Для сложной в вычислительном отношении задачи D параллельный алгоритм, скорее всего, окажется эффективнее. Так, для задачи D, имеющей кубическую сложность, выполнение условия:
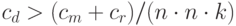
гарантирует эффективность параллельного алгоритма.
На этом завершим первую главу. В последующих главах появятся конкретные примеры, иллюстрирующие положения, рассмотренные в этой главе.
