Типовые информационные структуры
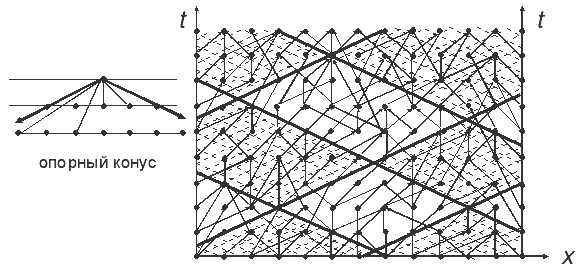
Локальный алгоритм. Яркий пример нерегулярного локального алгоритма дает использование явной схемы на нерегулярной или адаптивной сетке. На рис. 9.9 приведен некоторый гипотетический пример. Граф локальный, имеет полный набор разверток. С помощью разверток осуществляется разбиение алгоритма на параллельно выполняемые фрагменты. На рис. 9.9 графы фрагментов заштрихованы.
Очень "простой" пример. Этот пример не был взят ни из
теории, ни из практики. Он специально придуман для того, чтобы
показать, насколько сложными могут быть информационные связи даже у
вроде бы самых простых алгоритмов. Формально данный пример реализует
некоторую сортировку из  чисел. Впоследствии выяснилось, что он
является очень хорошим тестом для проверки того, насколько эффективно
та или иная технология определяет параллелизм в записях алгоритмов.
Заметим, что на этом тесте "сломались",
т.е. не смогли обнаружить никакого параллелизма, все доступные нам
параллелизующие компиляторы и автономные системы как отечественные,
так и зарубежные. Пример записывается следующим образом:
чисел. Впоследствии выяснилось, что он
является очень хорошим тестом для проверки того, насколько эффективно
та или иная технология определяет параллелизм в записях алгоритмов.
Заметим, что на этом тесте "сломались",
т.е. не смогли обнаружить никакого параллелизма, все доступные нам
параллелизующие компиляторы и автономные системы как отечественные,
так и зарубежные. Пример записывается следующим образом:
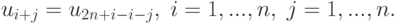
 i, ни по
i, ни по  . Однако если
алгоритм записать несколько иначе, именно
. Однако если
алгоритм записать несколько иначе, именно
 операции по
операции по  в каждой из двух групп уже
можно выполнять параллельно. Сами же группы надо по-прежнему выполнять
последовательно. Граф рассматриваемого алгоритма действительно устроен
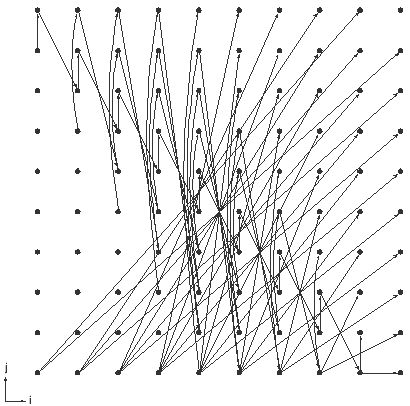
очень сложно. Это видно хотя бы по рис. 9.10, на котором граф
изображен для
в каждой из двух групп уже
можно выполнять параллельно. Сами же группы надо по-прежнему выполнять
последовательно. Граф рассматриваемого алгоритма действительно устроен
очень сложно. Это видно хотя бы по рис. 9.10, на котором граф
изображен для 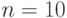 .
.В связи с рассмотренными примерами обратим внимание на следующее обстоятельство. Несмотря на внешнее разнообразие, графы многих алгоритмов имеют немало общего. Точнее, с помощью не очень сложных преобразований их можно свести не только к регулярным графам, но и к регулярным графам с координатными векторами связей за счет некоторого усложнения вершин-операций. Мы уже видели, что даже произвольный локальный граф поддается такому преобразованию. Техника проведения подобных преобразований частично была описана ранее. Более детально применительно к разным ситуациям с ней можно познакомиться в [ 1 ] .
Построение графов для большого числа конкретных алгоритмов выявило удивительную закономерность: большое разнообразие алгоритмов не приводит к такому же разнообразию информационных структур. Многие графы формально различных алгоритмов оказались изоморфными в главном, отличаясь друг от друга содержанием вершин и дуг. Например, на всем множестве алгоритмов линейной алгебры различных по существу типов графов оказалось всего лишь порядка десятка. Все это привело к предположению, что, возможно, верна
Гипотеза. Типовых информационных структур алгоритмов в конкретных прикладных областях немного.
Пока практика подтверждает эту гипотезу. Если гипотеза о типовых структурах окажется верной, то откроется много новых связей и направлений исследований. Изложение численных методов может быть поставлено на общий информационный фундамент, распараллеливание типовых информационных структур может быть заранее изучено и реализовано с помощью специальных программных средств, по типовым структурам могут быть построены спецпроцессоры, осуществляющие быстрое решение нужных алгоритмов. Отсюда уже недалеко и до построения заказных вычислительных систем, ориентированных на эффективное решение классов задач из конкретных прикладных областей. В частности, математические модели спецпроцессоров для таких заказных систем вполне можно строить, используя описанную ранее гомоморфную свертку графов тех же самых типовых структур.