Системные данные числового типа

3.8. Операции над числовыми данными целого типа

Над целочисленными данными (константами и переменными) в языках C, C++ можно выполнять обычные арифметические операции - сложение ( x+y ), вычитание ( z-5 ), умножение ( x1*x3 ) и деление ( y/w ). В отличие от языка Pascal здесь деление целочисленных операндов дает целочисленный результат. Например, 5/2=2. Для получения остатка от деления в C, C++ используется операция %, например, 5%2=1.

Целочисленные данные можно подвергать операции сдвига как влево (знак операции - <<), так и вправо (знак операции - >>) на заданное количество двоичных разрядов:

y=x<<3; // сдвиг влево на три двоичные разряда
z=y>>5; // сдвиг вправо на пять двоичных разрядов

Операция сдвига вправо работает по-разному для целых чисел со знаком и целых чисел без знака. Внимательно посмотрите на результат работы следующей программы:

#include <stdio.h>
#include <conio.h>
int main()
{
  int x=5, y=-5;
  unsigned z=0xFFFFFFFB;
  printf("x=%x y=%x z=%x",x,y,z);
  printf("\nx<<2=%x x>>2=%x",x<<2,x>>2);
  printf("\ny<<2=%x y>>2=%x",y<<2,y>>2);
  printf("\nz<<2=%x z>>2=%x",z<<2,z>>2);
  getch();
  return 0;
}
//=== Результат работы ===
x=5 y=fffffffb z=fffffffb
x<<2=20 x>>2=1
y<<2=ffffffec y>>2=fffffffe
z<<2=ffffffec z>>2=3ffffffe

Дело в том, что для чисел со знаком операция сдвига на n разрядов эквивалентна умножению на 2ⁿ при сдвиге влево или делению на 2ⁿ при сдвиге вправо. Поэтому для отрицательного операнда результат сдвига должен остаться отрицательным. С этой целью при сдвиге вправо производится размножение знакового разряда.

Над одноименными двоичными разрядами целочисленных операндов могут выполняться логические операции - логическое сложение (символ операции ' | '), логическое умножение (символ операции ' & '), исключающее ИЛИ (символ операции ' ^ ') и инвертирование (символ операции ' ~ '). Приведенная ниже программа иллюстрирует выполнение указанных операций над переменными x=5 (двоичный код 00...0101 ) и y=7 (двоичный код 00...0111 ).

#include <stdio.h>
#include <conio.h>
int main()
{
  int x=5, y=7;
  printf("x=%x y=%x",x,y);
  printf("\nx|y=%x x&y=%x",x|y,x&y);
  printf("\nx^y=%x ~x=%x",x^y,~x);
  getch();
  return 0;
}
//=== Результат работы ===
x=5 y=7
x|y=7 x&y=5
x^y=2 ~x=fffffffa

Определенную помощь при обработке целочисленных данных могут оказать системные функции математической библиотеки. Прототипы этих функций описаны в заголовочных файлах math.h и stdlib.h. Мы упомянем лишь некоторые из них.

Функция abs(x) возвращает модуль своего аргумента. Аргументом функций atoi(s) и atol(s) является строка, представляющая запись целого числа. Каждая из этих функций преобразует символьную запись числа в соответствующий машинный формат (результат atoi имеет тип int, результат atol - тип long ) и возвращает полученный результат. Довольно полезное преобразование выполняют функции itoa и ltoa. Первый их аргумент - числовое значение типа int или long. Вторым аргументом является строковый массив (или указатель на строку), куда записывается результат преобразования. А третий аргумент, значение которого находится в диапазоне от 2 до 36, определяет основание системы счисления, в которую преобразуется значение первого аргумента.

В ряде математических алгоритмов, использующих вероятностные методы (методы Монте-Карло), а чаще - в игровых программах активно используются различные датчики случайных чисел. Функция random(N) при каждом повторном обращении к ней выдает очередное случайное число из диапазона от 0 до N-1. Эти числа имеют равномерное распределение вероятностей, что можно трактовать следующим образом. Допустим, мы обратились к функции random(1000) 1000 раз. Можно утверждать, что среди полученных чисел почти все будут разными. Конечно, на практике это не совсем так, но вероятность того, что среди полученных чисел встретится много одинаковых, близка к нулю. Для игровых программ очень важно, чтобы при обращении к датчику случайных чисел каждый раз возникала непредсказуемая последовательность. С этой целью можно обратиться к функции randomize(), которая случайным образом возмущает начальное состояние программы, генерирующей случайные числа.

Продемонстрируем использование датчика случайных чисел на примере программы перемешивания колоды карт. Предположим, что для идентификации карт использованы целые числа в диапазоне от 0 до 35 (или до 51). Идея алгоритма перемешивания состоит в многократной генерации случайных чисел от 0 до 35 и перекладывания первой карты с k-той ( k - очередное случайное число). Организуем пятикратное перемешивание, чтобы убедиться в том, что каждый раз колода оказывается в новом непредсказуемом состоянии.

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>

void mixer(char *b)
{ int j;
  char i,tmp;
  randomize();
  for(j=0; j<10000; j++)
  { i=random(36);
    tmp=b[0]; b[0]=b[i]; b[i]=tmp;
  }
}

int main()
{ char j,k,a[36];
  printf("\nPlaying-cards before:\n");
  for(k=0; k<36; k++)
  { a[k]=k; printf("%4d",a[k]); }
  for(j=0; j<5; j++)
  { mixer(a);
    printf("\nPlaying-cards after %d:\n",j);
    for(k=0; k<36; k++)
      printf("%4d",a[k]);
  }
  getch();
  return 0;
}
//=== Результат работы ===
Playing-cards before:
   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35
Playing-cards after 0:
   9   0  13  32  18  30  14  24  34  28   7  26  35  16   3  27   5  11   6
  23  21   8  31  17  29   2  15  22  33  12  19  25   1   4  10  20
Playing-cards after 1:
  28   9  16   1   6  19   3  29  10  33  24  15  20   5  32  22  30  26  14
  17   8  34  25  11  12  13  27  31   4  35  23   2   0  18   7  21
Playing-cards after 2:
  33  28   5   0  14  23  32  12   7   4  29  27  21  30   1  31  19  15   3
  11  34  10   2  26  35  16  22  25  18  20  17  13   9   6  24   8
Playing-cards after 3:
   4  33  30   9   3  17   1  35  24  18  12  22   8  19   0  25  23  27  32
  26  10   7  13  15  20   5  31   2   6  21  11  16  28  14  29  34
Playing-cards after 4:
  18   4  19  28  32  11   0  20  29   6  35  31  34  23   9   2  17  22   1
  15   7  24  16  27  21  30  25  13  14   8  26   5  33   3  12  10

3.9. Операции над числовыми данными вещественного типа

При вычислениях с вещественными данными разрешается использовать только четыре арифметические операции - сложение (+), вычитание (-), умножение (*) и деление (/). В арифметическом выражении могут встречаться операнды разных типов, поэтому важно знать, как компилятор определяет тип результирующего значения. Правило это довольно простое, но оно содержит подводные камни. Арифметические действия выполняются в соответствии общепринятыми правилами:

• сначала выполняются действия в самых внутренних скобках;
• внутри скобок порядок действий определяется приоритетом операций - сначала одноместные операции типа смены знака, инвертирования и вычисления функций, затем умножения и деления и, в самую последнюю очередь, сложения и вычитания;
• тип результата функции описан либо в системных заголовочных файлах, либо в программе пользователя;
• тип операнда, представленного сомножителями, определяется типом самого "продвинутого" сомножителя (т.е. допускающего самый широкий диапазон представления данных);
• тип выражения, состоящего из слагаемых, определяется типом самого "продвинутого" слагаемого.

Несмотря на простоту и естественность описанных выше правил, результаты вычисления некоторых выражений могут поставить в тупик не очень внимательного программиста. Например, не вызывает сомнения, что тип выражения 5/2+1.0 должен быть вещественным. Однако к вещественным данным относятся и значения типа float, и значения типа double, и значения типа long double. В данном случае, компилятор ориентируется на тип числовой константы 1.0, которая по правилам системы программирования преобразуется в машинный формат длинного вещественного числа (т.е. имеет тип double ). А вот результат вычисления данного выражения равен 3.000000, и это может вызвать недоумение. На самом деле, тип каждого слагаемого формулы определяется независимо от типов других слагаемых. Первое слагаемое представлено частным от деления двух целых констант, поэтому его тип тоже целый, т.е. результат деления равен 2, а не 2.5. Затем значения всех слагаемых приводятся к типу double, и итоговый результат равен 3.0.

Существенную помощь в вычислениях с вещественными данными оказывают многочисленные математические функции из раздела math.h. Список некоторых из них приведен в табл. 3.7.

Прототипы функций max и min, которые, на самом деле представлены не настоящими функциями, а соответствующими макроопределениями, содержатся в файле stdlib.h.

Для большинства функций типа double с аргументом типа double имеются их аналоги с данными типа long double. Названия этих функций отличаются от приведенных в табл. 3.7 добавкой окончания l - (fabs, fabsl), (acos, acosl), ...:

Особо следует остановиться на функциях округления ceil и floor. Первая из них возвращает наименьшее целое значение, которое больше или равно x. Вторая возвращает наибольшее целое значение, не превосходящее x. Обратите внимание на то, что значение, возвращаемое обеими функциями, представлено в формате double.

ceil(0.1) =1.0			floor(0.1) = 0.0
ceil(0.5) =1.0			floor(0.5) = 0.0
ceil(0.9) =1.0			floor(0.9) = 0.0
ceil(-0.9)=0.0			floor(-0.9)=-1.0
ceil(-0.5)=0.0			floor(-0.5)=-1.0
ceil(-0.1)=0.0			floor(-0.1)=-1.0

Довольно часто программисты используют для округления функцию floor(x+0.5). Однако иногда она выдает результат, не совпадающий с общепринятым в математике, например floor(-0.5+0.5)=0. Конечно, жаль, что в языках C, C++ нет прямого аналога функции round из Паскаля, но построить такую функцию совсем не сложно:

int round(double x)
{ int res;
  res=(x<0)? x-0.5 : x+0.5;
  return res;
}

Если нужно произвести округление в том или ином знаке, то число можно предварительно разделить или умножить на 10^k, округлить, а затем результат округления умножить или разделить на 10^k.

Замечание 1. При выводе числовых результатов вещественного типа необходимые округления производят системные программы вывода.

Замечание 2. Если целочисленной переменной присваивается вещественное значение, то округление не производится. Дробная часть, какой бы она ни была, просто отбрасывается.

В заголовочном файле math.h приводятся определения именованных констант, которыми полезно воспользоваться в своих программах (см. табл. 3.8).

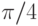
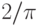
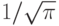
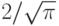
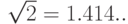Таблица 3.8.

Константа	Значение	Константа	Значение
M_PI		M_E	e=2.718...
M_PI_2		M_LOG2E	log2e
M_PI_4		M_LOG10E	log e
M_2_PI		M_LN2	ln 2
M_1_SQRTPI		M_LN10	ln 10
M_2_SQRTPI		M_SQRT2	.
		M_SQRT_2