Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы
Проблема самоприменимости заключается в проверке для каждой программы  с входной переменной x и выходной переменной y того, остановится ли
с входной переменной x и выходной переменной y того, остановится ли  на собственном номере
на собственном номере  , т.е в вычислении
всюду определенной функции
, т.е в вычислении
всюду определенной функции

Теорема 10.4. Проблема самоприменимости алгоритмически неразрешима, т.е. не существует структурированной программы, вычисляющей функцию Fs(x).
Доказательство от противного. Предположим, что существует программа P, вычисляющая функцию Fs(x). Без ограничения общности, можно считать,
что ее выходная переменная есть y (почему?) и поэтому 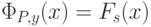 для всех x. Пусть переменная z не входит в P.
Рассмотрим следующую программу P’:
для всех x. Пусть переменная z не входит в P.
Рассмотрим следующую программу P’:
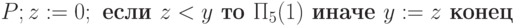
Легко проверить, что если P на входе x выдает результат y=1, то P’
на этом входе не останавливается, а если P выдает результат y=0, то P’
останавливается ( и тоже выдает 0). Пусть n’=nP’ - номер программы P’.
Чему тогда равно значение 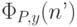 ?
Если оно равно 1, то на входе x=n’ программа P’ не остановится, т.е.
?
Если оно равно 1, то на входе x=n’ программа P’ не остановится, т.е. 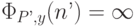 , но тогда
, но тогда  .
Если же
.
Если же 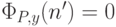 , то P’ на входе x=n’ останавливается с результатом 0,
т.е.
, то P’ на входе x=n’ останавливается с результатом 0,
т.е. 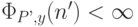 . Но тогда
. Но тогда 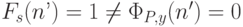 .
Во всех случаях получили, что
.
Во всех случаях получили, что 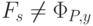 и, следовательно,
предположение о существовании программы для вычисления функции Fs
неверно.
и, следовательно,
предположение о существовании программы для вычисления функции Fs
неверно.
Заметим, что на самом деле мы доказали отсутствие структурированной программы для вычисления функции Fs. Но тезис Тьюринга-Черча и эквивалентность структурированных программ машинам Тьюринга и ч.р.ф. позволяют сделать вывод об алгоритмической неразрешимости рассматриваемой проблемы.
Проблема самоприменимости может показаться не очень интересной с практической ("программистской") точки зрения. Но оказывается, что ее можно использовать для доказательства алгоритмической неразрешимости многих других алгоритмических проблем, более тесно связанных с практикой программирования.
-
Проблема останова: по произвольной структурированной программе
 определить завершится ли вычисление
определить завершится ли вычисление  на входе 0, т.е вычислить всюду определенную функцию
на входе 0, т.е вычислить всюду определенную функцию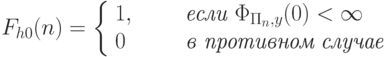
В более общем виде проблема останова состоит в вычислении следующей функции:
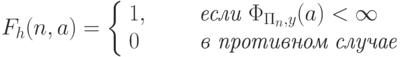
Из этого определения следует, что программа
 останавливается
на входе a тогда и только тогда, когда Fh(n,a)=1.
останавливается
на входе a тогда и только тогда, когда Fh(n,a)=1. -
Проблема тотальности: по произвольной структурированной программе
 определить, завершает ли она работу при всех значениях входной переменной, т.е вычислить всюду определенную функцию
определить, завершает ли она работу при всех значениях входной переменной, т.е вычислить всюду определенную функцию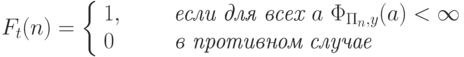
-
Проблема эквивалентности: по произвольным двум структурированным программам
 и
и  определить, эквивалентны ли они, т.е вычисляют ли они одну и ту же функцию:
определить, эквивалентны ли они, т.е вычисляют ли они одну и ту же функцию: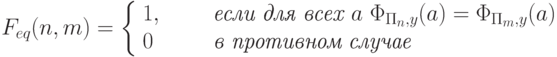
-
Проблемы оптимизации текста программы. Одна из возможных оптимизаций (текста) программы состоит в удалении из нее операторов присваивания, которые никогда не работают, а другая - в замене условных операторов вида

на
 в случае, когда условие
в случае, когда условие  истинно на любых входных данных, и - на
истинно на любых входных данных, и - на 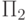 , если оно на любом входе
ложно. Определим соответствующие этим оптимизациям функции:
, если оно на любом входе
ложно. Определим соответствующие этим оптимизациям функции:
Из этого определения следует, что при Fopt1(n,m)=0 программу
 можно оптимизировать, удалив из нее m -ый оператор присваивания. Назовем задачу вычисления функции Fopt1(n,m) проблемой лишнего присваивания
можно оптимизировать, удалив из нее m -ый оператор присваивания. Назовем задачу вычисления функции Fopt1(n,m) проблемой лишнего присваивания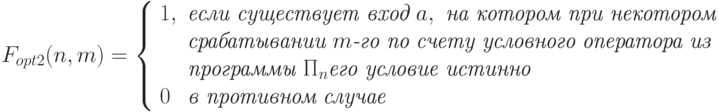
Ясно, что при Fopt2(n,m)=0 программу
 можно оптимизировать, заменив ее m -ый условный оператор его второй альтернативой.
Назовем задачу вычисления функции Fopt2 (n,m) проблемой лишнего условия
можно оптимизировать, заменив ее m -ый условный оператор его второй альтернативой.
Назовем задачу вычисления функции Fopt2 (n,m) проблемой лишнего условияЗаметим, что проблема самоприменимости и все проблемы, перечисленные в пп. 1-4 выше, связаны с вычислением функций, принимающих два значения 0 и 1. Эти функции являются характеристическими функциями соответствующих множеств. Например, Fh0(n) является характеристической функцией множества номеров программ, останавливающихся на входе 0. Напомним, что для множества
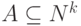 его характеристическая функция cAk определяется следующим образом:
его характеристическая функция cAk определяется следующим образом: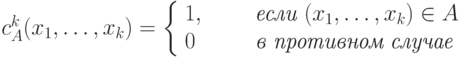
На множества переносится понятия разрешимости и неразрешимости.
Определение 10.1. Множество 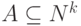 назовем разрешимым (или рекурсивным ), если его характеристическая функция cAk вычислима, т.е. является общерекурсивной функцией,
в противном случае, оно (и связанная с ним проблема) неразрешимо.
назовем разрешимым (или рекурсивным ), если его характеристическая функция cAk вычислима, т.е. является общерекурсивной функцией,
в противном случае, оно (и связанная с ним проблема) неразрешимо.
Используя это определение, теорему 10.4 можно переформулировать так:
Множество номеров программ, остановливающихся на собственном номере,
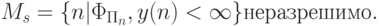
Обычно доказательства неразрешимости проблем используют метод сведения. Неформально его идею можно сформулировать следующим образом: "Если решение некоторой неразрешимой проблемы A можно эффективно получить, используя решение проблемы B, то тогда проблема B тоже неразрешима."
Определим отношение сводимости более формально.
Напомним, что нумерационные функции позволяют вместо
наборов (векторов, n -ок) целых чисел рассматривать их номера.
Для множества 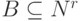 обозначим через cr(B) множество номеров входящих в B наборов:
обозначим через cr(B) множество номеров входящих в B наборов: 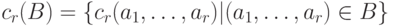 (при r=1, разумеется, c1(B)=B ).
(при r=1, разумеется, c1(B)=B ).
Лемма 10.1.
Множество (проблема) 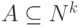 сводится
к множеству (проблеме)
сводится
к множеству (проблеме) 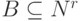 , если существует общерекурсивная функция f: Nk -> N
такая, что
, если существует общерекурсивная функция f: Nk -> N
такая, что 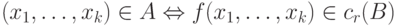 .
В этом случае будем писать A <=m B посредством f.
.
В этом случае будем писать A <=m B посредством f.
Содержательно, " A сводится к B посредством f " означает, что для выяснения, входит ли x в A, можно эффективно преобразовать x в такие входные данные y=f(x)
проблемы B, что при 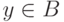 имеем
имеем 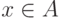 , а если
, а если 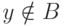 , то и
, то и 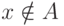 .
.
Разрешимые множества сводятся к любым нетривиальным множествам.
Лемма 10.2. Если A разрешимо, а B не совпадает с  и N, то A <=m B.
и N, то A <=m B.
Доказательство. По условию имеются такие b и d, что 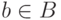 , а
, а 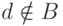 .
Положим f(x) = b , cA(x) + d ,(1 - cA(x)). Тогда при
.
Положим f(x) = b , cA(x) + d ,(1 - cA(x)). Тогда при 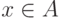 имеем
имеем 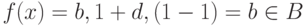 ,
а при
,
а при 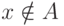 -
- 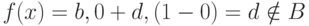 . Таким образом, A <=m B посредством f.
. Таким образом, A <=m B посредством f.
Как мы уже отмечали, доказательство неразрешимости можно основывать на следующем утверждении.
Лемма 10.3. Если A сводится к B и проблема A неразрешима, то и проблема B неразрешима.
Доказательство. Пусть A <=m B посредством f. Тогда из определения сводимости следует, что для всех x имеет место равенство cA(x)=cB(f(x)). Поэтому, если бы B была разрешима, то ее характеристическая функция cB была бы общерекурсивна и cA также была бы общерекурсивна. Но это противоречит неразрешимости проблемы A.
