Алгоритмы: частично рекурсивные функции
Программная вычислимость рекурсивных функций
В этом параграфе рассмотрим соотношение между программно вычислимыми и частично рекурсивными функциями. Справедлива следующая
Теорема 8.1. Каждая частично рекурсивная функция программно вычислима.
Доказательство индукцией по определению ч.р.ф.
Базис: программная вычислимость простейших функций была установлена в примерах 1.1, 1.2 и 1.4.
Индукционный шаг: покажем программную вычислимость операторов суперпозиции, примитивной рекурсии и минимизации.
Суперпозиция. Пусть Fm и f1n,..., fmn
- арифметические функции, вычислимые программами 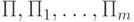 так, что
так, что 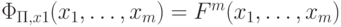 , и
, и  при i=1,...,n. Пусть переменные y1, ..., ym, z1,..., zn
не используются в программах
при i=1,...,n. Пусть переменные y1, ..., ym, z1,..., zn
не используются в программах 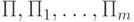 . Кроме того, пусть все вспомогательные переменные этих программ - это w1, ... , wr. Рассмотрим следующую программу P:
. Кроме того, пусть все вспомогательные переменные этих программ - это w1, ... , wr. Рассмотрим следующую программу P:
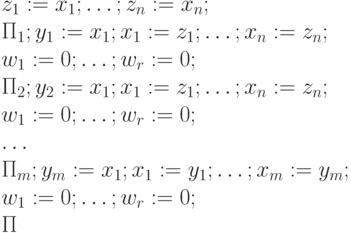
В качестве входных переменных зафиксируем x1, ..., xn, а выходной - x1. Пусть в исходном состоянии x1=a1, ..., xn = an. Тогда в первой строке эти значения сохраняются в переменных z1, ..., zn, которые своих значений далее не меняют. Поэтому для каждого i=1,...,m-1 после выполнения фрагмента

значением переменной yi является fin(a1,..., an), x1=a1, ..., xn = an, а значения всех вспомогательных переменных равны 0. Тогда после выполнения

значением каждого xi также является fin(a1,..., an),
а после выполнения  значение x1 равно
значение x1 равно 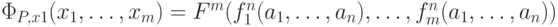 .
Таким образом,
.
Таким образом, ![\Phi _{P, x1} = [F; f_{1}, \dots , f_{n}]](/sites/default/files/tex_cache/a3276a916028c02a30dd206da4b918d6.png) .
.
Примитивная рекурсия.
Рассмотрим для простоты случай n=1. Пусть функция F2(x1,y) получена с помощью оператора примитивной рекурсии из функций g1(x1) и h3(x1, y, z), т.е. F2 =R(g1,h3).
Предположим, что существуют программы  и
и 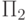 , вычисляющие функции g1 и h3 так, что
, вычисляющие функции g1 и h3 так, что 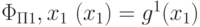 и
и  .
Пусть вспомогательные переменные
.
Пусть вспомогательные переменные 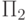 - это z1,..., zm и они не встречаются в
- это z1,..., zm и они не встречаются в  , а переменные u1, y1 и v не используются в программах
, а переменные u1, y1 и v не используются в программах  и
и 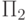 .
Рассмотрим программу P:
.
Рассмотрим программу P:  пока v < y1 делай z:=x1; x1:=u1; y:=v;
пока v < y1 делай z:=x1; x1:=u1; y:=v;  все
В качестве входных переменных P возьмем x1 и y,
а выходной - x1.
все
В качестве входных переменных P возьмем x1 и y,
а выходной - x1.
Рассмотрим работу P на исходном состоянии 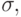 в котором
в котором 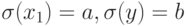 . При b=0 цикл не выполняется и в результирующем состоянии
. При b=0 цикл не выполняется и в результирующем состоянии 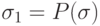 имеем
имеем 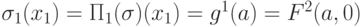 . При b > 0 цикл будет выполняться b раз, так как в его теле v всякий
раз увеличивается на 1, а значение y1=b и не меняется. Перед первым
выполнением
. При b > 0 цикл будет выполняться b раз, так как в его теле v всякий
раз увеличивается на 1, а значение y1=b и не меняется. Перед первым
выполнением 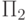 все ее рабочие переменные zi равны 0, x1=a, y=0, z=F2(a, 0), а после ее выполнения x1=h3(a,0,F(a,0))=F(a,1).
Предположим теперь по индукции, что перед (i+1) -ым выполнением
все ее рабочие переменные zi равны 0, x1=a, y=0, z=F2(a, 0), а после ее выполнения x1=h3(a,0,F(a,0))=F(a,1).
Предположим теперь по индукции, что перед (i+1) -ым выполнением 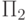 все ее рабочие переменные zi равны 0, x1=a, y=i и z=F2(a, i).
После этого выполнения x1=h3(a,i,z)=h3(a,i,F(a,i))=F(a,i+1). Тогда присваивания z1:=0; ... ; zm:=0; v:= v+1 после
все ее рабочие переменные zi равны 0, x1=a, y=i и z=F2(a, i).
После этого выполнения x1=h3(a,i,z)=h3(a,i,F(a,i))=F(a,i+1). Тогда присваивания z1:=0; ... ; zm:=0; v:= v+1 после 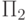 и z:=x1; x1:=u1; y:=v; перед ее следующим выполнением установят значения переменных
и z:=x1; x1:=u1; y:=v; перед ее следующим выполнением установят значения переменных 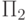 так, что все ее рабочие переменные zi равны 0, x1=a, y=i+1 и z=F2(a, i+1). Следовательно, после b -го выполнения тела цикла x1=h3(a,b-1,F(a,b-1))=F(a,b).
так, что все ее рабочие переменные zi равны 0, x1=a, y=i+1 и z=F2(a, i+1). Следовательно, после b -го выполнения тела цикла x1=h3(a,b-1,F(a,b-1))=F(a,b).
Минимизация. Предположим, что функция Fn(x1,... ,xn) получена с помощью оператора минимизации ( mu -оператора) из функции gn+1(x1,..., xn,y), т.е.
![F^n(x_1,\ldots, x_n) =\mu y[ g^{n+1}(x_1,\ldots, x_n,y)=0].](/sites/default/files/tex_cache/1787bb402a96c840f3444cb7fe8f80fb.png)
Пусть программа  вычисляет gn+1, так что
вычисляет gn+1, так что 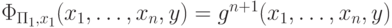 ,
и пусть рабочие переменные
,
и пусть рабочие переменные  - это z1,..., zm. Зафиксируем переменные x1',... , xn', y';, u, z, не входяшие в
- это z1,..., zm. Зафиксируем переменные x1',... , xn', y';, u, z, не входяшие в 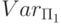 .
Рассмотрим следующую программу
.
Рассмотрим следующую программу 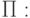
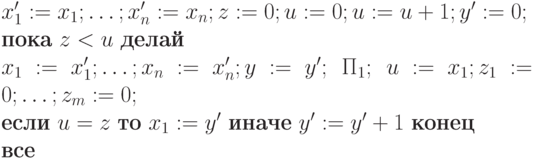
Рассмотрим работу  на входных значених xi = ai (i=1,...,n).
В первой строке они сохраняются в переменных x'i, которые
нигде в
на входных значених xi = ai (i=1,...,n).
В первой строке они сохраняются в переменных x'i, которые
нигде в  не изменяются, z получает значение 0, которое тоже не меняется по ходу вычисления,
а u вначале получает значение 1. Поэтому условие цикла после первой строки
истинно и
он хотя бы один раз выполняется.
Докажем, что для каждого i >= 1, (i+1) -ая итерация цикла выполняется
тогда и только тогда, когда g(a1, ..., an,0)=b1 >0, ..., g(a1, ..., an, i-1)=bi-1 > 0,
не изменяются, z получает значение 0, которое тоже не меняется по ходу вычисления,
а u вначале получает значение 1. Поэтому условие цикла после первой строки
истинно и
он хотя бы один раз выполняется.
Докажем, что для каждого i >= 1, (i+1) -ая итерация цикла выполняется
тогда и только тогда, когда g(a1, ..., an,0)=b1 >0, ..., g(a1, ..., an, i-1)=bi-1 > 0,  останавливается после (i+1) -ой итерации цикла с результатом x1=i
тогда и только тогда, когда g(a1, ..., an,i)=0.
При этом
перед выполнением
останавливается после (i+1) -ой итерации цикла с результатом x1=i
тогда и только тогда, когда g(a1, ..., an,i)=0.
При этом
перед выполнением  входные переменные x1,...,xn,y имеют значения a1,...,an, i, соответственно, y'= i, а все рабочие переменные zj (j=1,..., m) равны 0.
входные переменные x1,...,xn,y имеют значения a1,...,an, i, соответственно, y'= i, а все рабочие переменные zj (j=1,..., m) равны 0.
Действительно, предположив это условие, получим, что после очередного выполнения фрагмента
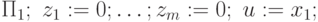
значение u = x1 = g(a1,...,an,i), а рабочие переменные восстанавливают нулевые значения.
Если g(a1,...,an,i)=0, то u=z и в условном операторе x1 получает
значение y'=i. После этого условие цикла нарушено и  завершает работу с выходным
значением x1=i =F(a1,..., an).
Если же g(a1,...,an,i)> 0, то u>z и в условном операторе y' увеличивает значение до (i+1).
Тогда условие цикла выполнено и перед (i+2) -ым выполнением
завершает работу с выходным
значением x1=i =F(a1,..., an).
Если же g(a1,...,an,i)> 0, то u>z и в условном операторе y' увеличивает значение до (i+1).
Тогда условие цикла выполнено и перед (i+2) -ым выполнением  ее входные переменные x1,...,xn,y имеют значения a1,...,an, i+1, соответственно, y'= i+1, а все рабочие переменные равны 0.
ее входные переменные x1,...,xn,y имеют значения a1,...,an, i+1, соответственно, y'= i+1, а все рабочие переменные равны 0.
Из доказанного утверждения непосредственно следует, что
![\Phi_{\Pi,x_1}(a_1,\ldots,a_n)= \mu y[g(a_1,\ldots,a_n,y)=0].](/sites/default/files/tex_cache/1ff75ed0a2034589c8f76349c1afe445.png)
Имеет место и утверждение, обратное теореме 8.1, которое мы приводим здесь без доказательства.
Теорема 8.2. Каждая программно вычислимая функция является частично рекурсивной.
