Элементы векторной алгебры. Векторы. Координаты векторов. Линейные операции над векторами

Операции над векторами

Сложение и вычитание

Сложение и вычитание векторов производят математически (по формулам) или геометрически (рис. 5.5). Геометрический способ более известен как правило треугольника.

Рис. 5.5.

Математически сложение записывают 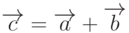или 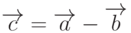, если речь идет о вычитании векторов (рис. 5.5). В координатной форме эти операции над векторами можно определить следующим образом. Пусть в пространстве заданы два разных вектора a =(a_x;a_y;a_z) и b =(b_x;b_y;b_z). Требуется определить вектор с, равный c=a+b или c=a-b. Чтобы математически выполнить сложение или вычитание, сложим или вычтем соответствующие компоненты исходных векторов: c=a+b =(a_x+b_x;a_y+b_y;a_z+b_z) или c=a-b =(a_x-b_x;a_y-b_y;a_z-b_z).

Если в пространстве задано несколько векторов, число которых больше двух, то операцию сложения (вычитания) записывают как .

Геометрически этот способ называют правилом многоугольника.

Непосредственно из геометрического определения суммы (разности) векторов следует два свойства операции сложения (разности), в справедливости которых можно легко убедиться самостоятельно:

• коммутативность суммы, т.е. ;
• ассоциативность суммы, т.е. .
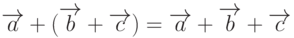