Эксперименты по контролю функции выходов инициального автомата
Контроль функции выходов инициального автомата с использованием простого безусловного эксперимента
Известно, что ДУ с памятью, описываемое математической моделью конечного автомата Мили, всегда может быть реализовано в виде, изображенном на рис.6.1. Здесь блок  реализует функцию выходов и является комбинационным устройством, а блок
реализует функцию выходов и является комбинационным устройством, а блок  представляет собой запоминающее устройство.
представляет собой запоминающее устройство.
В общем случае причинами неисправности ДУ могут быть как неисправности в блоке  (блоке
(блоке  ), так и неисправности, возникшие в обоих блоках.
), так и неисправности, возникшие в обоих блоках.
В этой лекции рассматриваются эксперименты, ориентированные на контроль функционирования блока  , т. е. функции выхода автомата. Мы займемся исследованием этого частного случая экспериментов потому, что для проверки памяти ДУ, т. е. блока
, т. е. функции выхода автомата. Мы займемся исследованием этого частного случая экспериментов потому, что для проверки памяти ДУ, т. е. блока  , разработаны хорошо зарекомендовавшие себя специальные методы. Конечно, для проверки функционирования блока
, разработаны хорошо зарекомендовавшие себя специальные методы. Конечно, для проверки функционирования блока  можно применить контрольные эксперименты общего вида, однако в рассмотренной ситуации методы их построения не учитывают ее специфики и будут порождать тесты, длина которых заведомо больше той, которая минимально необходима.
можно применить контрольные эксперименты общего вида, однако в рассмотренной ситуации методы их построения не учитывают ее специфики и будут порождать тесты, длина которых заведомо больше той, которая минимально необходима.
Естественно, что методы контроля зависят от класса рассматриваемых автоматов и применяемых средств. Ниже исследуются методы контроля для инициальных и неинициальных автоматов, а в качестве средств используются простые и кратные безусловные эксперименты. Характерной особенностью всех рассматриваемых здесь задач контроля является их сводимость к построению различных обходов графов автомата, т. е. путей по графу, проходящих через все его дуги.
Поскольку в рамках теории графов рассматриваются более общие конструкции, чем автоматные графы, полезно попытаться найти решение задачи построения обхода графа, не обязательно являющегося автоматным. Из решения этой более общей задачи решение соответствующей автоматной задачи будет следовать как частный случай.
В связи с этим при исследовании рассматриваемых ниже задач будем придерживаться следующей схемы: после постановки задачи контроля она будет сводиться к задаче построения соответствующего обхода графа. Далее в терминах теории графов будут получены условия существования решения, алгоритмы построения решения и оценки длины получаемых обходов.
При решении задач контроля автоматов обычно принимается предположение, что в процессе проведения эксперимента дополнительных неисправностей в автомате не возникает. В рассматриваемых ниже задачах это предположение также остается в силе.
Рассмотрим следующую задачу. Пусть в распоряжении экспериментатора находится один экземпляр автомата Мили  , у которого известны входной алфавит
, у которого известны входной алфавит 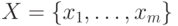 , выходной алфавит
, выходной алфавит 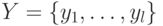 , множество состояний
, множество состояний  , где
, где  - выделенное состояние, называемое начальным, и функция переходов
- выделенное состояние, называемое начальным, и функция переходов  . Требуется построить простой безусловный эксперимент, позволяющий распознать функцию выходов
. Требуется построить простой безусловный эксперимент, позволяющий распознать функцию выходов  автомата
автомата  или эквивалентного ему автомата.
или эквивалентного ему автомата.
Умение решать сформулированную задачу позволит решать и задачу контроля функции выходов инициального автомата. В самом деле, если нам удастся распознать функцию выходов  автомата, с которым производится эксперимент, то сравнение ее с функцией
автомата, с которым производится эксперимент, то сравнение ее с функцией  автомата
автомата  , играющего роль исправного, позволит сделать вывод об исправности
, играющего роль исправного, позволит сделать вывод об исправности  в исследуемом автомате. Если же изменения, появившиеся в функционировании блока
в исследуемом автомате. Если же изменения, появившиеся в функционировании блока  , таковы, что исследуемый автомат эквивалентен
, таковы, что исследуемый автомат эквивалентен  , то естественно игнорировать эти изменения и считать исследуемый автомат исправным. Именно этим мотивируется требование распознаваемости функции выходов с точностью до эквивалентности.
, то естественно игнорировать эти изменения и считать исследуемый автомат исправным. Именно этим мотивируется требование распознаваемости функции выходов с точностью до эквивалентности.
Очевидно, что функция выходов будет распознана, если в результате проведения эксперимента для любого состояния этого автомата будет определена его реакция на любой входной символ.
В соответствии с определением простого безусловного эксперимента его проведение должно включать построение соответствующего входного слова, наблюдение реакции автомата на это входное слово и, наконец, сравнение на основе полученной реакции функции выходов исследуемого автомата с эталоном и вывод заключения об исправности ее.
Контроль функции выходов исследуемого автомата может быть выполнен с помощью так называемого контролирующего автомата, связанного с исследуемым так, как это изображено на рис.6.2, где  - исследуемый автомат,
- исследуемый автомат,  - контролирующий автомат.
- контролирующий автомат.
Автомат  фактически реализует второй и третий этап эксперимента. Вопросы синтеза подобных автоматов рассмотрены в ряде работ, например в [3], [29], поэтому мы не будем здесь на них останавливаться, а основное внимание уделим построению входного слова.
фактически реализует второй и третий этап эксперимента. Вопросы синтеза подобных автоматов рассмотрены в ряде работ, например в [3], [29], поэтому мы не будем здесь на них останавливаться, а основное внимание уделим построению входного слова.
Если автомат задан в виде ориентированного графа, у которого начальной является вершина  , то упомянутому входному слову в графе автомата будет соответствовать путь, начинающийся в
, то упомянутому входному слову в графе автомата будет соответствовать путь, начинающийся в  и проходящий через все его дуги. Этот путь будем называть обходом графа. Под путем в графе понимается последовательность дуг, таких, что конечная вершина предыдущей дуги является начальной вершиной следующей. Таким образом, сформулированная нами задача эквивалентна задаче построения обхода автоматного графа.
и проходящий через все его дуги. Этот путь будем называть обходом графа. Под путем в графе понимается последовательность дуг, таких, что конечная вершина предыдущей дуги является начальной вершиной следующей. Таким образом, сформулированная нами задача эквивалентна задаче построения обхода автоматного графа.
Под графом  , где
, где  - множество вершин и дуг графа соответственно, мы будем понимать конечный ориентированный мультиграф. Пусть
- множество вершин и дуг графа соответственно, мы будем понимать конечный ориентированный мультиграф. Пусть  - начальная вершина этого графа. Дугу
- начальная вершина этого графа. Дугу  графа, ведущую из вершины
графа, ведущую из вершины 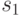 в
в 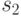 , для удобства будем иногда обозначать
, для удобства будем иногда обозначать  , чтобы явно указать ее начальную и конечную вершины.
, чтобы явно указать ее начальную и конечную вершины.
Перейдем к определению условий существования обхода графа. Рассмотрим бинарное отношение  , задаваемое следующим образом:
, задаваемое следующим образом:  тогда и только тогда, когда в графе
тогда и только тогда, когда в графе  существует путь из вершины
существует путь из вершины 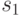 в вершину
в вершину 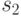 . Отношение
. Отношение  называется отношением достижимости. Используя отношение
называется отношением достижимости. Используя отношение  , построим бинарное отношение
, построим бинарное отношение  следующим образом:
следующим образом:

Известно [62], что 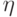 является отношением эквивалентности, а его классы, называемые слоями, являются максимальными сильно связными подмножествами множества
является отношением эквивалентности, а его классы, называемые слоями, являются максимальными сильно связными подмножествами множества  . Каждому слою
. Каждому слою  графа
графа  естественным образом ставится в соответствие подграф
естественным образом ставится в соответствие подграф  , где
, где  - множество всех дуг из
- множество всех дуг из  , начало и конец которых есть вершины множества
, начало и конец которых есть вершины множества  . Иногда для простоты мы будем отождествлять слой графа с соответствующим ему подграфом, однако каждый раз из контекста будет ясно, о чем именно идет речь.
. Иногда для простоты мы будем отождествлять слой графа с соответствующим ему подграфом, однако каждый раз из контекста будет ясно, о чем именно идет речь.
Следующее утверждение описывает класс графов, у которых существует обход.
Теорема 6.1. Для того чтобы у графа  существовал обход, необходимо и достаточно, чтобы выполнялись следующие условия:
существовал обход, необходимо и достаточно, чтобы выполнялись следующие условия:
- для любой вершины
 существует путь, связывающий вершину
существует путь, связывающий вершину  с вершиной
с вершиной  ;
; - в любом слое
 графа существует не более одной вершины
графа существует не более одной вершины  , а в графе
, а в графе  не более одной дуги
не более одной дуги  , таких, что
, таких, что  .
.
Необходимость. Предположим, что путь  является обходом графа
является обходом графа  . Справедливость первого условия непосредственно следует из определения обхода графа. Справедливость второго условия докажем от противного. Допустим, что существует слой
. Справедливость первого условия непосредственно следует из определения обхода графа. Справедливость второго условия докажем от противного. Допустим, что существует слой  и две различные дуги
и две различные дуги  и
и  , такие, что
, такие, что  и
и  . Предположим, что первая из этих дуг входит в обход ранее второй, т. е. обход имеет следующую структуру:
. Предположим, что первая из этих дуг входит в обход ранее второй, т. е. обход имеет следующую структуру:

где  - некоторые отрезки пути
- некоторые отрезки пути  .
.
Рассмотрим множество вершин  . Поскольку
. Поскольку  - сильно связное подмножество, отрезок
- сильно связное подмножество, отрезок 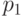 заканчивается в вершине
заканчивается в вершине  , а отрезок
, а отрезок  является начальным отрезком обхода
является начальным отрезком обхода  , то между любой вершиной
, то между любой вершиной  и вершиной
и вершиной  путь по графу
путь по графу  существует. Далее, так как отрезок
существует. Далее, так как отрезок  заканчивается в вершине
заканчивается в вершине  и
и  - сильно связное подмножество, то между вершиной
- сильно связное подмножество, то между вершиной  и любой вершиной
и любой вершиной  по графу
по графу  путь также существует. Отсюда следует, что
путь также существует. Отсюда следует, что  есть сильно связное подмножество. Это противоречит нашему предположению о том, что
есть сильно связное подмножество. Это противоречит нашему предположению о том, что  - максимальное сильно связное подмножество. Полученное противоречие и доказывает наше утверждение.
- максимальное сильно связное подмножество. Полученное противоречие и доказывает наше утверждение.
Достаточность. Поскольку рассматриваемый граф  конечен, то конечным является и число его слоев. Предположим, что это число есть
конечен, то конечным является и число его слоев. Предположим, что это число есть  .
.
Пронумеруем слои  графа
графа  следующим образом:
следующим образом:
-
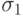 - слой, содержащий начальную вершину
- слой, содержащий начальную вершину  ;
; - пусть
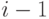 слоев
слоев  уже пронумеровано; слой
уже пронумеровано; слой  получает номер
получает номер  , если существует такая вершина
, если существует такая вершина  (
(  - слой с номером
- слой с номером 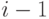 ) и такая дуга
) и такая дуга  , что
, что  ;
; - номер
 получает тот слой
получает тот слой  , все дуги которого ведут в вершины, принадлежащие
, все дуги которого ведут в вершины, принадлежащие  .
.
Легко показать, что каждому слою графа  , удовлетворяющему условию доказываемой теоремы, в соответствии со сформулированной процедурой будет присвоен единственный номер из диапазона от 1 до
, удовлетворяющему условию доказываемой теоремы, в соответствии со сформулированной процедурой будет присвоен единственный номер из диапазона от 1 до  .
.
Обозначим через  вершину слоя
вершину слоя 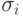 , из которой выходит дуга
, из которой выходит дуга  , такая, что
, такая, что  . В силу второго условия теоремы эта дуга единственна. Рассмотрим подграф
. В силу второго условия теоремы эта дуга единственна. Рассмотрим подграф  графа
графа  , где
, где 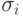 - множество вершин
- множество вершин  -го слоя,
-го слоя, 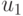 - множество всех дуг, начало и конец которых есть вершины множества
- множество всех дуг, начало и конец которых есть вершины множества 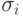 . Поскольку этот подграф сильно связен, то у него всегда существует обход
. Поскольку этот подграф сильно связен, то у него всегда существует обход 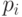 , начинающийся в вершине
, начинающийся в вершине  и заканчивающийся в вершине
и заканчивающийся в вершине  . Через
. Через 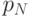 обозначим обход подграфа
обозначим обход подграфа  , начинающийся в вершине
, начинающийся в вершине  . Условимся считать, что
. Условимся считать, что  .
.
Легко видеть, что путь  является обходом графа
является обходом графа  . Достаточность условий теоремы доказана.
. Достаточность условий теоремы доказана.
Хотя приведенное доказательство теоремы 6.1 и не является конструктивным, мы не будем здесь останавливаться на методах построения обходов графа в связи с тем, что в теории графов известно много различных методов построения путей между двумя вершинами (в том числе и минимальной длины), которыми можно воспользоваться при конструировании обходов. Покажем теперь, каким образом задача построения обхода графа может быть сведена к задаче построения пути, соединяющего две его выделенные вершины.
По графу  с начальной вершиной
с начальной вершиной  построим новый граф
построим новый граф  , где
, где  - множество всех подмножеств
- множество всех подмножеств  . Начальной вершиной графа
. Начальной вершиной графа  будем считать вершину
будем считать вершину  . Положим, что в этом графе из вершины
. Положим, что в этом графе из вершины  в вершину
в вершину  ведет дуга
ведет дуга  , если:
, если:
- дуга
 графа
графа  принадлежит
принадлежит  ;
; -
 , где знаком "\" обозначена теоретико-множественная разность.
, где знаком "\" обозначена теоретико-множественная разность.
Из самой конструкции графа  легко следует справедливость следующего утверждения.
легко следует справедливость следующего утверждения.
Лемма 6.1. Путь  в графе
в графе  является его обходом тогда и только тогда, когда в графе
является его обходом тогда и только тогда, когда в графе  существует путь
существует путь

такой, что
-
 ;
; - для любого
 .
.
Лемма 6.1 по существу дает алгоритмы для решения следующих задач:
- Выяснить, существует ли обход для графа
 с начальной вершиной
с начальной вершиной  .
. - Найти множество всех обходов графа
 .
. - Найти множество всех минимальных по длине обходов графа
 .
.
Эти алгоритмы сводятся к построению по графу  графа
графа  и последующему его анализу. Так, первая задача равносильна выяснению существования пути между вершиной
и последующему его анализу. Так, первая задача равносильна выяснению существования пути между вершиной  и любой вершиной вида
и любой вершиной вида  этого графа, вторая - нахождению всех путей графа
этого графа, вторая - нахождению всех путей графа  между упомянутыми вершинами и, наконец, третья - определению всех путей минимальной длины между теми же вершинами.
между упомянутыми вершинами и, наконец, третья - определению всех путей минимальной длины между теми же вершинами.
Перейдем к интерпретации полученных результатов для задачи, сформулированной в начале этой лекции. Сделаем это достаточно подробно, чтобы далее на этом детально не останавливаться.
Легко видеть, что при построении простого безусловного эксперимента для распознавания функции выходов инициального автомата нам достаточно ограничиться рассмотрением автомата без выходов  , а не исходного автомата Мили
, а не исходного автомата Мили  , ему соответствующего.
, ему соответствующего.
Определение 6.1. Слово  будем называть характеристическим для автомата
будем называть характеристическим для автомата  , если для любого состояния
, если для любого состояния  и любого входного символа
и любого входного символа  существует начальный отрезок
существует начальный отрезок  этого слова, такой, что
этого слова, такой, что  и
и  .
.
Из этого определения следует, что характеристическое слово автомата в точности соответствует пути по графу этого автомата, начинающемуся в вершине  и проходящему через все его дуги, т. е. обходу автоматного графа. Таким образом, исходная задача сведена нами к задаче построения характеристического слова для автомата
и проходящему через все его дуги, т. е. обходу автоматного графа. Таким образом, исходная задача сведена нами к задаче построения характеристического слова для автомата  . Простая переформулировка теоремы 6.1 дает возможность описать класс автоматов, для которых характеристическое слово существует.
. Простая переформулировка теоремы 6.1 дает возможность описать класс автоматов, для которых характеристическое слово существует.
Теорема 6.1. Для того чтобы конечный инициальный автомат  обладал характеристическим словом, необходимо и достаточно, чтобы выполнялись следующие условия:
обладал характеристическим словом, необходимо и достаточно, чтобы выполнялись следующие условия:
- для любого состояния
 существует слово
существует слово  , такое, что
, такое, что  ;
; - для любого слоя
 существует не более одного состояния
существует не более одного состояния  и не более одного входного символа
и не более одного входного символа  , таких, что
, таких, что  .
.


