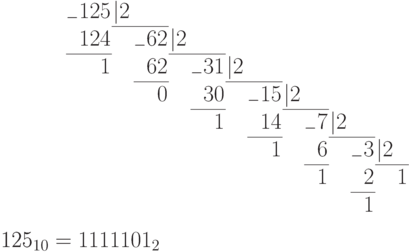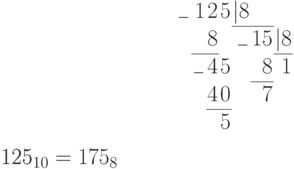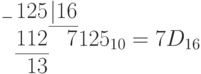НОУ ИНТУИТ | Основы цифровой техники. Лекция 11: Двоичные числа и двоичная арифметика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 21.06.2011 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 46 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассматривается двоичная система счисления как частный случай позиционной системы и основные правила двоичной арифметики.

Ключевые слова: вес, целое число, запись, аналогия, выражение, логический, основание, связь, восьмеричная система счисления, обратный код, дополнительный код, прямой, система счисления, сложение, вычитание

Принцип представления чисел в позиционных системах счисления

Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].

Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам "единицы", "десятки", "сотни", "тысячи", "десятые", "сотые", "тысячные" и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного 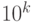$10^{k}$ , где - целое число. Например, число 125, 46 можно представить в виде суммы:

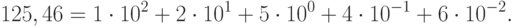
$125,46 = 1\cdot 10^{2 }+ 2\cdot 10^{1} + 5\cdot 10^{0} + 4\cdot 10^{-1} + 6 \cdot 10 ^{-2}.$

сотни десятки единицы десятые доли сотые доли

Аналогично любое число 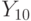$Y_{10}$ в десятичной системе счисления можно представить в виде подобной суммы:

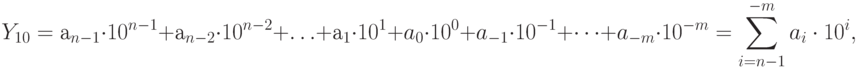$Y_{10} = а_{n-1} \cdot 10^{n-1 }+ а_{n-2} \cdot 10^{n-2 }+ … +а_{1} \cdot 10^{1} + a_{0} \cdot 10^{0} + a_{-1}\cdot 10^{-1} +…+ a_{-m}\cdot 10^{-m} = \sum\limits_{i=n-1}^{-m}{a_i \cdot 10^{i}} ,$

( 11.1)

где - количество знаков в целой части числа, - количество знаков в дробной части числа, $10^{i}$ - вес -го разряда, $а_{i}$ - весовой коэффициент для -го разряда числа. Количество возможных вариантов значения коэффициента $а_{i}$ в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков - арабские цифры "0", "1", "2", "3", "4", "5", "6", "7", "8" и "9". Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива ется аналогия между позиционными системами счисления.

Основание системы счисления - это число, равное количеству знаков, которые используются в этой системе для записи чисел.

Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:

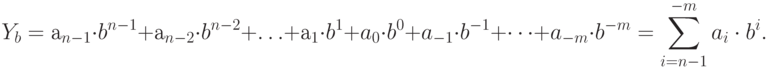$Y_{b} = а_{n-1} \cdot b^{n-1 }+ а_{n-2} \cdot b^{n-2 }+ … +а_{1} \cdot b^{1} + a_{0} \cdot b^{0} + a_{-1}\cdot b^{-1} +…+ a_{-m}\cdot b^{-m} =\sum\limits_{i=n-1}^{-m}{a_i \cdot b^{i}} .$

( 11.2)

Таблица 11.1. Параметры позиционных систем счисления
Название системы счисления	Основание системы счисления	Знаки, использующиеся для записи чисел
Двоичная	2	0, 1
Троичная	3	0, 1, 2
Четверичная	4	0, 1, 2, 3
…	…	…
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
…	…	…
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
…	…	…
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
…	…	…

С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности - это совокупность логических схем. Работа элементов этих схем основана на ключевом режиме работы транзистора, в котором он может быть только в двух состояниях, принимаемых за логический 0 и логическую 1.

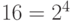Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы $8= 2^{3}$ , а основание шеснадцатиричной системы - это $16 = 2^{4}$ . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.

Итак, далее мы подробно рассмотрим именно эти позиционные системы - двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления.

Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).

Для двоичного числа:

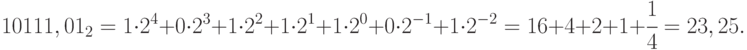
$10111,01_{2 }= 1 \cdot 2^{4} + 0\cdot 2^{3} + 1\cdot 2^{2} +1\cdot 2^{1} + 1\cdot 2^{0} + 0\cdot 2^{-1 }+1\cdot 2^{-2} = 16 + 4 + 2 + 1 + \cfrac{1}{4} = 23,25.$

Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системах записываются с указанием основания, десятичные - без этой записи.

Для восьмеричного числа:

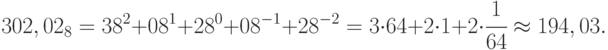
$302, 02_{8} = 3 8^{2} + 0 8^{1} + 2 8^{0} + 0 8^{-1} + 2 8^{-2} = 3 \cdot 64 + 2 \cdot 1 + 2 \cdot \cfrac{1}{64} \approx 194,03.$

Для шестнадцатеричного числа:

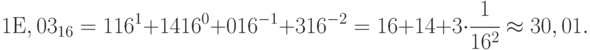
$1Е, 03_{16 }= 1 16^{1} + 14 16^{0} + 0 16^{-1} + 3 16^{-2} = 16 + 14 + 3 \cdot \cfrac{1}{16^2} \approx 30, 01.$

Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента $а_{i}$ используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака " 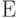" в расчетную формулу (11.2) подставляется десятичное число .

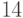Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления - самым старшим разрядом в новой записи числа.

Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.

Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).

$\arraycolsep=0.05em \begin{array}{l@{\,}rl@{\,}rl@{\,}rl@{\,}rl@{\,}rl@{\,}rl@{\,}rl} &_{-}125 &\|2 &&&&&\\ \cline{3-4} &124 &&_{-}62 &\|2\\ \cline{2-2}\cline{5-6} &1 & &62 &&_{-}31 &\|2\\ \cline{4-4}\cline{7-8} &&&0 & &30 &&_{-}15 &\|2\\ \cline{6-6}\cline{9-10} & && &&1 &&14 &&_{-}7 &\|2\\ \cline{8-8}\cline{11-12} &&&&&&&1&&6 &&_{-}3 &\|2\\ \cline{10-10}\cline{13-14} &&&&&&&&&1 &&2&&1\\ \cline{12-12} &&&&&&&&&&&1\\ \end{array} \\ 125_{10} = 1111101_2$	$\arraycolsep=0.05em \begin{array}{rrrrrrrr} _{-}&1&2&5&\|8\\ \cline{5-6} & &8& &_{-}&15&\|8\\ \cline{2-3}\cline{7-7} &_{-}&4&5& & 8& 1\\ \cline{6-6} & &4&0& & 7\\ \cline{3-4} & & &5 \end{array} \\ 125_{10}=175_8$	$\arraycolsep=0.05em \begin{array}{rrr} _{-} & 125 & \|16\\ \cline{3-3} & 112 & 7\\ \cline{2-2} & 13\\ \end{array} \\ 125_{10} = 7D_{16}$
a)	б)	в)

Проверка:

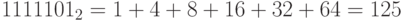в двоичном коде: $1111101_{2}= 1+4+8+16+32+64=125$ ;
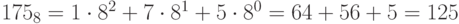в восьмеричном коде $175_{8} = 1\cdot 8^{2 }+ 7\cdot 8^{1} + 5\cdot 8^{0} = 64+56+5=125$ ;
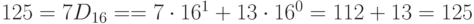в шестнадцатеричном коде - $125 = 7D_{16} = =7\cdot 16^{1} + 13\cdot 16^{0} = 112 + 13 = 125$ .

В рассмотренном примере при переводе вместо коэффициента $а_{0} =D$ используется его десятичный эквивалент 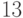в соответствии с таблицей 11.2.

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.

Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).

Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Примеры:

перевод в шестнадцатеричную систему:
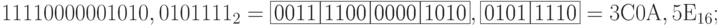
$11110000001010,0101111_{2}=\fbox{0011} \fbox{1100} \fbox{0000} \fbox{1010} , \fbox{0101} \fbox{1110} = 3С0А, 5Е_{16};$
перевод в восьмеричную систему:
$1100000110,10111_{2}=\fbox{001} \fbox{100 }\fbox{000}\fbox{ 110 }, \fbox{101 }\fbox{110 }= 1406, 56_{8}.$

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже - в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.

Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).

Примеры:

для шестнадцатеричного числа: $127, В6_{16 }= 000100100111,10110110_{2} = 100100111,1011011_{2}$ ;
для восьмеричного числа: $147,554_{8} = 001100111,101101100_{2 }= 1100111,1011011_{2}$ .

Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.

Дальше >>

Основы цифровой техники

Основы цифровой техники

Двоичные числа и двоичная арифметика

Принцип представления чисел в позиционных системах счисления

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Вопросы и ответы

Студенты

Авторизоваться

Основы цифровой техники

Основы цифровой техники

Двоичные числа и двоичная арифметика

Принцип представления чисел в позиционных системах счисления

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Вопросы и ответы

Студенты